Cameron Musco
Efficient Intervention Design for Causal Discovery with Latents
May 24, 2020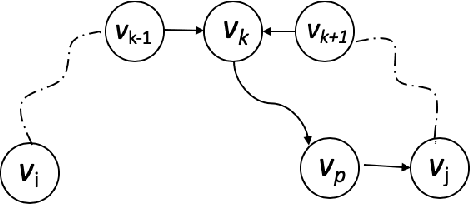
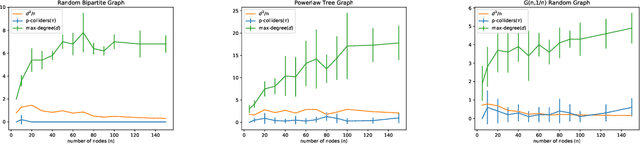
Abstract:We consider recovering a causal graph in presence of latent variables, where we seek to minimize the cost of interventions used in the recovery process. We consider two intervention cost models: (1) a linear cost model where the cost of an intervention on a subset of variables has a linear form, and (2) an identity cost model where the cost of an intervention is the same, regardless of what variables it is on, i.e., the goal is just to minimize the number of interventions. Under the linear cost model, we give an algorithm to identify the ancestral relations of the underlying causal graph, achieving within a $2$-factor of the optimal intervention cost. This approximation factor can be improved to $1+\epsilon$ for any $\epsilon > 0$ under some mild restrictions. Under the identity cost model, we bound the number of interventions needed to recover the entire causal graph, including the latent variables, using a parameterization of the causal graph through a special type of colliders. In particular, we introduce the notion of $p$-colliders, that are colliders between pair of nodes arising from a specific type of conditioning in the causal graph, and provide an upper bound on the number of interventions as a function of the maximum number of $p$-colliders between any two nodes in the causal graph.
Projection-Cost-Preserving Sketches: Proof Strategies and Constructions
Apr 17, 2020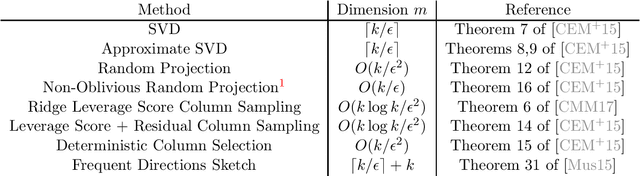
Abstract:In this note we illustrate how common matrix approximation methods, such as random projection and random sampling, yield projection-cost-preserving sketches, as introduced in [FSS13, CEM+15]. A projection-cost-preserving sketch is a matrix approximation which, for a given parameter $k$, approximately preserves the distance of the target matrix to all $k$-dimensional subspaces. Such sketches have applications to scalable algorithms for linear algebra, data science, and machine learning. Our goal is to simplify the presentation of proof techniques introduced in [CEM+15] and [CMM17] so that they can serve as a guide for future work. We also refer the reader to [CYD19], which gives a similar simplified exposition of the proof covered in Section 2.
Importance Sampling via Local Sensitivity
Nov 04, 2019
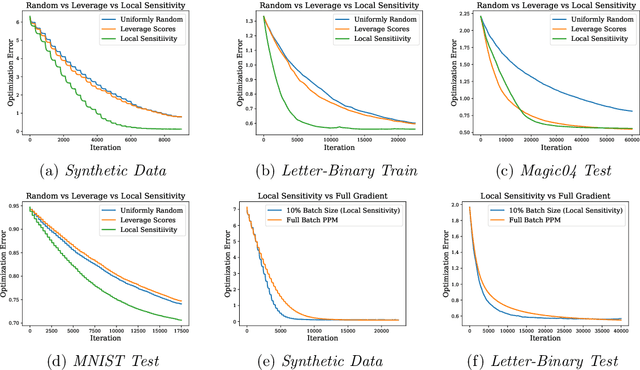
Abstract:Given a loss function $F:\mathcal{X} \rightarrow \mathbb{R}^+$ that can be written as the sum of losses over a large set of inputs $a_1,\ldots, a_n$, it is often desirable to approximate $F$ by subsampling the input points. Strong theoretical guarantees require taking into account the importance of each point, measured by how much its individual loss contributes to $F(x)$. Maximizing this importance over all $x \in \mathcal{X}$ yields the \emph{sensitivity score} of $a_i$. Sampling with probabilities proportional to these scores gives strong provable guarantees, allowing one to approximately minimize of $F$ using just the subsampled points. Unfortunately, sensitivity sampling is difficult to apply since 1) it is unclear how to efficiently compute the sensitivity scores and 2) the sample size required is often too large to be useful. We propose overcoming both obstacles by introducing the \emph{local sensitivity}, which measures data point importance in a ball around some center $x_0$. We show that the local sensitivity can be efficiently estimated using the \emph{leverage scores} of a quadratic approximation to $F$, and that the sample size required to approximate $F$ around $x_0$ can be bounded. We propose employing local sensitivity sampling in an iterative optimization method and illustrate its usefulness by analyzing its convergence when $F$ is smooth and convex.
Toward a Characterization of Loss Functions for Distribution Learning
Jun 06, 2019

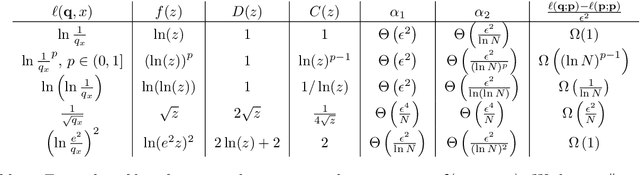
Abstract:In this work we study loss functions for learning and evaluating probability distributions over large discrete domains. Unlike classification or regression where a wide variety of loss functions are used, in the distribution learning and density estimation literature, very few losses outside the dominant $log\ loss$ are applied. We aim to understand this fact, taking an axiomatic approach to the design of loss functions for learning distributions. We start by proposing a set of desirable criteria that any good loss function should satisfy. Intuitively, these criteria require that the loss function faithfully evaluates a candidate distribution, both in expectation and when estimated on a few samples. Interestingly, we observe that \emph{no loss function} possesses all of these criteria. However, one can circumvent this issue by introducing a natural restriction on the set of candidate distributions. Specifically, we require that candidates are $calibrated$ with respect to the target distribution, i.e., they may contain less information than the target but otherwise do not significantly distort the truth. We show that, after restricting to this set of distributions, the log loss, along with a large variety of other losses satisfy the desired criteria. These results pave the way for future investigations of distribution learning that look beyond the log loss, choosing a loss function based on application or domain need.
Sample Efficient Toeplitz Covariance Estimation
Jun 06, 2019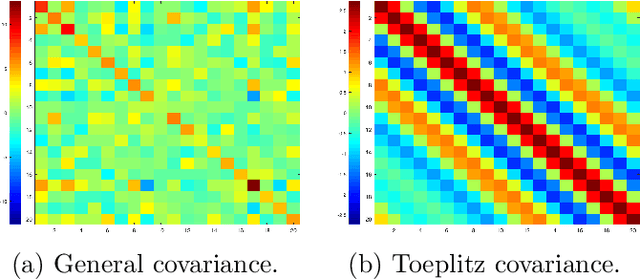
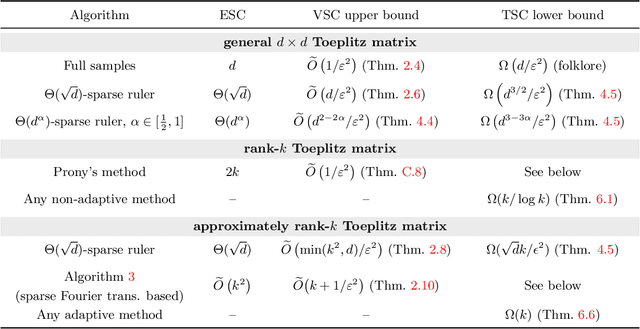
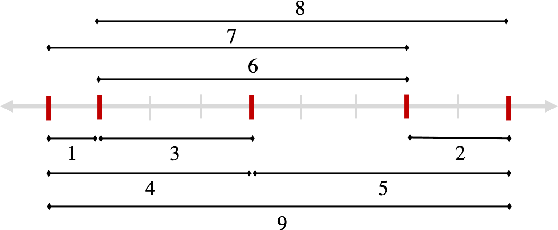
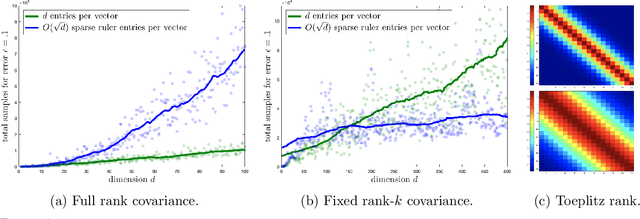
Abstract:We study the sample complexity of estimating the covariance matrix $T$ of a distribution $\mathcal{D}$ over $d$-dimensional vectors, under the assumption that $T$ is Toeplitz. This assumption arises in many signal processing problems, where the covariance between any two measurements only depends on the time or distance between those measurements. We are interested in estimation strategies that may choose to view only a subset of entries in each vector sample $x \sim \mathcal{D}$, which often equates to reducing hardware and communication requirements in applications ranging from wireless signal processing to advanced imaging. Our goal is to minimize both 1) the number of vector samples drawn from $\mathcal{D}$ and 2) the number of entries accessed in each sample. We provide some of the first non-asymptotic bounds on these sample complexity measures that exploit $T$'s Toeplitz structure, and by doing so, significantly improve on results for generic covariance matrices. Our bounds follow from a novel analysis of classical and widely used estimation algorithms (along with some new variants), including methods based on selecting entries from each vector sample according to a so-called sparse ruler. In many cases, we pair our upper bounds with matching or nearly matching lower bounds. In addition to results that hold for any Toeplitz $T$, we further study the important setting when $T$ is close to low-rank, which is often the case in practice. We show that methods based on sparse rulers perform even better in this setting, with sample complexity scaling sublinearly in $d$. Motivated by this finding, we develop a new covariance estimation strategy that further improves on all existing methods in the low-rank case: when $T$ is rank-$k$ or nearly rank-$k$, it achieves sample complexity depending polynomially on $k$ and only logarithmically on $d$.
Learning to Prune: Speeding up Repeated Computations
Apr 26, 2019
Abstract:It is common to encounter situations where one must solve a sequence of similar computational problems. Running a standard algorithm with worst-case runtime guarantees on each instance will fail to take advantage of valuable structure shared across the problem instances. For example, when a commuter drives from work to home, there are typically only a handful of routes that will ever be the shortest path. A naive algorithm that does not exploit this common structure may spend most of its time checking roads that will never be in the shortest path. More generally, we can often ignore large swaths of the search space that will likely never contain an optimal solution. We present an algorithm that learns to maximally prune the search space on repeated computations, thereby reducing runtime while provably outputting the correct solution each period with high probability. Our algorithm employs a simple explore-exploit technique resembling those used in online algorithms, though our setting is quite different. We prove that, with respect to our model of pruning search spaces, our approach is optimal up to constant factors. Finally, we illustrate the applicability of our model and algorithm to three classic problems: shortest-path routing, string search, and linear programming. We present experiments confirming that our simple algorithm is effective at significantly reducing the runtime of solving repeated computations.
Winner-Take-All Computation in Spiking Neural Networks
Apr 25, 2019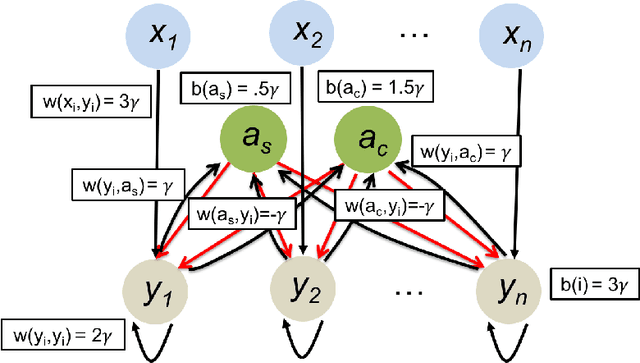

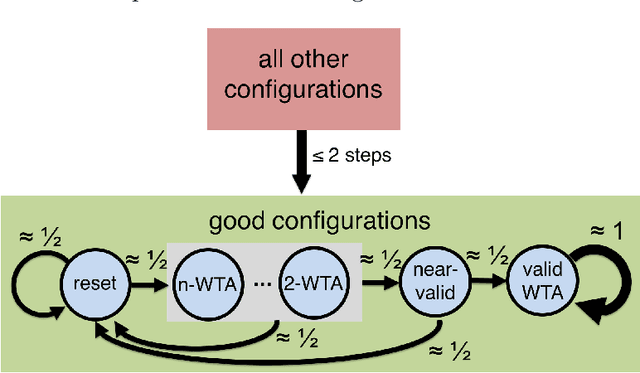
Abstract:In this work we study biological neural networks from an algorithmic perspective, focusing on understanding tradeoffs between computation time and network complexity. Our goal is to abstract real neural networks in a way that, while not capturing all interesting features, preserves high-level behavior and allows us to make biologically relevant conclusions. Towards this goal, we consider the implementation of algorithmic primitives in a simple yet biologically plausible model of $stochastic\ spiking\ neural\ networks$. In particular, we show how the stochastic behavior of neurons in this model can be leveraged to solve a basic $symmetry-breaking\ task$ in which we are given neurons with identical firing rates and want to select a distinguished one. In computational neuroscience, this is known as the winner-take-all (WTA) problem, and it is believed to serve as a basic building block in many tasks, e.g., learning, pattern recognition, and clustering. We provide efficient constructions of WTA circuits in our stochastic spiking neural network model, as well as lower bounds in terms of the number of auxiliary neurons required to drive convergence to WTA in a given number of steps. These lower bounds demonstrate that our constructions are near-optimal in some cases. This work covers and gives more in-depth proofs of a subset of results originally published in [LMP17a]. It is adapted from the last chapter of C. Musco's Ph.D. thesis [Mus18].
Low-Rank Approximation from Communication Complexity
Apr 22, 2019
Abstract:In low-rank approximation with missing entries, given $A\in \mathbb{R}^{n\times n}$ and binary $W \in \{0,1\}^{n\times n}$, the goal is to find a rank-$k$ matrix $L$ for which: $$cost(L)=\sum_{i=1}^{n} \sum_{j=1}^{n}W_{i,j}\cdot (A_{i,j} - L_{i,j})^2\le OPT+\epsilon \|A\|_F^2,$$ where $OPT=\min_{rank-k\ \hat{L}}cost(\hat L)$. This problem is also known as matrix completion and, depending on the choice of $W$, captures low-rank plus diagonal decomposition, robust PCA, low-rank recovery from monotone missing data, and a number of other important problems. Many of these problems are NP-hard, and while algorithms with provable guarantees are known in some cases, they either 1) run in time $n^{\Omega(k^2/\epsilon)}$, or 2) make strong assumptions, e.g., that $A$ is incoherent or that $W$ is random. In this work, we consider $bicriteria\ algorithms$, which output $L$ with rank $k' > k$. We prove that a common heuristic, which simply sets $A$ to $0$ where $W$ is $0$, and then computes a standard low-rank approximation, achieves the above approximation bound with rank $k'$ depending on the $communication\ complexity$ of $W$. Namely, interpreting $W$ as the communication matrix of a Boolean function $f(x,y)$ with $x,y\in \{0,1\}^{\log n}$, it suffices to set $k'=O(k\cdot 2^{R^{1-sided}_{\epsilon}(f)})$, where $R^{1-sided}_{\epsilon}(f)$ is the randomized communication complexity of $f$ with $1$-sided error probability $\epsilon$. For many problems, this yields bicriteria algorithms with $k'=k\cdot poly((\log n)/\epsilon)$. We prove a similar bound using the randomized communication complexity with $2$-sided error. Further, we show that different models of communication yield algorithms for natural variants of the problem. E.g., multi-player communication complexity connects to tensor decomposition and non-deterministic communication complexity to Boolean low-rank factorization.
A Universal Sampling Method for Reconstructing Signals with Simple Fourier Transforms
Dec 20, 2018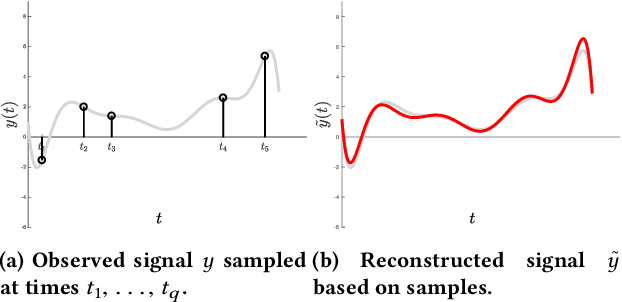

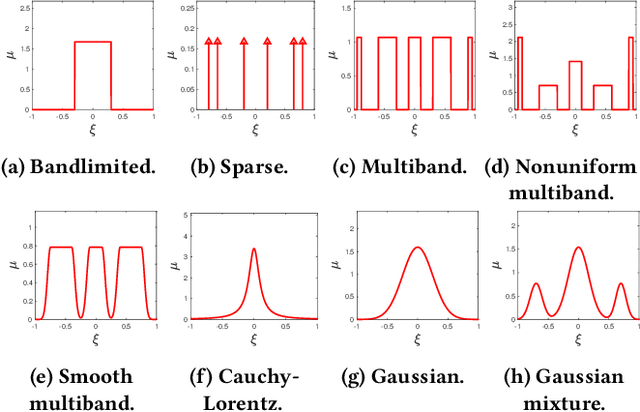
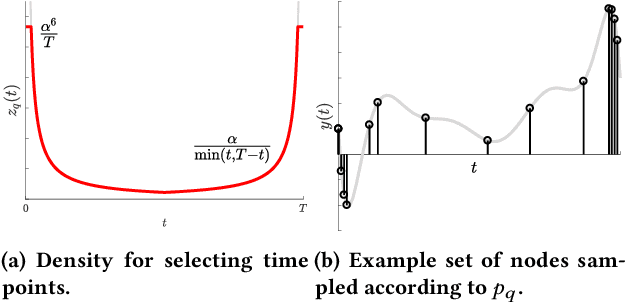
Abstract:Reconstructing continuous signals from a small number of discrete samples is a fundamental problem across science and engineering. In practice, we are often interested in signals with 'simple' Fourier structure, such as bandlimited, multiband, and Fourier sparse signals. More broadly, any prior knowledge about a signal's Fourier power spectrum can constrain its complexity. Intuitively, signals with more highly constrained Fourier structure require fewer samples to reconstruct. We formalize this intuition by showing that, roughly, a continuous signal from a given class can be approximately reconstructed using a number of samples proportional to the *statistical dimension* of the allowed power spectrum of that class. Further, in nearly all settings, this natural measure tightly characterizes the sample complexity of signal reconstruction. Surprisingly, we also show that, up to logarithmic factors, a universal non-uniform sampling strategy can achieve this optimal complexity for *any class of signals*. We present a simple and efficient algorithm for recovering a signal from the samples taken. For bandlimited and sparse signals, our method matches the state-of-the-art. At the same time, it gives the first computationally and sample efficient solution to a broad range of problems, including multiband signal reconstruction and kriging and Gaussian process regression tasks in one dimension. Our work is based on a novel connection between randomized linear algebra and signal reconstruction with constrained Fourier structure. We extend tools based on statistical leverage score sampling and column-based matrix reconstruction to the approximation of continuous linear operators that arise in signal reconstruction. We believe that these extensions are of independent interest and serve as a foundation for tackling a broad range of continuous time problems using randomized methods.
A Basic Compositional Model for Spiking Neural Networks
Aug 12, 2018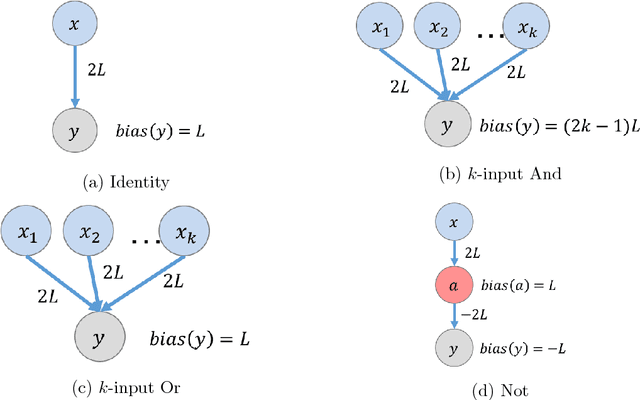
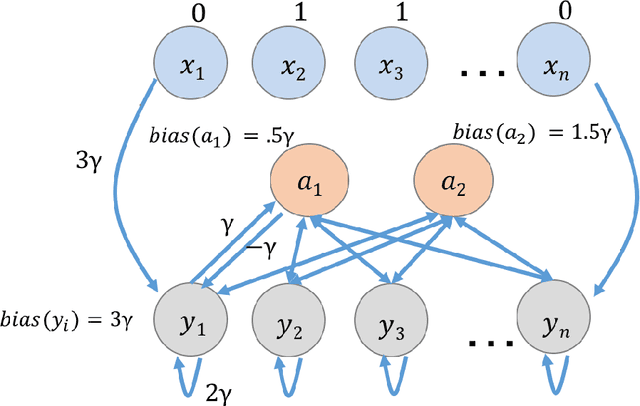
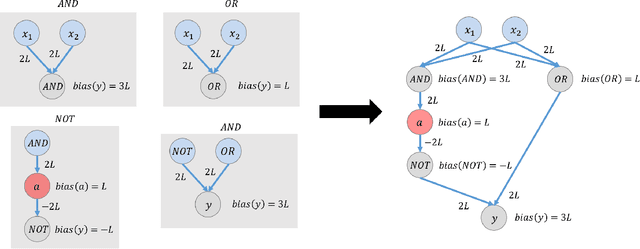
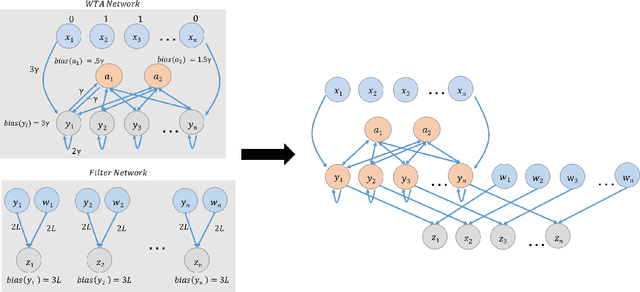
Abstract:This paper is part of a project on developing an algorithmic theory of brain networks, based on stochastic Spiking Neural Network (SNN) models. Inspired by tasks that seem to be solved in actual brains, we are defining abstract problems to be solved by these networks. In our work so far, we have developed models and algorithms for the Winner-Take-All problem from computational neuroscience [LMP17a,Mus18], and problems of similarity detection and neural coding [LMP17b]. We plan to consider many other problems and networks, including both static networks and networks that learn. This paper is about basic theory for the stochastic SNN model. In particular, we define a simple version of the model. This version assumes that the neurons' only state is a Boolean, indicating whether the neuron is firing or not. In later work, we plan to develop variants of the model with more elaborate state. We also define an external behavior notion for SNNs, which can be used for stating requirements to be satisfied by the networks. We then define a composition operator for SNNs. We prove that our external behavior notion is "compositional", in the sense that the external behavior of a composed network depends only on the external behaviors of the component networks. We also define a hiding operator that reclassifies some output behavior of an SNN as internal. We give basic results for hiding. Finally, we give a formal definition of a problem to be solved by an SNN, and give basic results showing how composition and hiding of networks affect the problems that they solve. We illustrate our definitions with three examples: building a circuit out of gates, building an "Attention" network out of a "Winner-Take-All" network and a "Filter" network, and a toy example involving combining two networks in a cyclic fashion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge