Multivariate trace estimation using quantum state space linear algebra

In this paper, we present a quantum algorithm for approximating multivariate traces, i.e. the traces of matrix products. Our research is motivated by the extensive utility of multivariate traces in elucidating spectral characteristics of matrices, as well as by recent advancements in leveraging quantum computing for faster numerical linear algebra. Central to our approach is a direct translation of a multivariate trace formula into a quantum circuit, achieved through a sequence of low-level circuit construction operations. To facilitate this translation, we introduce \emph{quantum Matrix States Linear Algebra} (qMSLA), a framework tailored for the efficient generation of state preparation circuits via primitive matrix algebra operations. Our algorithm relies on sets of state preparation circuits for input matrices as its primary inputs and yields two state preparation circuits encoding the multivariate trace as output. These circuits are constructed utilizing qMSLA operations, which enact the aforementioned multivariate trace formula. We emphasize that our algorithm's inputs consist solely of state preparation circuits, eschewing harder to synthesize constructs such as Block Encodings. Furthermore, our approach operates independently of the availability of specialized hardware like QRAM, underscoring its versatility and practicality.

On the Role of Initialization on the Implicit Bias in Deep Linear Networks

Despite Deep Learning's (DL) empirical success, our theoretical understanding of its efficacy remains limited. One notable paradox is that while conventional wisdom discourages perfect data fitting, deep neural networks are designed to do just that, yet they generalize effectively. This study focuses on exploring this phenomenon attributed to the implicit bias at play. Various sources of implicit bias have been identified, such as step size, weight initialization, optimization algorithm, and number of parameters. In this work, we focus on investigating the implicit bias originating from weight initialization. To this end, we examine the problem of solving underdetermined linear systems in various contexts, scrutinizing the impact of initialization on the implicit regularization when using deep networks to solve such systems. Our findings elucidate the role of initialization in the optimization and generalization paradoxes, contributing to a more comprehensive understanding of DL's performance characteristics.

Manifold Free Riemannian Optimization

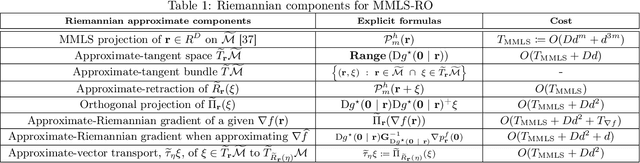
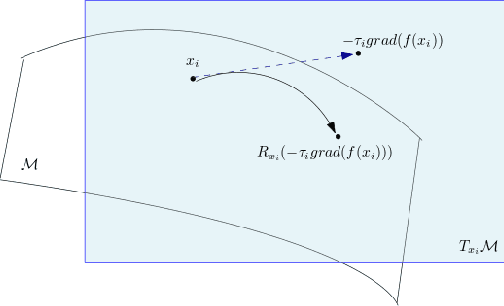
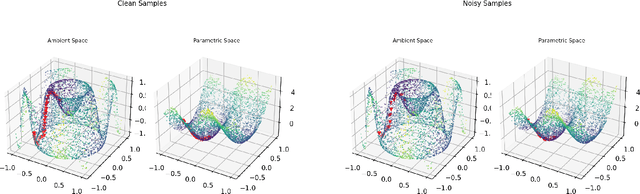
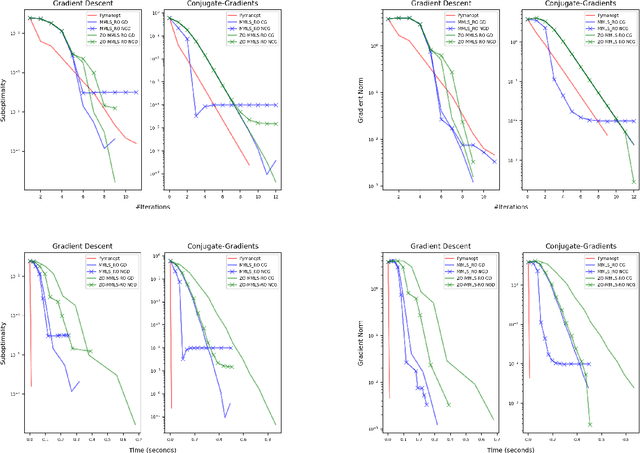
Riemannian optimization is a principled framework for solving optimization problems where the desired optimum is constrained to a smooth manifold $\mathcal{M}$. Algorithms designed in this framework usually require some geometrical description of the manifold, which typically includes tangent spaces, retractions, and gradients of the cost function. However, in many cases, only a subset (or none at all) of these elements can be accessed due to lack of information or intractability. In this paper, we propose a novel approach that can perform approximate Riemannian optimization in such cases, where the constraining manifold is a submanifold of $\R^{D}$. At the bare minimum, our method requires only a noiseless sample set of the cost function $(\x_{i}, y_{i})\in {\mathcal{M}} \times \mathbb{R}$ and the intrinsic dimension of the manifold $\mathcal{M}$. Using the samples, and utilizing the Manifold-MLS framework (Sober and Levin 2020), we construct approximations of the missing components entertaining provable guarantees and analyze their computational costs. In case some of the components are given analytically (e.g., if the cost function and its gradient are given explicitly, or if the tangent spaces can be computed), the algorithm can be easily adapted to use the accurate expressions instead of the approximations. We analyze the global convergence of Riemannian gradient-based methods using our approach, and we demonstrate empirically the strength of this method, together with a conjugate-gradients type method based upon similar principles.

Near Optimal Reconstruction of Spherical Harmonic Expansions

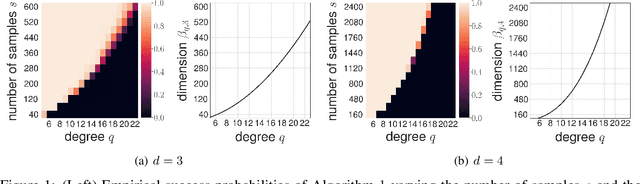
We propose an algorithm for robust recovery of the spherical harmonic expansion of functions defined on the d-dimensional unit sphere $\mathbb{S}^{d-1}$ using a near-optimal number of function evaluations. We show that for any $f \in L^2(\mathbb{S}^{d-1})$, the number of evaluations of $f$ needed to recover its degree-$q$ spherical harmonic expansion equals the dimension of the space of spherical harmonics of degree at most $q$ up to a logarithmic factor. Moreover, we develop a simple yet efficient algorithm to recover degree-$q$ expansion of $f$ by only evaluating the function on uniformly sampled points on $\mathbb{S}^{d-1}$. Our algorithm is based on the connections between spherical harmonics and Gegenbauer polynomials and leverage score sampling methods. Unlike the prior results on fast spherical harmonic transform, our proposed algorithm works efficiently using a nearly optimal number of samples in any dimension d. We further illustrate the empirical performance of our algorithm on numerical examples.

PCENet: High Dimensional Surrogate Modeling for Learning Uncertainty

Learning data representations under uncertainty is an important task that emerges in numerous machine learning applications. However, uncertainty quantification (UQ) techniques are computationally intensive and become prohibitively expensive for high-dimensional data. In this paper, we present a novel surrogate model for representation learning and uncertainty quantification, which aims to deal with data of moderate to high dimensions. The proposed model combines a neural network approach for dimensionality reduction of the (potentially high-dimensional) data, with a surrogate model method for learning the data distribution. We first employ a variational autoencoder (VAE) to learn a low-dimensional representation of the data distribution. We then propose to harness polynomial chaos expansion (PCE) formulation to map this distribution to the output target. The coefficients of PCE are learned from the distribution representation of the training data using a maximum mean discrepancy (MMD) approach. Our model enables us to (a) learn a representation of the data, (b) estimate uncertainty in the high-dimensional data system, and (c) match high order moments of the output distribution; without any prior statistical assumptions on the data. Numerical experimental results are presented to illustrate the performance of the proposed method.

Random Gegenbauer Features for Scalable Kernel Methods

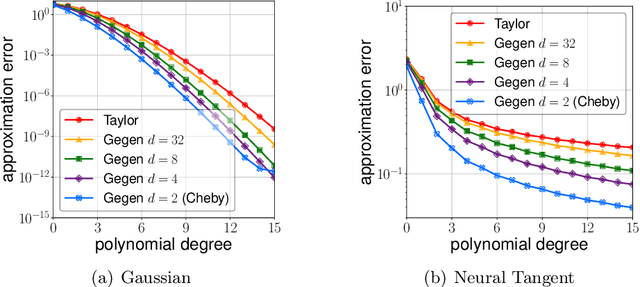
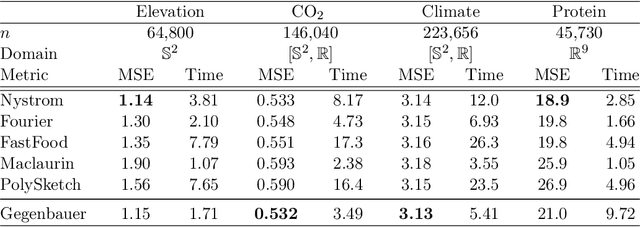
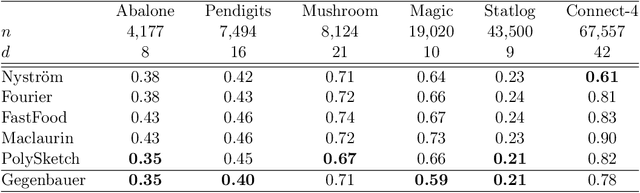
We propose efficient random features for approximating a new and rich class of kernel functions that we refer to as Generalized Zonal Kernels (GZK). Our proposed GZK family, generalizes the zonal kernels (i.e., dot-product kernels on the unit sphere) by introducing radial factors in their Gegenbauer series expansion, and includes a wide range of ubiquitous kernel functions such as the entirety of dot-product kernels as well as the Gaussian and the recently introduced Neural Tangent kernels. Interestingly, by exploiting the reproducing property of the Gegenbauer polynomials, we can construct efficient random features for the GZK family based on randomly oriented Gegenbauer kernels. We prove subspace embedding guarantees for our Gegenbauer features which ensures that our features can be used for approximately solving learning problems such as kernel k-means clustering, kernel ridge regression, etc. Empirical results show that our proposed features outperform recent kernel approximation methods.

Low-Rank Updates of Matrix Square Roots

Models in which the covariance matrix has the structure of a sparse matrix plus a low rank perturbation are ubiquitous in machine learning applications. It is often desirable for learning algorithms to take advantage of such structures, avoiding costly matrix computations that often require cubic time and quadratic storage. This is often accomplished by performing operations that maintain such structures, e.g. matrix inversion via the Sherman-Morrison-Woodbury formula. In this paper we consider the matrix square root and inverse square root operations. Given a low rank perturbation to a matrix, we argue that a low-rank approximate correction to the (inverse) square root exists. We do so by establishing a geometric decay bound on the true correction's eigenvalues. We then proceed to frame the correction has the solution of an algebraic Ricatti equation, and discuss how a low-rank solution to that equation can be computed. We analyze the approximation error incurred when approximately solving the algebraic Ricatti equation, providing spectral and Frobenius norm forward and backward error bounds. Finally, we describe several applications of our algorithms, and demonstrate their utility in numerical experiments.

Dimensionality Reduction of Longitudinal 'Omics Data using Modern Tensor Factorization

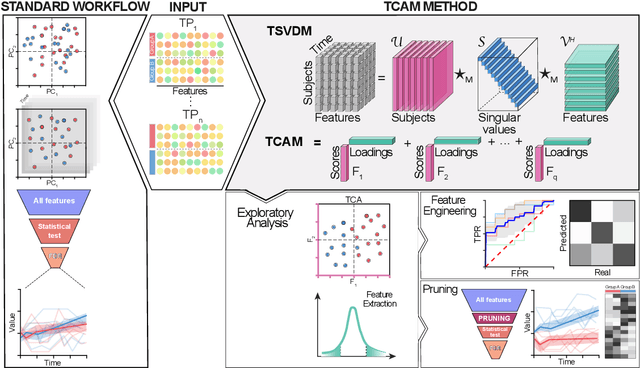
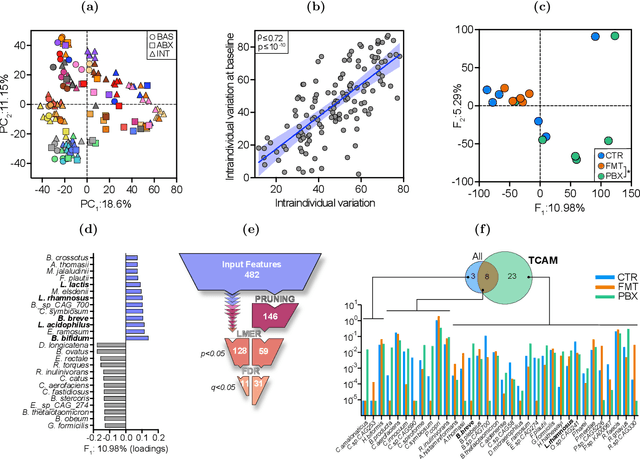
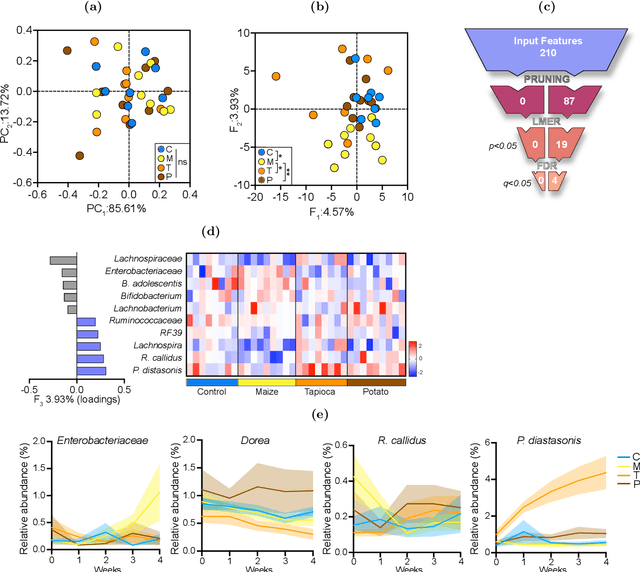
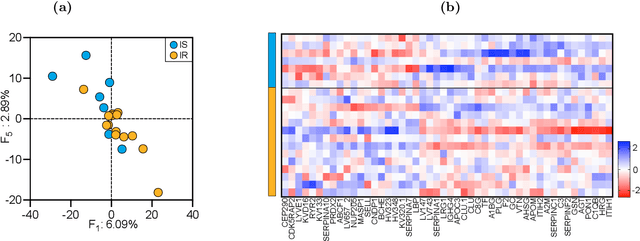
Precision medicine is a clinical approach for disease prevention, detection and treatment, which considers each individual's genetic background, environment and lifestyle. The development of this tailored avenue has been driven by the increased availability of omics methods, large cohorts of temporal samples, and their integration with clinical data. Despite the immense progression, existing computational methods for data analysis fail to provide appropriate solutions for this complex, high-dimensional and longitudinal data. In this work we have developed a new method termed TCAM, a dimensionality reduction technique for multi-way data, that overcomes major limitations when doing trajectory analysis of longitudinal omics data. Using real-world data, we show that TCAM outperforms traditional methods, as well as state-of-the-art tensor-based approaches for longitudinal microbiome data analysis. Moreover, we demonstrate the versatility of TCAM by applying it to several different omics datasets, and the applicability of it as a drop-in replacement within straightforward ML tasks.

Scaling Neural Tangent Kernels via Sketching and Random Features

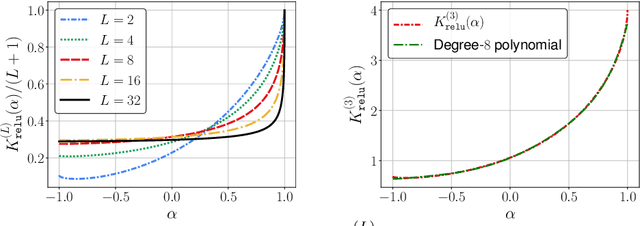
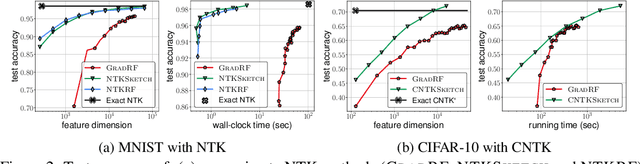
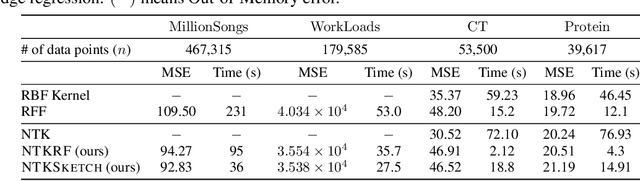
The Neural Tangent Kernel (NTK) characterizes the behavior of infinitely-wide neural networks trained under least squares loss by gradient descent. Recent works also report that NTK regression can outperform finitely-wide neural networks trained on small-scale datasets. However, the computational complexity of kernel methods has limited its use in large-scale learning tasks. To accelerate learning with NTK, we design a near input-sparsity time approximation algorithm for NTK, by sketching the polynomial expansions of arc-cosine kernels: our sketch for the convolutional counterpart of NTK (CNTK) can transform any image using a linear runtime in the number of pixels. Furthermore, we prove a spectral approximation guarantee for the NTK matrix, by combining random features (based on leverage score sampling) of the arc-cosine kernels with a sketching algorithm. We benchmark our methods on various large-scale regression and classification tasks and show that a linear regressor trained on our CNTK features matches the accuracy of exact CNTK on CIFAR-10 dataset while achieving 150x speedup.

Random Features for the Neural Tangent Kernel

The Neural Tangent Kernel (NTK) has discovered connections between deep neural networks and kernel methods with insights of optimization and generalization. Motivated by this, recent works report that NTK can achieve better performances compared to training neural networks on small-scale datasets. However, results under large-scale settings are hardly studied due to the computational limitation of kernel methods. In this work, we propose an efficient feature map construction of the NTK of fully-connected ReLU network which enables us to apply it to large-scale datasets. We combine random features of the arc-cosine kernels with a sketching-based algorithm which can run in linear with respect to both the number of data points and input dimension. We show that dimension of the resulting features is much smaller than other baseline feature map constructions to achieve comparable error bounds both in theory and practice. We additionally utilize the leverage score based sampling for improved bounds of arc-cosine random features and prove a spectral approximation guarantee of the proposed feature map to the NTK matrix of two-layer neural network. We benchmark a variety of machine learning tasks to demonstrate the superiority of the proposed scheme. In particular, our algorithm can run tens of magnitude faster than the exact kernel methods for large-scale settings without performance loss.