Trading off Consistency and Dimensionality of Convex Surrogates for the Mode

In multiclass classification over $n$ outcomes, the outcomes must be embedded into the reals with dimension at least $n-1$ in order to design a consistent surrogate loss that leads to the "correct" classification, regardless of the data distribution. For large $n$, such as in information retrieval and structured prediction tasks, optimizing a surrogate in $n-1$ dimensions is often intractable. We investigate ways to trade off surrogate loss dimension, the number of problem instances, and restricting the region of consistency in the simplex for multiclass classification. Following past work, we examine an intuitive embedding procedure that maps outcomes into the vertices of convex polytopes in a low-dimensional surrogate space. We show that full-dimensional subsets of the simplex exist around each point mass distribution for which consistency holds, but also, with less than $n-1$ dimensions, there exist distributions for which a phenomenon called hallucination occurs, which is when the optimal report under the surrogate loss is an outcome with zero probability. Looking towards application, we derive a result to check if consistency holds under a given polytope embedding and low-noise assumption, providing insight into when to use a particular embedding. We provide examples of embedding $n = 2^{d}$ outcomes into the $d$-dimensional unit cube and $n = d!$ outcomes into the $d$-dimensional permutahedron under low-noise assumptions. Finally, we demonstrate that with multiple problem instances, we can learn the mode with $\frac{n}{2}$ dimensions over the whole simplex.

Forecasting Competitions with Correlated Events

Beginning with Witkowski et al. [2022], recent work on forecasting competitions has addressed incentive problems with the common winner-take-all mechanism. Frongillo et al. [2021] propose a competition mechanism based on follow-the-regularized-leader (FTRL), an online learning framework. They show that their mechanism selects an $\epsilon$-optimal forecaster with high probability using only $O(\log(n)/\epsilon^2)$ events. These works, together with all prior work on this problem thus far, assume that events are independent. We initiate the study of forecasting competitions for correlated events. To quantify correlation, we introduce a notion of block correlation, which allows each event to be strongly correlated with up to $b$ others. We show that under distributions with this correlation, the FTRL mechanism retains its $\epsilon$-optimal guarantee using $O(b^2 \log(n)/\epsilon^2)$ events. Our proof involves a novel concentration bound for correlated random variables which may be of broader interest.

Proper losses for discrete generative models

We initiate the study of proper losses for evaluating generative models in the discrete setting. Unlike traditional proper losses, we treat both the generative model and the target distribution as black-boxes, only assuming ability to draw i.i.d. samples. We define a loss to be black-box proper if the generative distribution that minimizes expected loss is equal to the target distribution. Using techniques from statistical estimation theory, we give a general construction and characterization of black-box proper losses: they must take a polynomial form, and the number of draws from the model and target distribution must exceed the degree of the polynomial. The characterization rules out a loss whose expectation is the cross-entropy between the target distribution and the model. By extending the construction to arbitrary sampling schemes such as Poisson sampling, however, we show that one can construct such a loss.

An Embedding Framework for the Design and Analysis of Consistent Polyhedral Surrogates

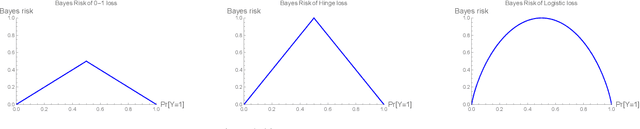
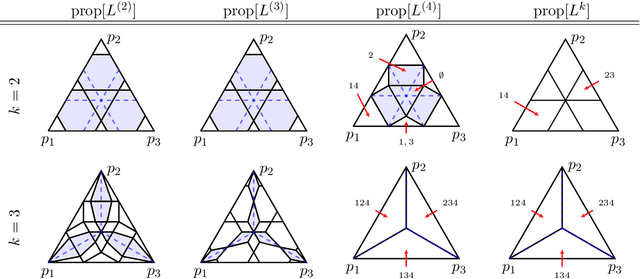
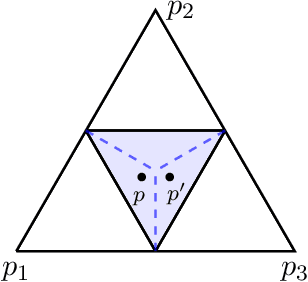
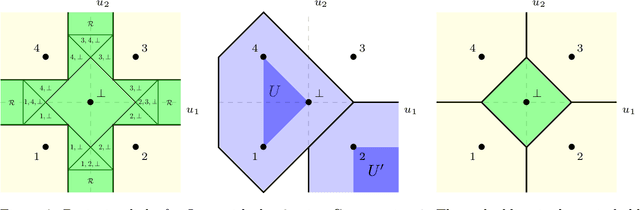
We formalize and study the natural approach of designing convex surrogate loss functions via embeddings, for problems such as classification, ranking, or structured prediction. In this approach, one embeds each of the finitely many predictions (e.g. rankings) as a point in $R^d$, assigns the original loss values to these points, and "convexifies" the loss in some way to obtain a surrogate. We establish a strong connection between this approach and polyhedral (piecewise-linear convex) surrogate losses: every discrete loss is embedded by some polyhedral loss, and every polyhedral loss embeds some discrete loss. Moreover, an embedding gives rise to a consistent link function as well as linear surrogate regret bounds. Our results are constructive, as we illustrate with several examples. In particular, our framework gives succinct proofs of consistency or inconsistency for various polyhedral surrogates in the literature, and for inconsistent surrogates, it further reveals the discrete losses for which these surrogates are consistent. We go on to show additional structure of embeddings, such as the equivalence of embedding and matching Bayes risks, and the equivalence of various notions of non-redudancy. Using these results, we establish that indirect elicitation, a necessary condition for consistency, is also sufficient when working with polyhedral surrogates.

Surrogate Regret Bounds for Polyhedral Losses

Surrogate risk minimization is an ubiquitous paradigm in supervised machine learning, wherein a target problem is solved by minimizing a surrogate loss on a dataset. Surrogate regret bounds, also called excess risk bounds, are a common tool to prove generalization rates for surrogate risk minimization. While surrogate regret bounds have been developed for certain classes of loss functions, such as proper losses, general results are relatively sparse. We provide two general results. The first gives a linear surrogate regret bound for any polyhedral (piecewise-linear and convex) surrogate, meaning that surrogate generalization rates translate directly to target rates. The second shows that for sufficiently non-polyhedral surrogates, the regret bound is a square root, meaning fast surrogate generalization rates translate to slow rates for the target. Together, these results suggest polyhedral surrogates are optimal in many cases.

Efficient Competitions and Online Learning with Strategic Forecasters

Winner-take-all competitions in forecasting and machine-learning suffer from distorted incentives. Witkowskiet al. identified this problem and proposed ELF, a truthful mechanism to select a winner. We show that, from a pool of $n$ forecasters, ELF requires $\Theta(n\log n)$ events or test data points to select a near-optimal forecaster with high probability. We then show that standard online learning algorithms select an $\epsilon$-optimal forecaster using only $O(\log(n) / \epsilon^2)$ events, by way of a strong approximate-truthfulness guarantee. This bound matches the best possible even in the nonstrategic setting. We then apply these mechanisms to obtain the first no-regret guarantee for non-myopic strategic experts.

Unifying Lower Bounds on Prediction Dimension of Consistent Convex Surrogates

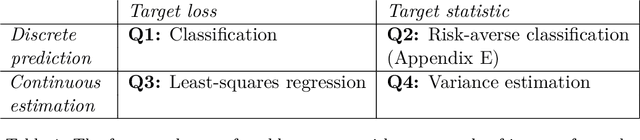
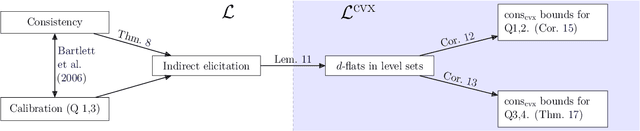
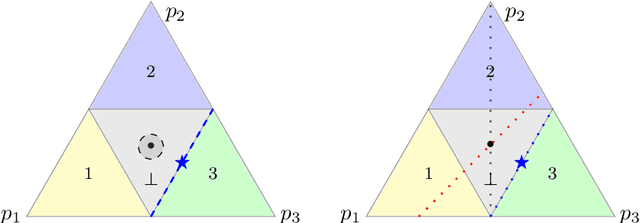
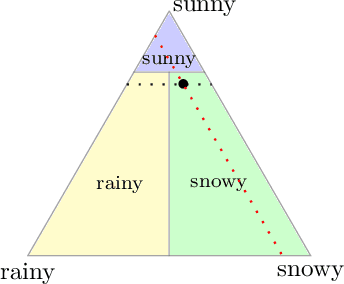
Given a prediction task, understanding when one can and cannot design a consistent convex surrogate loss, particularly a low-dimensional one, is an important and active area of machine learning research. The prediction task may be given as a target loss, as in classification and structured prediction, or simply as a (conditional) statistic of the data, as in risk measure estimation. These two scenarios typically involve different techniques for designing and analyzing surrogate losses. We unify these settings using tools from property elicitation, and give a general lower bound on prediction dimension. Our lower bound tightens existing results in the case of discrete predictions, showing that previous calibration-based bounds can largely be recovered via property elicitation. For continuous estimation, our lower bound resolves on open problem on estimating measures of risk and uncertainty.

Non-parametric Binary regression in metric spaces with KL loss

We propose a non-parametric variant of binary regression, where the hypothesis is regularized to be a Lipschitz function taking a metric space to [0,1] and the loss is logarithmic. This setting presents novel computational and statistical challenges. On the computational front, we derive a novel efficient optimization algorithm based on interior point methods; an attractive feature is that it is parameter-free (i.e., does not require tuning an update step size). On the statistical front, the unbounded loss function presents a problem for classic generalization bounds, based on covering-number and Rademacher techniques. We get around this challenge via an adaptive truncation approach, and also present a lower bound indicating that the truncation is, in some sense, necessary.

A Smoothed Analysis of Online Lasso for the Sparse Linear Contextual Bandit Problem

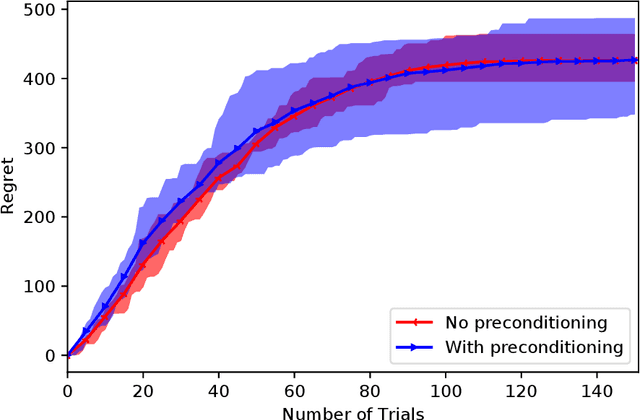
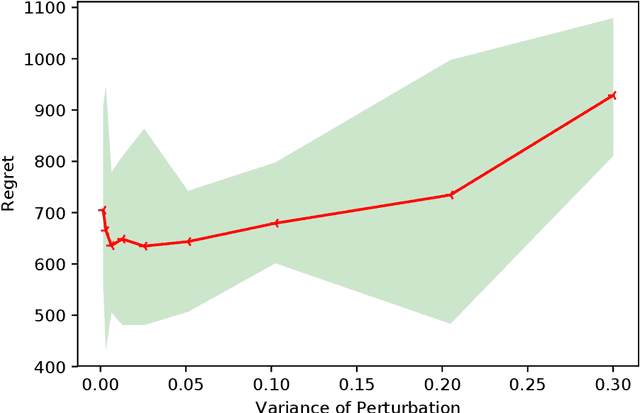
We investigate the sparse linear contextual bandit problem where the parameter $\theta$ is sparse. To relieve the sampling inefficiency, we utilize the "perturbed adversary" where the context is generated adversarilly but with small random non-adaptive perturbations. We prove that the simple online Lasso supports sparse linear contextual bandit with regret bound $\mathcal{O}(\sqrt{kT\log d})$ even when $d \gg T$ where $k$ and $d$ are the number of effective and ambient dimension, respectively. Compared to the recent work from Sivakumar et al. (2020), our analysis does not rely on the precondition processing, adaptive perturbation (the adaptive perturbation violates the i.i.d perturbation setting) or truncation on the error set. Moreover, the special structures in our results explicitly characterize how the perturbation affects exploration length, guide the design of perturbation together with the fundamental performance limit of perturbation method. Numerical experiments are provided to complement the theoretical analysis.

An Embedding Framework for Consistent Polyhedral Surrogates

We formalize and study the natural approach of designing convex surrogate loss functions via embeddings for problems such as classification or ranking. In this approach, one embeds each of the finitely many predictions (e.g. classes) as a point in R^d, assigns the original loss values to these points, and convexifies the loss in between to obtain a surrogate. We prove that this approach is equivalent, in a strong sense, to working with polyhedral (piecewise linear convex) losses. Moreover, given any polyhedral loss $L$, we give a construction of a link function through which $L$ is a consistent surrogate for the loss it embeds. We go on to illustrate the power of this embedding framework with succinct proofs of consistency or inconsistency of various polyhedral surrogates in the literature.