Artificial Intelligence Index Report 2024

The 2024 Index is our most comprehensive to date and arrives at an important moment when AI's influence on society has never been more pronounced. This year, we have broadened our scope to more extensively cover essential trends such as technical advancements in AI, public perceptions of the technology, and the geopolitical dynamics surrounding its development. Featuring more original data than ever before, this edition introduces new estimates on AI training costs, detailed analyses of the responsible AI landscape, and an entirely new chapter dedicated to AI's impact on science and medicine. The AI Index report tracks, collates, distills, and visualizes data related to artificial intelligence (AI). Our mission is to provide unbiased, rigorously vetted, broadly sourced data in order for policymakers, researchers, executives, journalists, and the general public to develop a more thorough and nuanced understanding of the complex field of AI. The AI Index is recognized globally as one of the most credible and authoritative sources for data and insights on artificial intelligence. Previous editions have been cited in major newspapers, including the The New York Times, Bloomberg, and The Guardian, have amassed hundreds of academic citations, and been referenced by high-level policymakers in the United States, the United Kingdom, and the European Union, among other places. This year's edition surpasses all previous ones in size, scale, and scope, reflecting the growing significance that AI is coming to hold in all of our lives.

Artificial Intelligence Index Report 2023

Welcome to the sixth edition of the AI Index Report. This year, the report introduces more original data than any previous edition, including a new chapter on AI public opinion, a more thorough technical performance chapter, original analysis about large language and multimodal models, detailed trends in global AI legislation records, a study of the environmental impact of AI systems, and more. The AI Index Report tracks, collates, distills, and visualizes data related to artificial intelligence. Our mission is to provide unbiased, rigorously vetted, broadly sourced data in order for policymakers, researchers, executives, journalists, and the general public to develop a more thorough and nuanced understanding of the complex field of AI. The report aims to be the world's most credible and authoritative source for data and insights about AI.

Generalization in the Face of Adaptivity: A Bayesian Perspective

Repeated use of a data sample via adaptively chosen queries can rapidly lead to overfitting, wherein the issued queries yield answers on the sample that differ wildly from the values of those queries on the underlying data distribution. Differential privacy provides a tool to ensure generalization despite adaptively-chosen queries, but its worst-case nature means that it cannot, for example, yield improved results for low-variance queries. In this paper, we give a simple new characterization that illuminates the core problem of adaptive data analysis. We show explicitly that the harms of adaptivity come from the covariance between the behavior of future queries and a Bayes factor-based measure of how much information about the data sample was encoded in the responses given to past queries. We leverage this intuition to introduce a new stability notion; we then use it to prove new generalization results for the most basic noise-addition mechanisms (Laplace and Gaussian noise addition), with guarantees that scale with the variance of the queries rather than the square of their range. Our characterization opens the door to new insights and new algorithms for the fundamental problem of achieving generalization in adaptive data analysis.

Causal Feature Discovery through Strategic Modification

We consider an online regression setting in which individuals adapt to the regression model: arriving individuals may access the model throughout the process, and invest strategically in modifying their own features so as to improve their assigned score. We find that this strategic manipulation may help a learner recover the causal variables, in settings where an agent can invest in improving impactful features that also improve his true label. We show that even simple behavior on the learner's part (i.e., periodically updating her model based on the observed data so far, via least-square regression) allows her to simultaneously i) accurately recover which features have an impact on an agent's true label, provided they have been invested in significantly, and ii) incentivize agents to invest in these impactful features, rather than in features that have no effect on their true label.

Learn to Expect the Unexpected: Probably Approximately Correct Domain Generalization

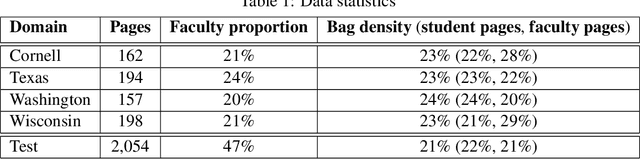
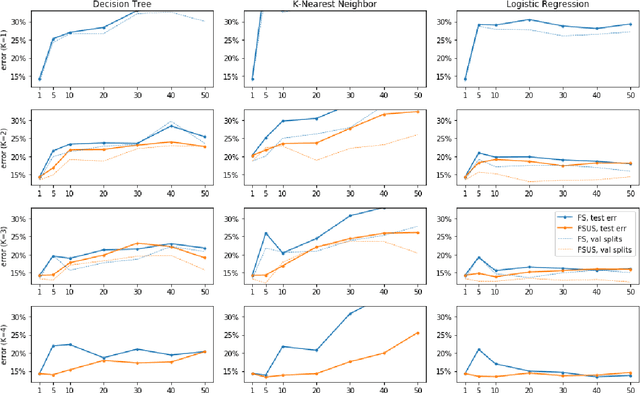
Domain generalization is the problem of machine learning when the training data and the test data come from different data domains. We present a simple theoretical model of learning to generalize across domains in which there is a meta-distribution over data distributions, and those data distributions may even have different supports. In our model, the training data given to a learning algorithm consists of multiple datasets each from a single domain drawn in turn from the meta-distribution. We study this model in three different problem settings---a multi-domain Massart noise setting, a decision tree multi-dataset setting, and a feature selection setting, and find that computationally efficient, polynomial-sample domain generalization is possible in each. Experiments demonstrate that our feature selection algorithm indeed ignores spurious correlations and improves generalization.

Privately Learning Thresholds: Closing the Exponential Gap

We study the sample complexity of learning threshold functions under the constraint of differential privacy. It is assumed that each labeled example in the training data is the information of one individual and we would like to come up with a generalizing hypothesis $h$ while guaranteeing differential privacy for the individuals. Intuitively, this means that any single labeled example in the training data should not have a significant effect on the choice of the hypothesis. This problem has received much attention recently; unlike the non-private case, where the sample complexity is independent of the domain size and just depends on the desired accuracy and confidence, for private learning the sample complexity must depend on the domain size $X$ (even for approximate differential privacy). Alon et al. (STOC 2019) showed a lower bound of $\Omega(\log^*|X|)$ on the sample complexity and Bun et al. (FOCS 2015) presented an approximate-private learner with sample complexity $\tilde{O}\left(2^{\log^*|X|}\right)$. In this work we reduce this gap significantly, almost settling the sample complexity. We first present a new upper bound (algorithm) of $\tilde{O}\left(\left(\log^*|X|\right)^2\right)$ on the sample complexity and then present an improved version with sample complexity $\tilde{O}\left(\left(\log^*|X|\right)^{1.5}\right)$. Our algorithm is constructed for the related interior point problem, where the goal is to find a point between the largest and smallest input elements. It is based on selecting an input-dependent hash function and using it to embed the database into a domain whose size is reduced logarithmically; this results in a new database, an interior point of which can be used to generate an interior point in the original database in a differentially private manner.

A New Analysis of Differential Privacy's Generalization Guarantees

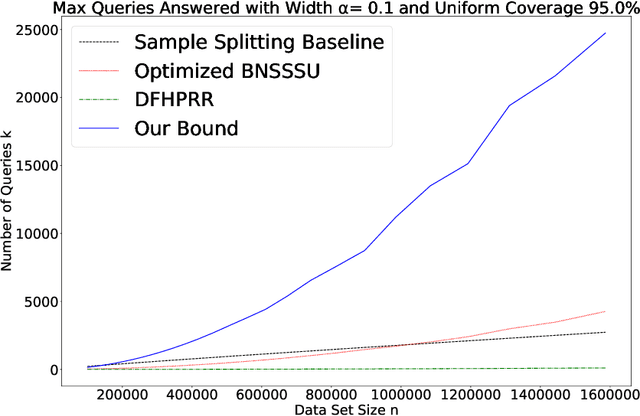
We give a new proof of the "transfer theorem" underlying adaptive data analysis: that any mechanism for answering adaptively chosen statistical queries that is differentially private and sample-accurate is also accurate out-of-sample. Our new proof is elementary and gives structural insights that we expect will be useful elsewhere. We show: 1) that differential privacy ensures that the expectation of any query on the posterior distribution on datasets induced by the transcript of the interaction is close to its true value on the data distribution, and 2) sample accuracy on its own ensures that any query answer produced by the mechanism is close to its posterior expectation with high probability. This second claim follows from a thought experiment in which we imagine that the dataset is resampled from the posterior distribution after the mechanism has committed to its answers. The transfer theorem then follows by summing these two bounds, and in particular, avoids the "monitor argument" used to derive high probability bounds in prior work. An upshot of our new proof technique is that the concrete bounds we obtain are substantially better than the best previously known bounds, even though the improvements are in the constants, rather than the asymptotics (which are known to be tight). As we show, our new bounds outperform the naive "sample-splitting" baseline at dramatically smaller dataset sizes compared to the previous state of the art, bringing techniques from this literature closer to practicality.

A necessary and sufficient stability notion for adaptive generalization

We introduce a new notion of the stability of computations, which holds under post-processing and adaptive composition, and show that the notion is both necessary and sufficient to ensure generalization in the face of adaptivity, for any computations that respond to bounded-sensitivity linear queries while providing accuracy with respect to the data sample set. The stability notion is based on quantifying the effect of observing a computation's outputs on the posterior over the data sample elements. We show a separation between this stability notion and previously studied notions.

Learning to Prune: Speeding up Repeated Computations

It is common to encounter situations where one must solve a sequence of similar computational problems. Running a standard algorithm with worst-case runtime guarantees on each instance will fail to take advantage of valuable structure shared across the problem instances. For example, when a commuter drives from work to home, there are typically only a handful of routes that will ever be the shortest path. A naive algorithm that does not exploit this common structure may spend most of its time checking roads that will never be in the shortest path. More generally, we can often ignore large swaths of the search space that will likely never contain an optimal solution. We present an algorithm that learns to maximally prune the search space on repeated computations, thereby reducing runtime while provably outputting the correct solution each period with high probability. Our algorithm employs a simple explore-exploit technique resembling those used in online algorithms, though our setting is quite different. We prove that, with respect to our model of pruning search spaces, our approach is optimal up to constant factors. Finally, we illustrate the applicability of our model and algorithm to three classic problems: shortest-path routing, string search, and linear programming. We present experiments confirming that our simple algorithm is effective at significantly reducing the runtime of solving repeated computations.

Equal Opportunity in Online Classification with Partial Feedback

We study an online classification problem with partial feedback in which individuals arrive one at a time from a fixed but unknown distribution, and must be classified as positive or negative. Our algorithm only observes the true label of an individual if they are given a positive classification. This setting captures many classification problems for which fairness is a concern: for example, in criminal recidivism prediction, recidivism is only observed if the inmate is released; in lending applications, loan repayment is only observed if the loan is granted. We require that our algorithms satisfy common statistical fairness constraints (such as equalizing false positive or negative rates --- introduced as "equal opportunity" in Hardt et al. (2016)) at every round, with respect to the underlying distribution. We give upper and lower bounds characterizing the cost of this constraint in terms of the regret rate (and show that it is mild), and give an oracle efficient algorithm that achieves the upper bound.