Probabilistic Inference in Reinforcement Learning Done Right

A popular perspective in Reinforcement learning (RL) casts the problem as probabilistic inference on a graphical model of the Markov decision process (MDP). The core object of study is the probability of each state-action pair being visited under the optimal policy. Previous approaches to approximate this quantity can be arbitrarily poor, leading to algorithms that do not implement genuine statistical inference and consequently do not perform well in challenging problems. In this work, we undertake a rigorous Bayesian treatment of the posterior probability of state-action optimality and clarify how it flows through the MDP. We first reveal that this quantity can indeed be used to generate a policy that explores efficiently, as measured by regret. Unfortunately, computing it is intractable, so we derive a new variational Bayesian approximation yielding a tractable convex optimization problem and establish that the resulting policy also explores efficiently. We call our approach VAPOR and show that it has strong connections to Thompson sampling, K-learning, and maximum entropy exploration. We conclude with some experiments demonstrating the performance advantage of a deep RL version of VAPOR.

Efficient exploration via epistemic-risk-seeking policy optimization

Exploration remains a key challenge in deep reinforcement learning (RL). Optimism in the face of uncertainty is a well-known heuristic with theoretical guarantees in the tabular setting, but how best to translate the principle to deep reinforcement learning, which involves online stochastic gradients and deep network function approximators, is not fully understood. In this paper we propose a new, differentiable optimistic objective that when optimized yields a policy that provably explores efficiently, with guarantees even under function approximation. Our new objective is a zero-sum two-player game derived from endowing the agent with an epistemic-risk-seeking utility function, which converts uncertainty into value and encourages the agent to explore uncertain states. We show that the solution to this game minimizes an upper bound on the regret, with the `players' each attempting to minimize one component of a particular regret decomposition. We derive a new model-free algorithm which we call `epistemic-risk-seeking actor-critic', which is simply an application of simultaneous stochastic gradient ascent-descent to the game. We conclude with some results showing good performance of a deep RL agent using the technique on the challenging `DeepSea' environment, showing significant performance improvements even over other efficient exploration techniques, as well as results on the Atari benchmark.

ReLOAD: Reinforcement Learning with Optimistic Ascent-Descent for Last-Iterate Convergence in Constrained MDPs

In recent years, Reinforcement Learning (RL) has been applied to real-world problems with increasing success. Such applications often require to put constraints on the agent's behavior. Existing algorithms for constrained RL (CRL) rely on gradient descent-ascent, but this approach comes with a caveat. While these algorithms are guaranteed to converge on average, they do not guarantee last-iterate convergence, i.e., the current policy of the agent may never converge to the optimal solution. In practice, it is often observed that the policy alternates between satisfying the constraints and maximizing the reward, rarely accomplishing both objectives simultaneously. Here, we address this problem by introducing Reinforcement Learning with Optimistic Ascent-Descent (ReLOAD), a principled CRL method with guaranteed last-iterate convergence. We demonstrate its empirical effectiveness on a wide variety of CRL problems including discrete MDPs and continuous control. In the process we establish a benchmark of challenging CRL problems.

Optimistic Meta-Gradients

We study the connection between gradient-based meta-learning and convex op-timisation. We observe that gradient descent with momentum is a special case of meta-gradients, and building on recent results in optimisation, we prove convergence rates for meta-learning in the single task setting. While a meta-learned update rule can yield faster convergence up to constant factor, it is not sufficient for acceleration. Instead, some form of optimism is required. We show that optimism in meta-learning can be captured through Bootstrapped Meta-Gradients (Flennerhag et al., 2022), providing deeper insight into its underlying mechanics.

POMRL: No-Regret Learning-to-Plan with Increasing Horizons

We study the problem of planning under model uncertainty in an online meta-reinforcement learning (RL) setting where an agent is presented with a sequence of related tasks with limited interactions per task. The agent can use its experience in each task and across tasks to estimate both the transition model and the distribution over tasks. We propose an algorithm to meta-learn the underlying structure across tasks, utilize it to plan in each task, and upper-bound the regret of the planning loss. Our bound suggests that the average regret over tasks decreases as the number of tasks increases and as the tasks are more similar. In the classical single-task setting, it is known that the planning horizon should depend on the estimated model's accuracy, that is, on the number of samples within task. We generalize this finding to meta-RL and study this dependence of planning horizons on the number of tasks. Based on our theoretical findings, we derive heuristics for selecting slowly increasing discount factors, and we validate its significance empirically.

Variational Bayesian Optimistic Sampling

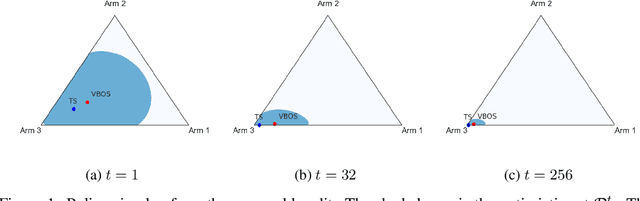
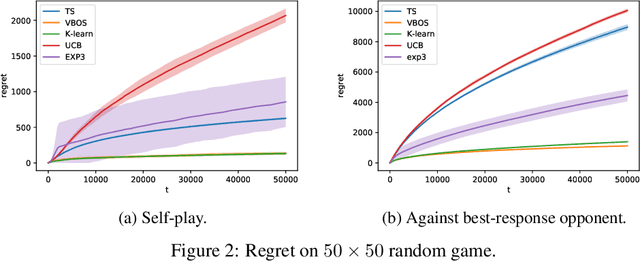
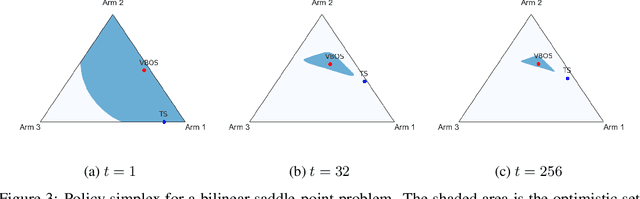
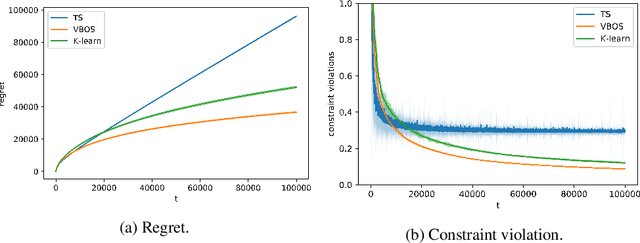
We consider online sequential decision problems where an agent must balance exploration and exploitation. We derive a set of Bayesian `optimistic' policies which, in the stochastic multi-armed bandit case, includes the Thompson sampling policy. We provide a new analysis showing that any algorithm producing policies in the optimistic set enjoys $\tilde O(\sqrt{AT})$ Bayesian regret for a problem with $A$ actions after $T$ rounds. We extend the regret analysis for optimistic policies to bilinear saddle-point problems which include zero-sum matrix games and constrained bandits as special cases. In this case we show that Thompson sampling can produce policies outside of the optimistic set and suffer linear regret in some instances. Finding a policy inside the optimistic set amounts to solving a convex optimization problem and we call the resulting algorithm `variational Bayesian optimistic sampling' (VBOS). The procedure works for any posteriors, \ie, it does not require the posterior to have any special properties, such as log-concavity, unimodality, or smoothness. The variational view of the problem has many useful properties, including the ability to tune the exploration-exploitation tradeoff, add regularization, incorporate constraints, and linearly parameterize the policy.

Evaluating Predictive Distributions: Does Bayesian Deep Learning Work?

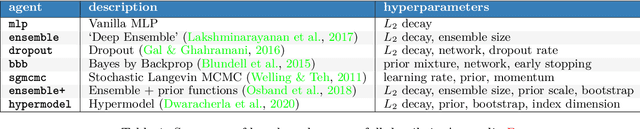
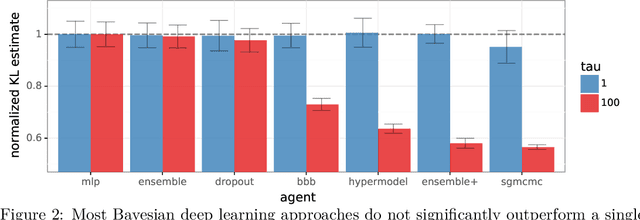
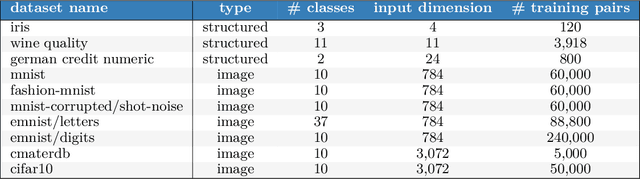
Posterior predictive distributions quantify uncertainties ignored by point estimates. This paper introduces \textit{The Neural Testbed}, which provides tools for the systematic evaluation of agents that generate such predictions. Crucially, these tools assess not only the quality of marginal predictions per input, but also joint predictions given many inputs. Joint distributions are often critical for useful uncertainty quantification, but they have been largely overlooked by the Bayesian deep learning community. We benchmark several approaches to uncertainty estimation using a neural-network-based data generating process. Our results reveal the importance of evaluation beyond marginal predictions. Further, they reconcile sources of confusion in the field, such as why Bayesian deep learning approaches that generate accurate marginal predictions perform poorly in sequential decision tasks, how incorporating priors can be helpful, and what roles epistemic versus aleatoric uncertainty play when evaluating performance. We also present experiments on real-world challenge datasets, which show a high correlation with testbed results, and that the importance of evaluating joint predictive distributions carries over to real data. As part of this effort, we opensource The Neural Testbed, including all implementations from this paper.

Discovering Diverse Nearly Optimal Policies withSuccessor Features

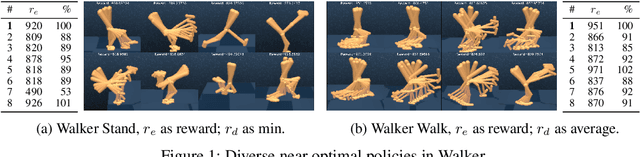
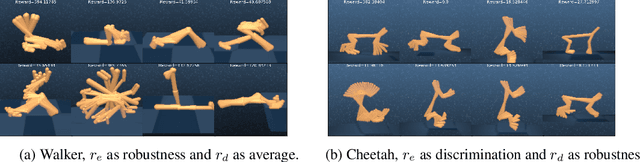
Finding different solutions to the same problem is a key aspect of intelligence associated with creativity and adaptation to novel situations. In reinforcement learning, a set of diverse policies can be useful for exploration, transfer, hierarchy, and robustness. We propose Diverse Successive Policies, a method for discovering policies that are diverse in the space of Successor Features, while assuring that they are near optimal. We formalize the problem as a Constrained Markov Decision Process (CMDP) where the goal is to find policies that maximize diversity, characterized by an intrinsic diversity reward, while remaining near-optimal with respect to the extrinsic reward of the MDP. We also analyze how recently proposed robustness and discrimination rewards perform and find that they are sensitive to the initialization of the procedure and may converge to sub-optimal solutions. To alleviate this, we propose new explicit diversity rewards that aim to minimize the correlation between the Successor Features of the policies in the set. We compare the different diversity mechanisms in the DeepMind Control Suite and find that the type of explicit diversity we are proposing is important to discover distinct behavior, like for example different locomotion patterns.

Reward is enough for convex MDPs

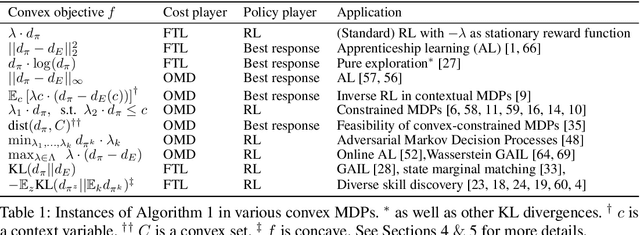
Maximising a cumulative reward function that is Markov and stationary, i.e., defined over state-action pairs and independent of time, is sufficient to capture many kinds of goals in a Markov Decision Process (MDP) based on the Reinforcement Learning (RL) problem formulation. However, not all goals can be captured in this manner. Specifically, it is easy to see that Convex MDPs in which goals are expressed as convex functions of stationary distributions cannot, in general, be formulated in this manner. In this paper, we reformulate the convex MDP problem as a min-max game between the policy and cost (negative reward) players using Fenchel duality and propose a meta-algorithm for solving it. We show that the average of the policies produced by an RL agent that maximizes the non-stationary reward produced by the cost player converges to an optimal solution to the convex MDP. Finally, we show that the meta-algorithm unifies several disparate branches of reinforcement learning algorithms in the literature, such as apprenticeship learning, variational intrinsic control, constrained MDPs, and pure exploration into a single framework.

Discovering a set of policies for the worst case reward

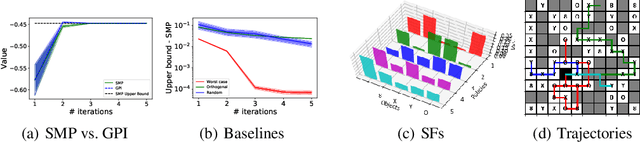
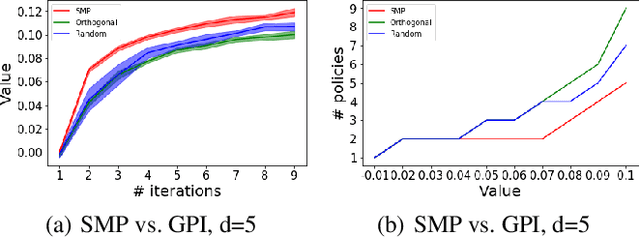
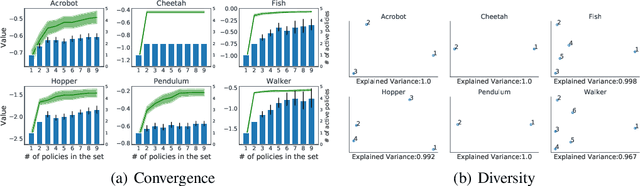
We study the problem of how to construct a set of policies that can be composed together to solve a collection of reinforcement learning tasks. Each task is a different reward function defined as a linear combination of known features. We consider a specific class of policy compositions which we call set improving policies (SIPs): given a set of policies and a set of tasks, a SIP is any composition of the former whose performance is at least as good as that of its constituents across all the tasks. We focus on the most conservative instantiation of SIPs, set-max policies (SMPs), so our analysis extends to any SIP. This includes known policy-composition operators like generalized policy improvement. Our main contribution is a policy iteration algorithm that builds a set of policies in order to maximize the worst-case performance of the resulting SMP on the set of tasks. The algorithm works by successively adding new policies to the set. We show that the worst-case performance of the resulting SMP strictly improves at each iteration, and the algorithm only stops when there does not exist a policy that leads to improved performance. We empirically evaluate our algorithm on a grid world and also on a set of domains from the DeepMind control suite. We confirm our theoretical results regarding the monotonically improving performance of our algorithm. Interestingly, we also show empirically that the sets of policies computed by the algorithm are diverse, leading to different trajectories in the grid world and very distinct locomotion skills in the control suite.