Approximate Thompson Sampling via Epistemic Neural Networks

Thompson sampling (TS) is a popular heuristic for action selection, but it requires sampling from a posterior distribution. Unfortunately, this can become computationally intractable in complex environments, such as those modeled using neural networks. Approximate posterior samples can produce effective actions, but only if they reasonably approximate joint predictive distributions of outputs across inputs. Notably, accuracy of marginal predictive distributions does not suffice. Epistemic neural networks (ENNs) are designed to produce accurate joint predictive distributions. We compare a range of ENNs through computational experiments that assess their performance in approximating TS across bandit and reinforcement learning environments. The results indicate that ENNs serve this purpose well and illustrate how the quality of joint predictive distributions drives performance. Further, we demonstrate that the \textit{epinet} -- a small additive network that estimates uncertainty -- matches the performance of large ensembles at orders of magnitude lower computational cost. This enables effective application of TS with computation that scales gracefully to complex environments.

Evaluating Predictive Distributions: Does Bayesian Deep Learning Work?

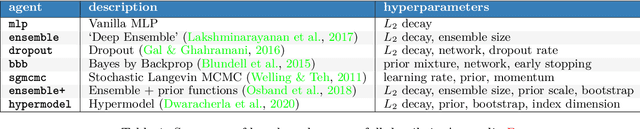
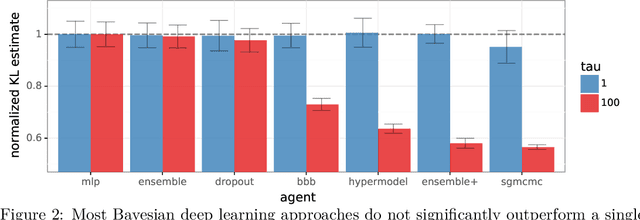
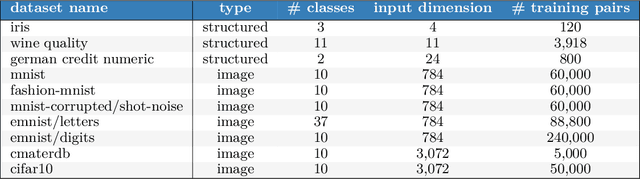
Posterior predictive distributions quantify uncertainties ignored by point estimates. This paper introduces \textit{The Neural Testbed}, which provides tools for the systematic evaluation of agents that generate such predictions. Crucially, these tools assess not only the quality of marginal predictions per input, but also joint predictions given many inputs. Joint distributions are often critical for useful uncertainty quantification, but they have been largely overlooked by the Bayesian deep learning community. We benchmark several approaches to uncertainty estimation using a neural-network-based data generating process. Our results reveal the importance of evaluation beyond marginal predictions. Further, they reconcile sources of confusion in the field, such as why Bayesian deep learning approaches that generate accurate marginal predictions perform poorly in sequential decision tasks, how incorporating priors can be helpful, and what roles epistemic versus aleatoric uncertainty play when evaluating performance. We also present experiments on real-world challenge datasets, which show a high correlation with testbed results, and that the importance of evaluating joint predictive distributions carries over to real data. As part of this effort, we opensource The Neural Testbed, including all implementations from this paper.

Epistemic Neural Networks

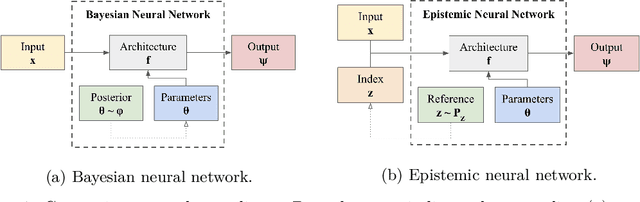
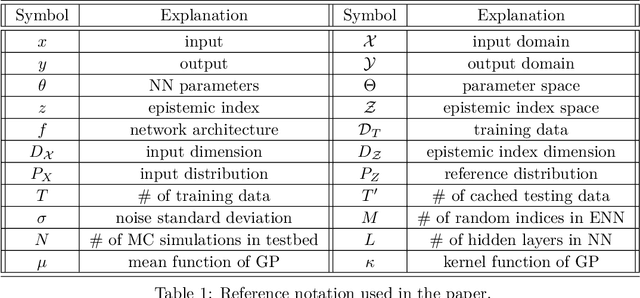
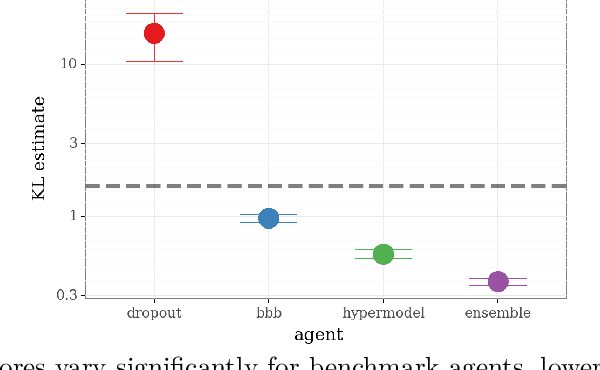
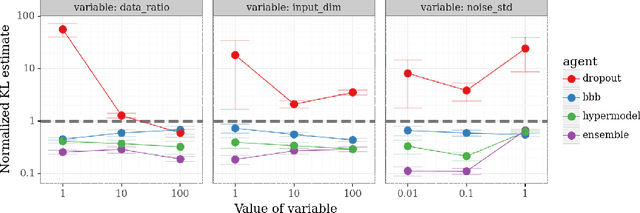
We introduce the \textit{epistemic neural network} (ENN) as an interface for uncertainty modeling in deep learning. All existing approaches to uncertainty modeling can be expressed as ENNs, and any ENN can be identified with a Bayesian neural network. However, this new perspective provides several promising directions for future research. Where prior work has developed probabilistic inference tools for neural networks; we ask instead, `which neural networks are suitable as tools for probabilistic inference?'. We propose a clear and simple metric for progress in ENNs: the KL-divergence with respect to a target distribution. We develop a computational testbed based on inference in a neural network Gaussian process and release our code as a benchmark at \url{https://github.com/deepmind/enn}. We evaluate several canonical approaches to uncertainty modeling in deep learning, and find they vary greatly in their performance. We provide insight to the sensitivity of these results and show that our metric is highly correlated with performance in sequential decision problems. Finally, we provide indications that new ENN architectures can improve performance in both the statistical quality and computational cost.

Reinforcement Learning, Bit by Bit

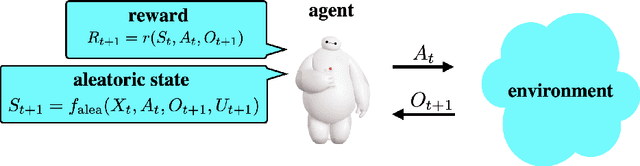
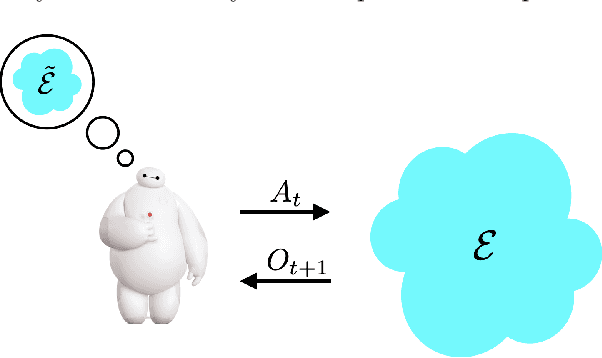
Reinforcement learning agents have demonstrated remarkable achievements in simulated environments. Data efficiency poses an impediment to carrying this success over to real environments. The design of data-efficient agents calls for a deeper understanding of information acquisition and representation. We develop concepts and establish a regret bound that together offer principled guidance. The bound sheds light on questions of what information to seek, how to seek that information, and it what information to retain. To illustrate concepts, we design simple agents that build on them and present computational results that demonstrate improvements in data efficiency.

Hypermodels for Exploration

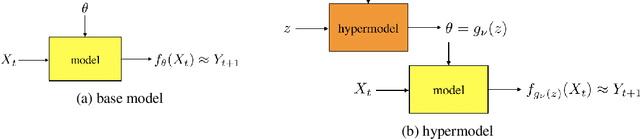
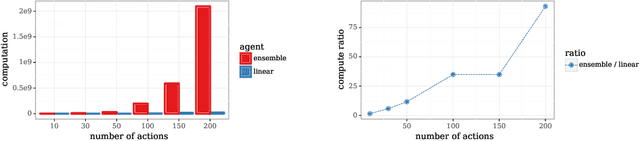
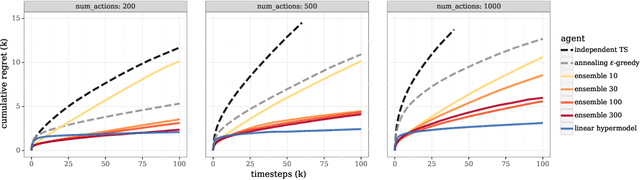
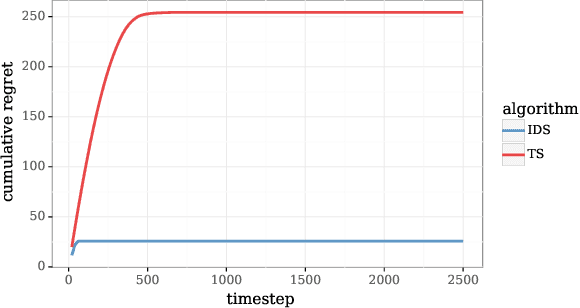
We study the use of hypermodels to represent epistemic uncertainty and guide exploration. This generalizes and extends the use of ensembles to approximate Thompson sampling. The computational cost of training an ensemble grows with its size, and as such, prior work has typically been limited to ensembles with tens of elements. We show that alternative hypermodels can enjoy dramatic efficiency gains, enabling behavior that would otherwise require hundreds or thousands of elements, and even succeed in situations where ensemble methods fail to learn regardless of size. This allows more accurate approximation of Thompson sampling as well as use of more sophisticated exploration schemes. In particular, we consider an approximate form of information-directed sampling and demonstrate performance gains relative to Thompson sampling. As alternatives to ensembles, we consider linear and neural network hypermodels, also known as hypernetworks. We prove that, with neural network base models, a linear hypermodel can represent essentially any distribution over functions, and as such, hypernetworks are no more expressive.

Support Recovery for the Drift Coefficient of High-Dimensional Diffusions

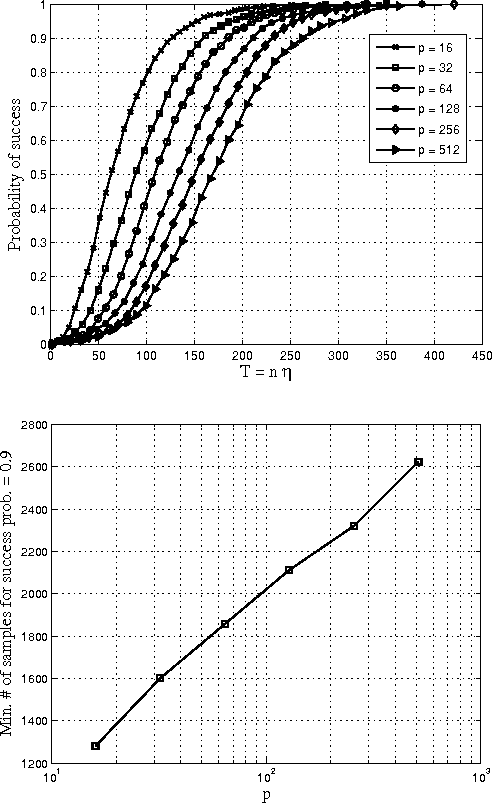
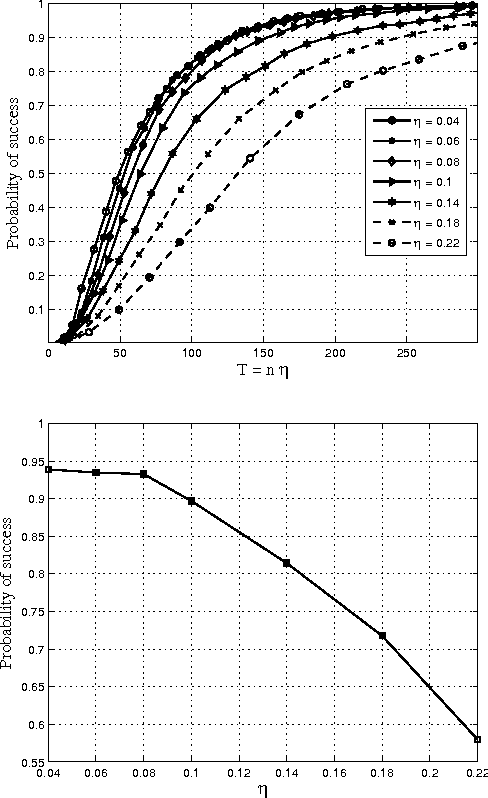
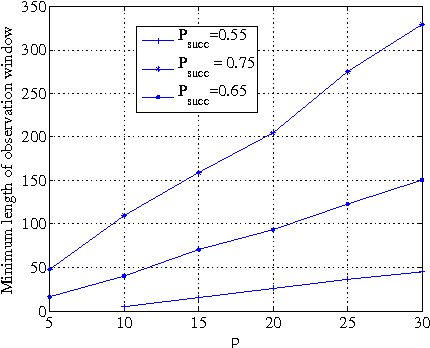
Consider the problem of learning the drift coefficient of a $p$-dimensional stochastic differential equation from a sample path of length $T$. We assume that the drift is parametrized by a high-dimensional vector, and study the support recovery problem when both $p$ and $T$ can tend to infinity. In particular, we prove a general lower bound on the sample-complexity $T$ by using a characterization of mutual information as a time integral of conditional variance, due to Kadota, Zakai, and Ziv. For linear stochastic differential equations, the drift coefficient is parametrized by a $p\times p$ matrix which describes which degrees of freedom interact under the dynamics. In this case, we analyze a $\ell_1$-regularized least squares estimator and prove an upper bound on $T$ that nearly matches the lower bound on specific classes of sparse matrices.

Accelerated Time-of-Flight Mass Spectrometry

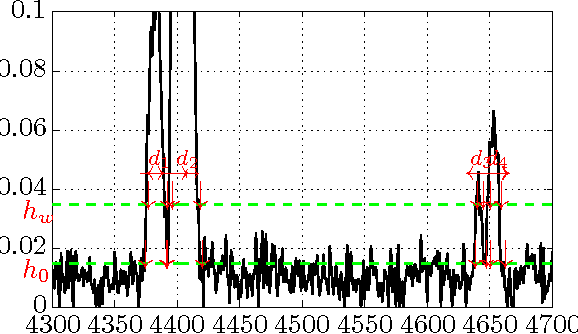
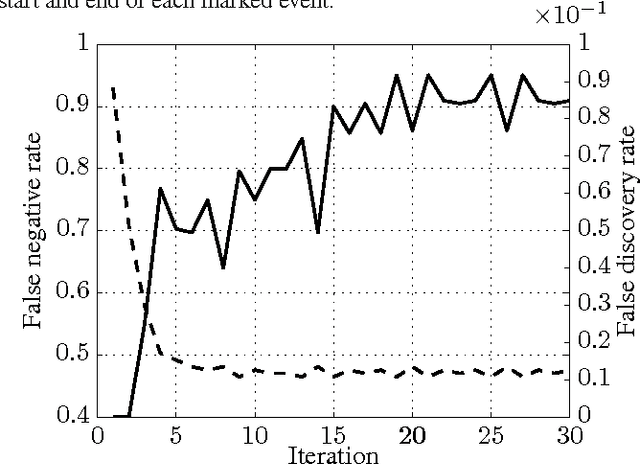
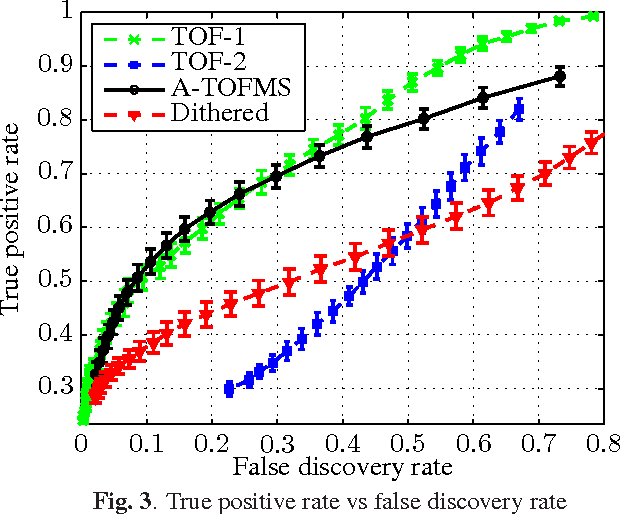
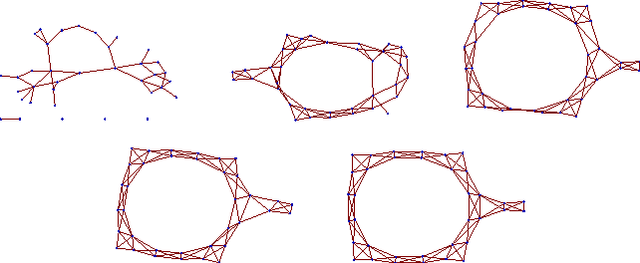
We study a simple modification to the conventional time of flight mass spectrometry (TOFMS) where a \emph{variable} and (pseudo)-\emph{random} pulsing rate is used which allows for traces from different pulses to overlap. This modification requires little alteration to the currently employed hardware. However, it requires a reconstruction method to recover the spectrum from highly aliased traces. We propose and demonstrate an efficient algorithm that can process massive TOFMS data using computational resources that can be considered modest with today's standards. This approach can be used to improve duty cycle, speed, and mass resolving power of TOFMS at the same time. We expect this to extend the applicability of TOFMS to new domains.

Efficient Reinforcement Learning for High Dimensional Linear Quadratic Systems

We study the problem of adaptive control of a high dimensional linear quadratic (LQ) system. Previous work established the asymptotic convergence to an optimal controller for various adaptive control schemes. More recently, for the average cost LQ problem, a regret bound of ${O}(\sqrt{T})$ was shown, apart form logarithmic factors. However, this bound scales exponentially with $p$, the dimension of the state space. In this work we consider the case where the matrices describing the dynamic of the LQ system are sparse and their dimensions are large. We present an adaptive control scheme that achieves a regret bound of ${O}(p \sqrt{T})$, apart from logarithmic factors. In particular, our algorithm has an average cost of $(1+\eps)$ times the optimum cost after $T = \polylog(p) O(1/\eps^2)$. This is in comparison to previous work on the dense dynamics where the algorithm requires time that scales exponentially with dimension in order to achieve regret of $\eps$ times the optimal cost. We believe that our result has prominent applications in the emerging area of computational advertising, in particular targeted online advertising and advertising in social networks.

Robust Max-Product Belief Propagation

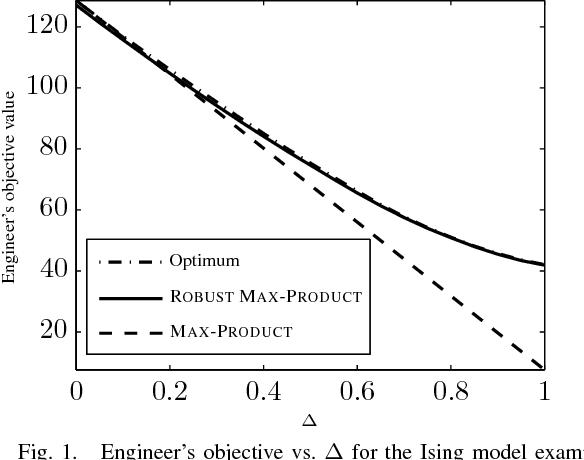
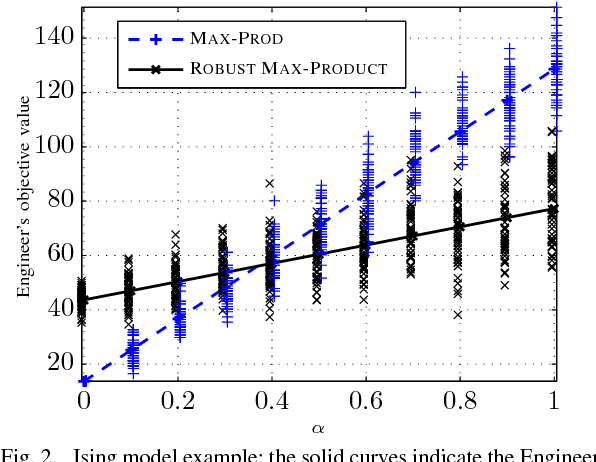
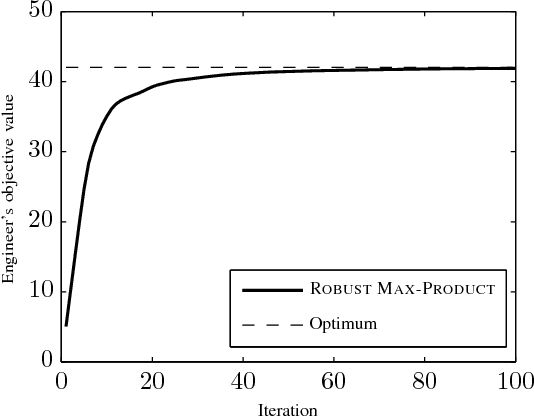
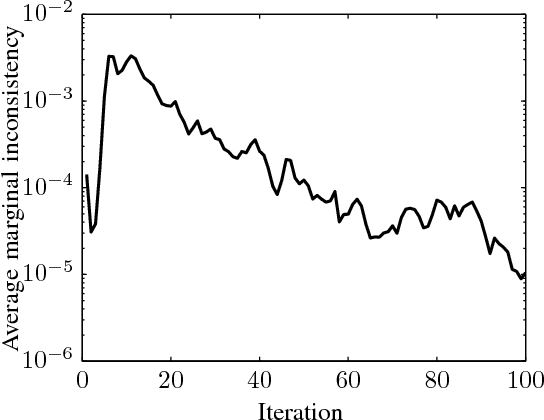
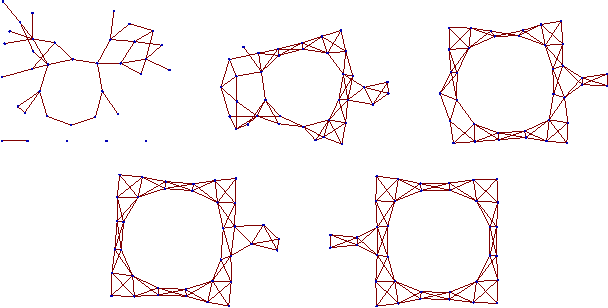
We study the problem of optimizing a graph-structured objective function under \emph{adversarial} uncertainty. This problem can be modeled as a two-persons zero-sum game between an Engineer and Nature. The Engineer controls a subset of the variables (nodes in the graph), and tries to assign their values to maximize an objective function. Nature controls the complementary subset of variables and tries to minimize the same objective. This setting encompasses estimation and optimization problems under model uncertainty, and strategic problems with a graph structure. Von Neumann's minimax theorem guarantees the existence of a (minimax) pair of randomized strategies that provide optimal robustness for each player against its adversary. We prove several structural properties of this strategy pair in the case of graph-structured payoff function. In particular, the randomized minimax strategies (distributions over variable assignments) can be chosen in such a way to satisfy the Markov property with respect to the graph. This significantly reduces the problem dimensionality. Finally we introduce a message passing algorithm to solve this minimax problem. The algorithm generalizes max-product belief propagation to this new domain.

Information Theoretic Limits on Learning Stochastic Differential Equations

Consider the problem of learning the drift coefficient of a stochastic differential equation from a sample path. In this paper, we assume that the drift is parametrized by a high dimensional vector. We address the question of how long the system needs to be observed in order to learn this vector of parameters. We prove a general lower bound on this time complexity by using a characterization of mutual information as time integral of conditional variance, due to Kadota, Zakai, and Ziv. This general lower bound is applied to specific classes of linear and non-linear stochastic differential equations. In the linear case, the problem under consideration is the one of learning a matrix of interaction coefficients. We evaluate our lower bound for ensembles of sparse and dense random matrices. The resulting estimates match the qualitative behavior of upper bounds achieved by computationally efficient procedures.