Matrix Factorization for Inferring Associations and Missing Links

Missing link prediction is a method for network analysis, with applications in recommender systems, biology, social sciences, cybersecurity, information retrieval, and Artificial Intelligence (AI) reasoning in Knowledge Graphs. Missing link prediction identifies unseen but potentially existing connections in a network by analyzing the observed patterns and relationships. In proliferation detection, this supports efforts to identify and characterize attempts by state and non-state actors to acquire nuclear weapons or associated technology - a notoriously challenging but vital mission for global security. Dimensionality reduction techniques like Non-Negative Matrix Factorization (NMF) and Logistic Matrix Factorization (LMF) are effective but require selection of the matrix rank parameter, that is, of the number of hidden features, k, to avoid over/under-fitting. We introduce novel Weighted (WNMFk), Boolean (BNMFk), and Recommender (RNMFk) matrix factorization methods, along with ensemble variants incorporating logistic factorization, for link prediction. Our methods integrate automatic model determination for rank estimation by evaluating stability and accuracy using a modified bootstrap methodology and uncertainty quantification (UQ), assessing prediction reliability under random perturbations. We incorporate Otsu threshold selection and k-means clustering for Boolean matrix factorization, comparing them to coordinate descent-based Boolean thresholding. Our experiments highlight the impact of rank k selection, evaluate model performance under varying test-set sizes, and demonstrate the benefits of UQ for reliable predictions using abstention. We validate our methods on three synthetic datasets (Boolean and uniformly distributed) and benchmark them against LMF and symmetric LMF (symLMF) on five real-world protein-protein interaction networks, showcasing an improved prediction performance.

Topological Signatures of Adversaries in Multimodal Alignments

Multimodal Machine Learning systems, particularly those aligning text and image data like CLIP/BLIP models, have become increasingly prevalent, yet remain susceptible to adversarial attacks. While substantial research has addressed adversarial robustness in unimodal contexts, defense strategies for multimodal systems are underexplored. This work investigates the topological signatures that arise between image and text embeddings and shows how adversarial attacks disrupt their alignment, introducing distinctive signatures. We specifically leverage persistent homology and introduce two novel Topological-Contrastive losses based on Total Persistence and Multi-scale kernel methods to analyze the topological signatures introduced by adversarial perturbations. We observe a pattern of monotonic changes in the proposed topological losses emerging in a wide range of attacks on image-text alignments, as more adversarial samples are introduced in the data. By designing an algorithm to back-propagate these signatures to input samples, we are able to integrate these signatures into Maximum Mean Discrepancy tests, creating a novel class of tests that leverage topological signatures for better adversarial detection.

HEAL: Hierarchical Embedding Alignment Loss for Improved Retrieval and Representation Learning

Retrieval-Augmented Generation (RAG) enhances Large Language Models (LLMs) by integrating external document retrieval to provide domain-specific or up-to-date knowledge. The effectiveness of RAG depends on the relevance of retrieved documents, which is influenced by the semantic alignment of embeddings with the domain's specialized content. Although full fine-tuning can align language models to specific domains, it is computationally intensive and demands substantial data. This paper introduces Hierarchical Embedding Alignment Loss (HEAL), a novel method that leverages hierarchical fuzzy clustering with matrix factorization within contrastive learning to efficiently align LLM embeddings with domain-specific content. HEAL computes level/depth-wise contrastive losses and incorporates hierarchical penalties to align embeddings with the underlying relationships in label hierarchies. This approach enhances retrieval relevance and document classification, effectively reducing hallucinations in LLM outputs. In our experiments, we benchmark and evaluate HEAL across diverse domains, including Healthcare, Material Science, Cyber-security, and Applied Maths.

LoRID: Low-Rank Iterative Diffusion for Adversarial Purification

This work presents an information-theoretic examination of diffusion-based purification methods, the state-of-the-art adversarial defenses that utilize diffusion models to remove malicious perturbations in adversarial examples. By theoretically characterizing the inherent purification errors associated with the Markov-based diffusion purifications, we introduce LoRID, a novel Low-Rank Iterative Diffusion purification method designed to remove adversarial perturbation with low intrinsic purification errors. LoRID centers around a multi-stage purification process that leverages multiple rounds of diffusion-denoising loops at the early time-steps of the diffusion models, and the integration of Tucker decomposition, an extension of matrix factorization, to remove adversarial noise at high-noise regimes. Consequently, LoRID increases the effective diffusion time-steps and overcomes strong adversarial attacks, achieving superior robustness performance in CIFAR-10/100, CelebA-HQ, and ImageNet datasets under both white-box and black-box settings.

LaFA: Latent Feature Attacks on Non-negative Matrix Factorization

As Machine Learning (ML) applications rapidly grow, concerns about adversarial attacks compromising their reliability have gained significant attention. One unsupervised ML method known for its resilience to such attacks is Non-negative Matrix Factorization (NMF), an algorithm that decomposes input data into lower-dimensional latent features. However, the introduction of powerful computational tools such as Pytorch enables the computation of gradients of the latent features with respect to the original data, raising concerns about NMF's reliability. Interestingly, naively deriving the adversarial loss for NMF as in the case of ML would result in the reconstruction loss, which can be shown theoretically to be an ineffective attacking objective. In this work, we introduce a novel class of attacks in NMF termed Latent Feature Attacks (LaFA), which aim to manipulate the latent features produced by the NMF process. Our method utilizes the Feature Error (FE) loss directly on the latent features. By employing FE loss, we generate perturbations in the original data that significantly affect the extracted latent features, revealing vulnerabilities akin to those found in other ML techniques. To handle large peak-memory overhead from gradient back-propagation in FE attacks, we develop a method based on implicit differentiation which enables their scaling to larger datasets. We validate NMF vulnerabilities and FE attacks effectiveness through extensive experiments on synthetic and real-world data.

Tensor Train Low-rank Approximation (TT-LoRA): Democratizing AI with Accelerated LLMs

In recent years, Large Language Models (LLMs) have demonstrated remarkable capabilities across a wide range of natural language processing (NLP) tasks, such as question-answering, sentiment analysis, text summarization, and machine translation. However, the ever-growing complexity of LLMs demands immense computational resources, hindering the broader research and application of these models. To address this, various parameter-efficient fine-tuning strategies, such as Low-Rank Approximation (LoRA) and Adapters, have been developed. Despite their potential, these methods often face limitations in compressibility. Specifically, LoRA struggles to scale effectively with the increasing number of trainable parameters in modern large scale LLMs. Additionally, Low-Rank Economic Tensor-Train Adaptation (LoRETTA), which utilizes tensor train decomposition, has not yet achieved the level of compression necessary for fine-tuning very large scale models with limited resources. This paper introduces Tensor Train Low-Rank Approximation (TT-LoRA), a novel parameter-efficient fine-tuning (PEFT) approach that extends LoRETTA with optimized tensor train (TT) decomposition integration. By eliminating Adapters and traditional LoRA-based structures, TT-LoRA achieves greater model compression without compromising downstream task performance, along with reduced inference latency and computational overhead. We conduct an exhaustive parameter search to establish benchmarks that highlight the trade-off between model compression and performance. Our results demonstrate significant compression of LLMs while maintaining comparable performance to larger models, facilitating their deployment on resource-constraint platforms.

Enhancing Code Translation in Language Models with Few-Shot Learning via Retrieval-Augmented Generation

The advent of large language models (LLMs) has significantly advanced the field of code translation, enabling automated translation between programming languages. However, these models often struggle with complex translation tasks due to inadequate contextual understanding. This paper introduces a novel approach that enhances code translation through Few-Shot Learning, augmented with retrieval-based techniques. By leveraging a repository of existing code translations, we dynamically retrieve the most relevant examples to guide the model in translating new code segments. Our method, based on Retrieval-Augmented Generation (RAG), substantially improves translation quality by providing contextual examples from which the model can learn in real-time. We selected RAG over traditional fine-tuning methods due to its ability to utilize existing codebases or a locally stored corpus of code, which allows for dynamic adaptation to diverse translation tasks without extensive retraining. Extensive experiments on diverse datasets with open LLM models such as Starcoder, Llama3-70B Instruct, CodeLlama-34B Instruct, Granite-34B Code Instruct, and Mixtral-8x22B, as well as commercial LLM models like GPT-3.5 Turbo and GPT-4o, demonstrate our approach's superiority over traditional zero-shot methods, especially in translating between Fortran and CPP. We also explored varying numbers of shots i.e. examples provided during inference, specifically 1, 2, and 3 shots and different embedding models for RAG, including Nomic-Embed, Starencoder, and CodeBERT, to assess the robustness and effectiveness of our approach.

Electrical Grid Anomaly Detection via Tensor Decomposition

Supervisory Control and Data Acquisition (SCADA) systems often serve as the nervous system for substations within power grids. These systems facilitate real-time monitoring, data acquisition, control of equipment, and ensure smooth and efficient operation of the substation and its connected devices. Previous work has shown that dimensionality reduction-based approaches, such as Principal Component Analysis (PCA), can be used for accurate identification of anomalies in SCADA systems. While not specifically applied to SCADA, non-negative matrix factorization (NMF) has shown strong results at detecting anomalies in wireless sensor networks. These unsupervised approaches model the normal or expected behavior and detect the unseen types of attacks or anomalies by identifying the events that deviate from the expected behavior. These approaches; however, do not model the complex and multi-dimensional interactions that are naturally present in SCADA systems. Differently, non-negative tensor decomposition is a powerful unsupervised machine learning (ML) method that can model the complex and multi-faceted activity details of SCADA events. In this work, we novelly apply the tensor decomposition method Canonical Polyadic Alternating Poisson Regression (CP-APR) with a probabilistic framework, which has previously shown state-of-the-art anomaly detection results on cyber network data, to identify anomalies in SCADA systems. We showcase that the use of statistical behavior analysis of SCADA communication with tensor decomposition improves the specificity and accuracy of identifying anomalies in electrical grid systems. In our experiments, we model real-world SCADA system data collected from the electrical grid operated by Los Alamos National Laboratory (LANL) which provides transmission and distribution service through a partnership with Los Alamos County, and detect synthetically generated anomalies.

Robust Adversarial Defense by Tensor Factorization

As machine learning techniques become increasingly prevalent in data analysis, the threat of adversarial attacks has surged, necessitating robust defense mechanisms. Among these defenses, methods exploiting low-rank approximations for input data preprocessing and neural network (NN) parameter factorization have shown potential. Our work advances this field further by integrating the tensorization of input data with low-rank decomposition and tensorization of NN parameters to enhance adversarial defense. The proposed approach demonstrates significant defense capabilities, maintaining robust accuracy even when subjected to the strongest known auto-attacks. Evaluations against leading-edge robust performance benchmarks reveal that our results not only hold their ground against the best defensive methods available but also exceed all current defense strategies that rely on tensor factorizations. This study underscores the potential of integrating tensorization and low-rank decomposition as a robust defense against adversarial attacks in machine learning.

Process Modeling, Hidden Markov Models, and Non-negative Tensor Factorization with Model Selection

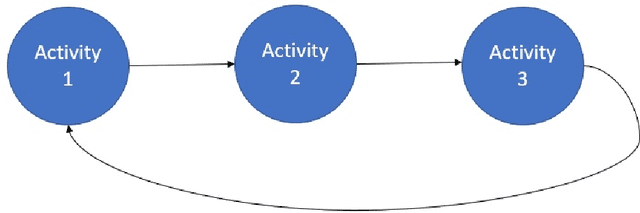
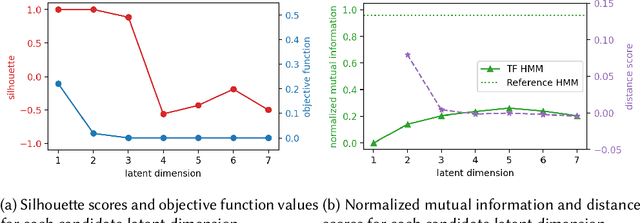
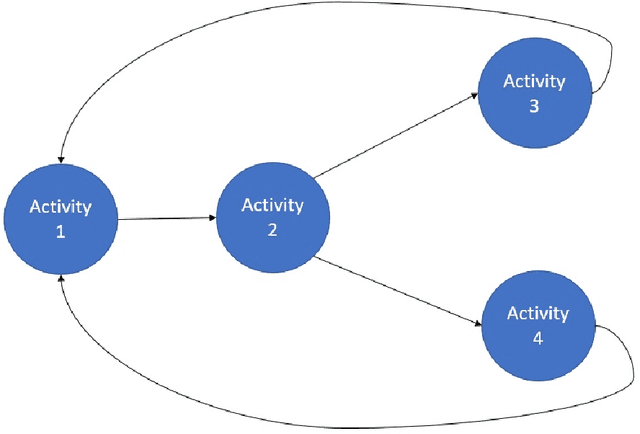
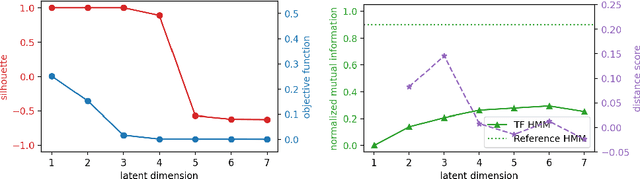
Monitoring of industrial processes is a critical capability in industry and in government to ensure reliability of production cycles, quick emergency response, and national security. Process monitoring allows users to gauge the involvement of an organization in an industrial process or predict the degradation or aging of machine parts in processes taking place at a remote location. Similar to many data science applications, we usually only have access to limited raw data, such as satellite imagery, short video clips, some event logs, and signatures captured by a small set of sensors. To combat data scarcity, we leverage the knowledge of subject matter experts (SMEs) who are familiar with the process. Various process mining techniques have been developed for this type of analysis; typically such approaches combine theoretical process models built based on domain expert insights with ad-hoc integration of available pieces of raw data. Here, we introduce a novel mathematically sound method that integrates theoretical process models (as proposed by SMEs) with interrelated minimal Hidden Markov Models (HMM), built via non-negative tensor factorization and discrete model simulations. Our method consolidates: (a) Theoretical process models development, (b) Discrete model simulations (c) HMM, (d) Joint Non-negative Matrix Factorization (NMF) and Non-negative Tensor Factorization (NTF), and (e) Custom model selection. To demonstrate our methodology and its abilities, we apply it on simple synthetic and real world process models.