Toric Geometry of Entropic Regularization

Entropic regularization is a method for large-scale linear programming. Geometrically, one traces intersections of the feasible polytope with scaled toric varieties, starting at the Birch point. We compare this to log-barrier methods, with reciprocal linear spaces, starting at the analytic center. We revisit entropic regularization for unbalanced optimal transport, and we develop the use of optimal conic couplings. We compute the degree of the associated toric variety, and we explore algorithms like iterative scaling.

Learning Paths from Signature Tensors

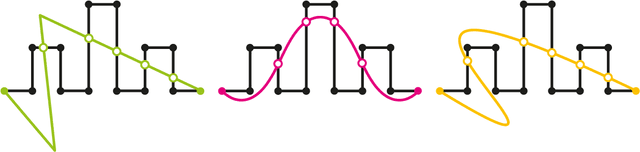
Matrix congruence extends naturally to the setting of tensors. We apply methods from tensor decomposition, algebraic geometry and numerical optimization to this group action. Given a tensor in the orbit of another tensor, we compute a matrix which transforms one to the other. Our primary application is an inverse problem from stochastic analysis: the recovery of paths from their signature tensors of order three. We establish identifiability results and recovery algorithms for piecewise linear paths, polynomial paths, and generic dictionaries. A detailed analysis of the relevant condition numbers is presented. We also compute the shortest path with a given signature tensor.

Changing Views on Curves and Surfaces

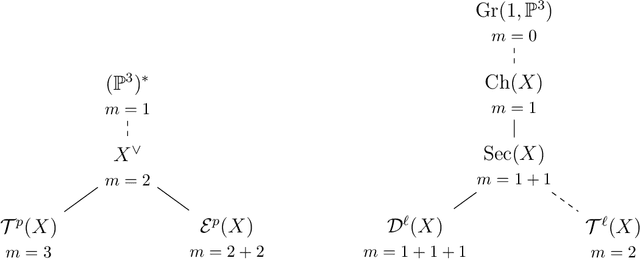
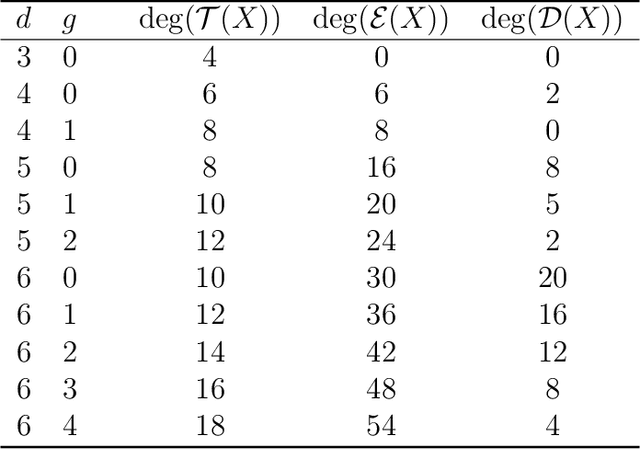
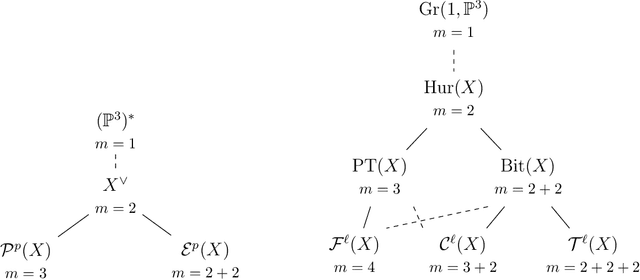
Visual events in computer vision are studied from the perspective of algebraic geometry. Given a sufficiently general curve or surface in 3-space, we consider the image or contour curve that arises by projecting from a viewpoint. Qualitative changes in that curve occur when the viewpoint crosses the visual event surface. We examine the components of this ruled surface, and observe that these coincide with the iterated singular loci of the coisotropic hypersurfaces associated with the original curve or surface. We derive formulas, due to Salmon and Petitjean, for the degrees of these surfaces, and show how to compute exact representations for all visual event surfaces using algebraic methods.

General models for rational cameras and the case of two-slit projections

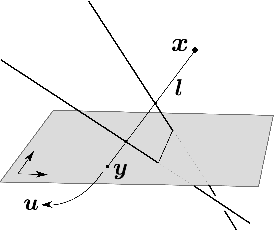
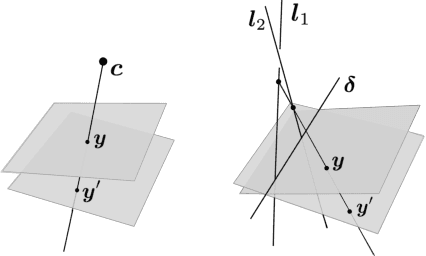
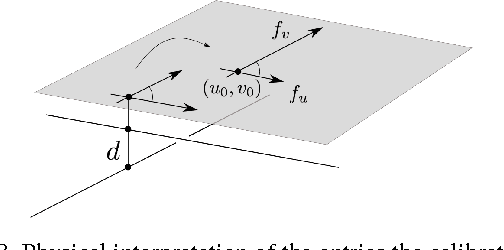
The rational camera model recently introduced in [19] provides a general methodology for studying abstract nonlinear imaging systems and their multi-view geometry. This paper builds on this framework to study "physical realizations" of rational cameras. More precisely, we give an explicit account of the mapping between between physical visual rays and image points (missing in the original description), which allows us to give simple analytical expressions for direct and inverse projections. We also consider "primitive" camera models, that are orbits under the action of various projective transformations, and lead to a general notion of intrinsic parameters. The methodology is general, but it is illustrated concretely by an in-depth study of two-slit cameras, that we model using pairs of linear projections. This simple analytical form allows us to describe models for the corresponding primitive cameras, to introduce intrinsic parameters with a clear geometric meaning, and to define an epipolar tensor characterizing two-view correspondences. In turn, this leads to new algorithms for structure from motion and self-calibration.

A clever elimination strategy for efficient minimal solvers

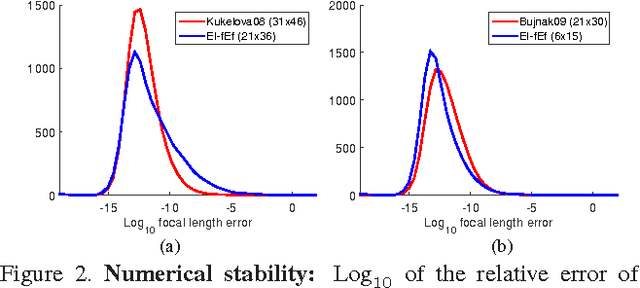
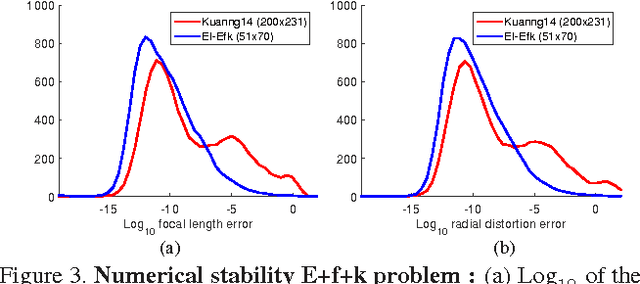
We present a new insight into the systematic generation of minimal solvers in computer vision, which leads to smaller and faster solvers. Many minimal problem formulations are coupled sets of linear and polynomial equations where image measurements enter the linear equations only. We show that it is useful to solve such systems by first eliminating all the unknowns that do not appear in the linear equations and then extending solutions to the rest of unknowns. This can be generalized to fully non-linear systems by linearization via lifting. We demonstrate that this approach leads to more efficient solvers in three problems of partially calibrated relative camera pose computation with unknown focal length and/or radial distortion. Our approach also generates new interesting constraints on the fundamental matrices of partially calibrated cameras, which were not known before.

Congruences and Concurrent Lines in Multi-View Geometry

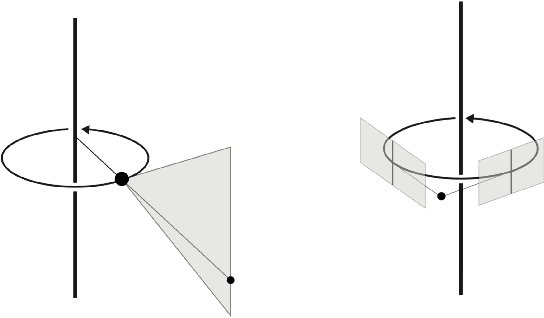
We present a new framework for multi-view geometry in computer vision. A camera is a mapping between $\mathbb{P}^3$ and a line congruence. This model, which ignores image planes and measurements, is a natural abstraction of traditional pinhole cameras. It includes two-slit cameras, pushbroom cameras, catadioptric cameras, and many more. We study the concurrent lines variety, which consists of $n$-tuples of lines in $\mathbb{P}^3$ that intersect at a point. Combining its equations with those of various congruences, we derive constraints for corresponding images in multiple views. We also study photographic cameras which use image measurements and are modeled as rational maps from $\mathbb{P}^3$ to $\mathbb{P}^2$ or $\mathbb{P}^1\times \mathbb{P}^1$.

Distortion Varieties

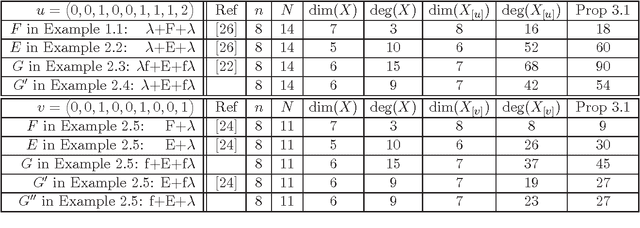
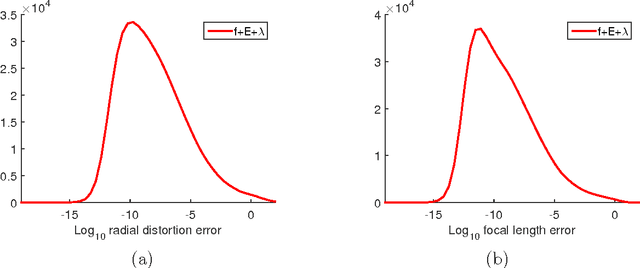
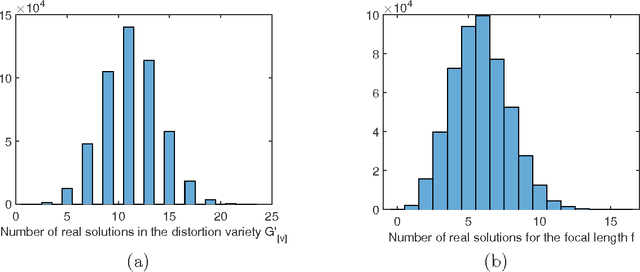
The distortion varieties of a given projective variety are parametrized by duplicating coordinates and multiplying them with monomials. We study their degrees and defining equations. Exact formulas are obtained for the case of one-parameter distortions. These are based on Chow polytopes and Gr\"obner bases. Multi-parameter distortions are studied using tropical geometry. The motivation for distortion varieties comes from multi-view geometry in computer vision. Our theory furnishes a new framework for formulating and solving minimal problems for camera models with image distortion.

Rigid Multiview Varieties

The multiview variety from computer vision is generalized to images by $n$ cameras of points linked by a distance constraint. The resulting five-dimensional variety lives in a product of $2n$ projective planes. We determine defining polynomial equations, and we explore generalizations of this variety to scenarios of interest in applications.

On the Existence of Epipolar Matrices

This paper considers the foundational question of the existence of a fundamental (resp. essential) matrix given $m$ point correspondences in two views. We present a complete answer for the existence of fundamental matrices for any value of $m$. Using examples we disprove the widely held beliefs that fundamental matrices always exist whenever $m \leq 7$. At the same time, we prove that they exist unconditionally when $m \leq 5$. Under a mild genericity condition, we show that an essential matrix always exists when $m \leq 4$. We also characterize the six and seven point configurations in two views for which all matrices satisfying the epipolar constraint have rank at most one.

Certifying the Existence of Epipolar Matrices

Given a set of point correspondences in two images, the existence of a fundamental matrix is a necessary condition for the points to be the images of a 3-dimensional scene imaged with two pinhole cameras. If the camera calibration is known then one requires the existence of an essential matrix. We present an efficient algorithm, using exact linear algebra, for testing the existence of a fundamental matrix. The input is any number of point correspondences. For essential matrices, we characterize the solvability of the Demazure polynomials. In both scenarios, we determine which linear subspaces intersect a fixed set defined by non-linear polynomials. The conditions we derive are polynomials stated purely in terms of image coordinates. They represent a new class of two-view invariants, free of fundamental (resp.~essential)~matrices.