Babak Shahbaba
Heterogeneous Graph Alignment for Joint Reasoning and Interpretability
Jan 30, 2026Abstract:Multi-graph learning is crucial for extracting meaningful signals from collections of heterogeneous graphs. However, effectively integrating information across graphs with differing topologies, scales, and semantics, often in the absence of shared node identities, remains a significant challenge. We present the Multi-Graph Meta-Transformer (MGMT), a unified, scalable, and interpretable framework for cross-graph learning. MGMT first applies Graph Transformer encoders to each graph, mapping structure and attributes into a shared latent space. It then selects task-relevant supernodes via attention and builds a meta-graph that connects functionally aligned supernodes across graphs using similarity in the latent space. Additional Graph Transformer layers on this meta-graph enable joint reasoning over intra- and inter-graph structure. The meta-graph provides built-in interpretability: supernodes and superedges highlight influential substructures and cross-graph alignments. Evaluating MGMT on both synthetic datasets and real-world neuroscience applications, we show that MGMT consistently outperforms existing state-of-the-art models in graph-level prediction tasks while offering interpretable representations that facilitate scientific discoveries. Our work establishes MGMT as a unified framework for structured multi-graph learning, advancing representation techniques in domains where graph-based data plays a central role.
Neural-Inspired Posterior Approximation (NIPA)
Jan 30, 2026Abstract:Humans learn efficiently from their environment by engaging multiple interacting neural systems that support distinct yet complementary forms of control, including model-based (goal-directed) planning, model-free (habitual) responding, and episodic memory-based learning. Model-based mechanisms compute prospective action values using an internal model of the environment, supporting flexible but computationally costly planning; model-free mechanisms cache value estimates and build heuristics that enable fast, efficient habitual responding; and memory-based mechanisms allow rapid adaptation from individual experience. In this work, we aim to elucidate the computational principles underlying this biological efficiency and translate them into a sampling algorithm for scalable Bayesian inference through effective exploration of the posterior distribution. More specifically, our proposed algorithm comprises three components: a model-based module that uses the target distribution for guided but computationally slow sampling; a model-free module that uses previous samples to learn patterns in the parameter space, enabling fast, reflexive sampling without directly evaluating the expensive target distribution; and an episodic-control module that supports rapid sampling by recalling specific past events (i.e., samples). We show that this approach advances Bayesian methods and facilitates their application to large-scale statistical machine learning problems. In particular, we apply our proposed framework to Bayesian deep learning, with an emphasis on proper and principled uncertainty quantification.
Meta Fusion: A Unified Framework For Multimodality Fusion with Mutual Learning
Jul 27, 2025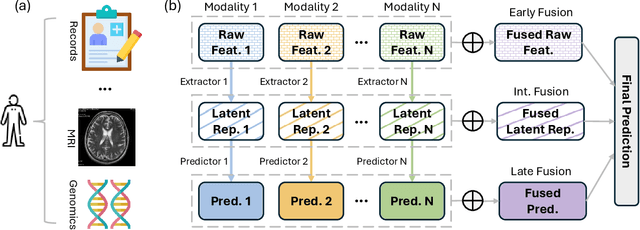
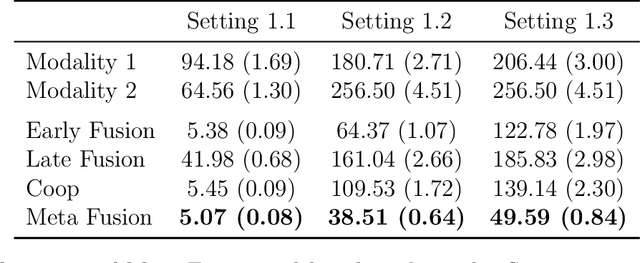
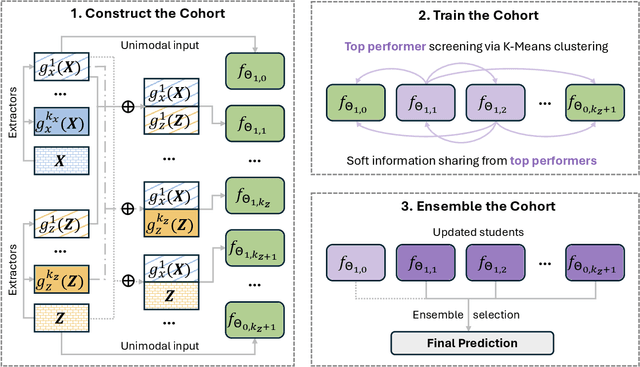
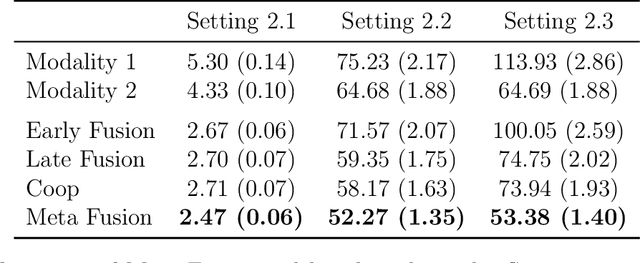
Abstract:Developing effective multimodal data fusion strategies has become increasingly essential for improving the predictive power of statistical machine learning methods across a wide range of applications, from autonomous driving to medical diagnosis. Traditional fusion methods, including early, intermediate, and late fusion, integrate data at different stages, each offering distinct advantages and limitations. In this paper, we introduce Meta Fusion, a flexible and principled framework that unifies these existing strategies as special cases. Motivated by deep mutual learning and ensemble learning, Meta Fusion constructs a cohort of models based on various combinations of latent representations across modalities, and further boosts predictive performance through soft information sharing within the cohort. Our approach is model-agnostic in learning the latent representations, allowing it to flexibly adapt to the unique characteristics of each modality. Theoretically, our soft information sharing mechanism reduces the generalization error. Empirically, Meta Fusion consistently outperforms conventional fusion strategies in extensive simulation studies. We further validate our approach on real-world applications, including Alzheimer's disease detection and neural decoding.
Reinforcement Learning for Individual Optimal Policy from Heterogeneous Data
May 14, 2025Abstract:Offline reinforcement learning (RL) aims to find optimal policies in dynamic environments in order to maximize the expected total rewards by leveraging pre-collected data. Learning from heterogeneous data is one of the fundamental challenges in offline RL. Traditional methods focus on learning an optimal policy for all individuals with pre-collected data from a single episode or homogeneous batch episodes, and thus, may result in a suboptimal policy for a heterogeneous population. In this paper, we propose an individualized offline policy optimization framework for heterogeneous time-stationary Markov decision processes (MDPs). The proposed heterogeneous model with individual latent variables enables us to efficiently estimate the individual Q-functions, and our Penalized Pessimistic Personalized Policy Learning (P4L) algorithm guarantees a fast rate on the average regret under a weak partial coverage assumption on behavior policies. In addition, our simulation studies and a real data application demonstrate the superior numerical performance of the proposed method compared with existing methods.
Weakly-Supervised Multimodal Learning on MIMIC-CXR
Nov 15, 2024



Abstract:Multimodal data integration and label scarcity pose significant challenges for machine learning in medical settings. To address these issues, we conduct an in-depth evaluation of the newly proposed Multimodal Variational Mixture-of-Experts (MMVM) VAE on the challenging MIMIC-CXR dataset. Our analysis demonstrates that the MMVM VAE consistently outperforms other multimodal VAEs and fully supervised approaches, highlighting its strong potential for real-world medical applications.
Optimal Transport for Latent Integration with An Application to Heterogeneous Neuronal Activity Data
Jun 27, 2024



Abstract:Detecting dynamic patterns of task-specific responses shared across heterogeneous datasets is an essential and challenging problem in many scientific applications in medical science and neuroscience. In our motivating example of rodent electrophysiological data, identifying the dynamical patterns in neuronal activity associated with ongoing cognitive demands and behavior is key to uncovering the neural mechanisms of memory. One of the greatest challenges in investigating a cross-subject biological process is that the systematic heterogeneity across individuals could significantly undermine the power of existing machine learning methods to identify the underlying biological dynamics. In addition, many technically challenging neurobiological experiments are conducted on only a handful of subjects where rich longitudinal data are available for each subject. The low sample sizes of such experiments could further reduce the power to detect common dynamic patterns among subjects. In this paper, we propose a novel heterogeneous data integration framework based on optimal transport to extract shared patterns in complex biological processes. The key advantages of the proposed method are that it can increase discriminating power in identifying common patterns by reducing heterogeneity unrelated to the signal by aligning the extracted latent spatiotemporal information across subjects. Our approach is effective even with a small number of subjects, and does not require auxiliary matching information for the alignment. In particular, our method can align longitudinal data across heterogeneous subjects in a common latent space to capture the dynamics of shared patterns while utilizing temporal dependency within subjects.
A Model-Agnostic Graph Neural Network for Integrating Local and Global Information
Oct 02, 2023Abstract:Graph Neural Networks (GNNs) have achieved promising performance in a variety of graph-focused tasks. Despite their success, existing GNNs suffer from two significant limitations: a lack of interpretability in results due to their black-box nature, and an inability to learn representations of varying orders. To tackle these issues, we propose a novel Model-agnostic Graph Neural Network (MaGNet) framework, which is able to sequentially integrate information of various orders, extract knowledge from high-order neighbors, and provide meaningful and interpretable results by identifying influential compact graph structures. In particular, MaGNet consists of two components: an estimation model for the latent representation of complex relationships under graph topology, and an interpretation model that identifies influential nodes, edges, and important node features. Theoretically, we establish the generalization error bound for MaGNet via empirical Rademacher complexity, and showcase its power to represent layer-wise neighborhood mixing. We conduct comprehensive numerical studies using simulated data to demonstrate the superior performance of MaGNet in comparison to several state-of-the-art alternatives. Furthermore, we apply MaGNet to a real-world case study aimed at extracting task-critical information from brain activity data, thereby highlighting its effectiveness in advancing scientific research.
Fully Bayesian Autoencoders with Latent Sparse Gaussian Processes
Feb 09, 2023



Abstract:Autoencoders and their variants are among the most widely used models in representation learning and generative modeling. However, autoencoder-based models usually assume that the learned representations are i.i.d. and fail to capture the correlations between the data samples. To address this issue, we propose a novel Sparse Gaussian Process Bayesian Autoencoder (SGPBAE) model in which we impose fully Bayesian sparse Gaussian Process priors on the latent space of a Bayesian Autoencoder. We perform posterior estimation for this model via stochastic gradient Hamiltonian Monte Carlo. We evaluate our approach qualitatively and quantitatively on a wide range of representation learning and generative modeling tasks and show that our approach consistently outperforms multiple alternatives relying on Variational Autoencoders.
Scaling Up Bayesian Uncertainty Quantification for Inverse Problems using Deep Neural Networks
Jan 11, 2021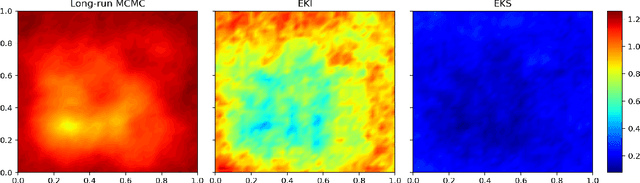
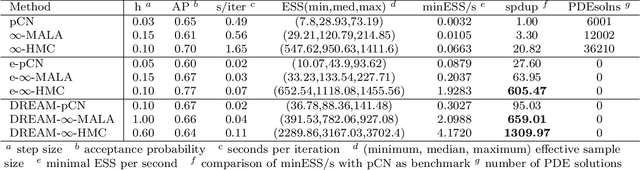
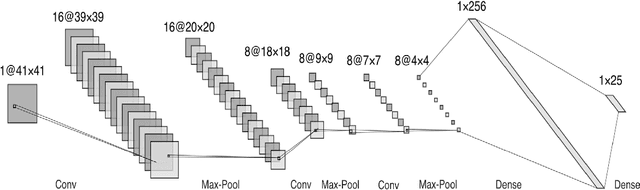
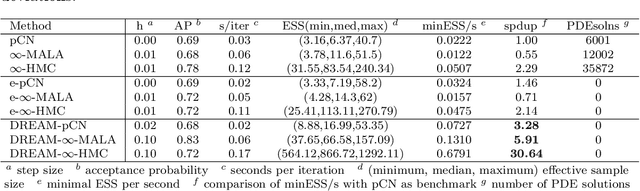
Abstract:Due to the importance of uncertainty quantification (UQ), Bayesian approach to inverse problems has recently gained popularity in applied mathematics, physics, and engineering. However, traditional Bayesian inference methods based on Markov Chain Monte Carlo (MCMC) tend to be computationally intensive and inefficient for such high dimensional problems. To address this issue, several methods based on surrogate models have been proposed to speed up the inference process. More specifically, the calibration-emulation-sampling (CES) scheme has been proven to be successful in large dimensional UQ problems. In this work, we propose a novel CES approach for Bayesian inference based on deep neural network (DNN) models for the emulation phase. The resulting algorithm is not only computationally more efficient, but also less sensitive to the training set. Further, by using an Autoencoder (AE) for dimension reduction, we have been able to speed up our Bayesian inference method up to three orders of magnitude. Overall, our method, henceforth called \emph{Dimension-Reduced Emulative Autoencoder Monte Carlo (DREAM)} algorithm, is able to scale Bayesian UQ up to thousands of dimensions in physics-constrained inverse problems. Using two low-dimensional (linear and nonlinear) inverse problems we illustrate the validity this approach. Next, we apply our method to two high-dimensional numerical examples (elliptic and advection-diffussion) to demonstrate its computational advantage over existing algorithms.
Conjoined Dirichlet Process
Feb 08, 2020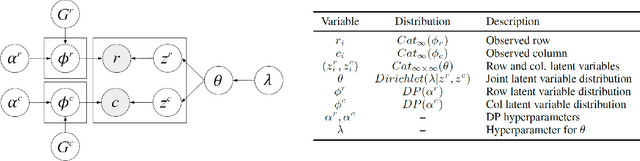

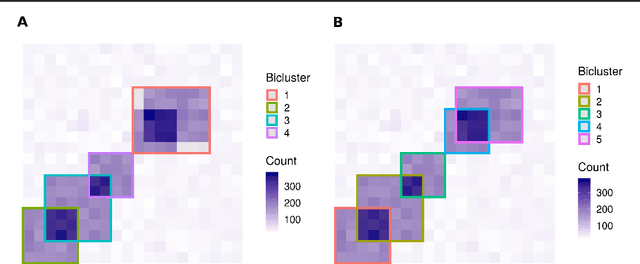

Abstract:Biclustering is a class of techniques that simultaneously clusters the rows and columns of a matrix to sort heterogeneous data into homogeneous blocks. Although many algorithms have been proposed to find biclusters, existing methods suffer from the pre-specification of the number of biclusters or place constraints on the model structure. To address these issues, we develop a novel, non-parametric probabilistic biclustering method based on Dirichlet processes to identify biclusters with strong co-occurrence in both rows and columns. The proposed method utilizes dual Dirichlet process mixture models to learn row and column clusters, with the number of resulting clusters determined by the data rather than pre-specified. Probabilistic biclusters are identified by modeling the mutual dependence between the row and column clusters. We apply our method to two different applications, text mining and gene expression analysis, and demonstrate that our method improves bicluster extraction in many settings compared to existing approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge