TDD-Bench Verified: Can LLMs Generate Tests for Issues Before They Get Resolved?

Test-driven development (TDD) is the practice of writing tests first and coding later, and the proponents of TDD expound its numerous benefits. For instance, given an issue on a source code repository, tests can clarify the desired behavior among stake-holders before anyone writes code for the agreed-upon fix. Although there has been a lot of work on automated test generation for the practice "write code first, test later", there has been little such automation for TDD. Ideally, tests for TDD should be fail-to-pass (i.e., fail before the issue is resolved and pass after) and have good adequacy with respect to covering the code changed during issue resolution. This paper introduces TDD-Bench Verified, a high-quality benchmark suite of 449 issues mined from real-world GitHub code repositories. The benchmark's evaluation harness runs only relevant tests in isolation for simple yet accurate coverage measurements, and the benchmark's dataset is filtered both by human judges and by execution in the harness. This paper also presents Auto-TDD, an LLM-based solution that takes as input an issue description and a codebase (prior to issue resolution) and returns as output a test that can be used to validate the changes made for resolving the issue. Our evaluation shows that Auto-TDD yields a better fail-to-pass rate than the strongest prior work while also yielding high coverage adequacy. Overall, we hope that this work helps make developers more productive at resolving issues while simultaneously leading to more robust fixes.

Navigating Ensemble Configurations for Algorithmic Fairness

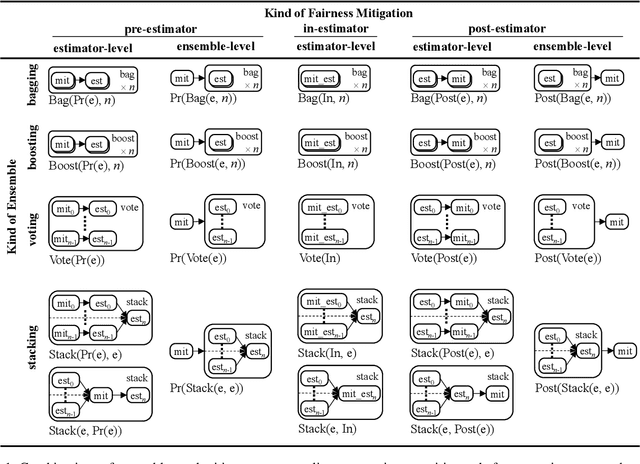
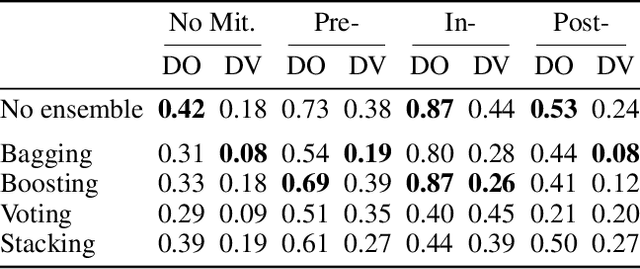
Bias mitigators can improve algorithmic fairness in machine learning models, but their effect on fairness is often not stable across data splits. A popular approach to train more stable models is ensemble learning, but unfortunately, it is unclear how to combine ensembles with mitigators to best navigate trade-offs between fairness and predictive performance. To that end, we built an open-source library enabling the modular composition of 8 mitigators, 4 ensembles, and their corresponding hyperparameters, and we empirically explored the space of configurations on 13 datasets. We distilled our insights from this exploration in the form of a guidance diagram for practitioners that we demonstrate is robust and reproducible.

Formalization of a Stochastic Approximation Theorem

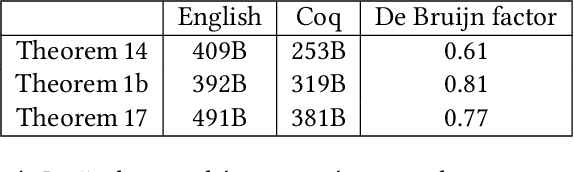
Stochastic approximation algorithms are iterative procedures which are used to approximate a target value in an environment where the target is unknown and direct observations are corrupted by noise. These algorithms are useful, for instance, for root-finding and function minimization when the target function or model is not directly known. Originally introduced in a 1951 paper by Robbins and Monro, the field of Stochastic approximation has grown enormously and has come to influence application domains from adaptive signal processing to artificial intelligence. As an example, the Stochastic Gradient Descent algorithm which is ubiquitous in various subdomains of Machine Learning is based on stochastic approximation theory. In this paper, we give a formal proof (in the Coq proof assistant) of a general convergence theorem due to Aryeh Dvoretzky, which implies the convergence of important classical methods such as the Robbins-Monro and the Kiefer-Wolfowitz algorithms. In the process, we build a comprehensive Coq library of measure-theoretic probability theory and stochastic processes.

An Empirical Study of Modular Bias Mitigators and Ensembles

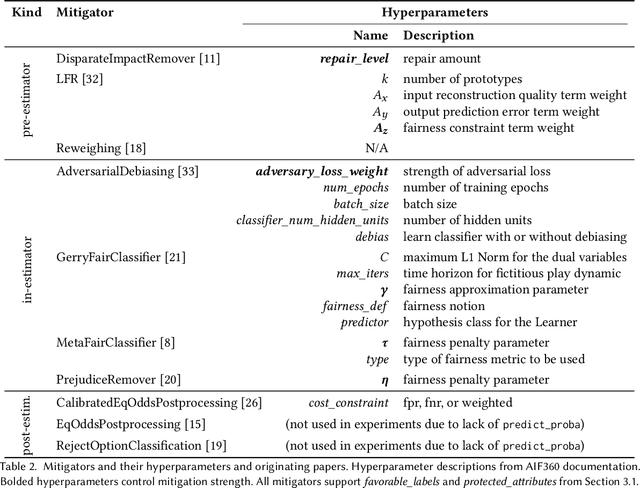
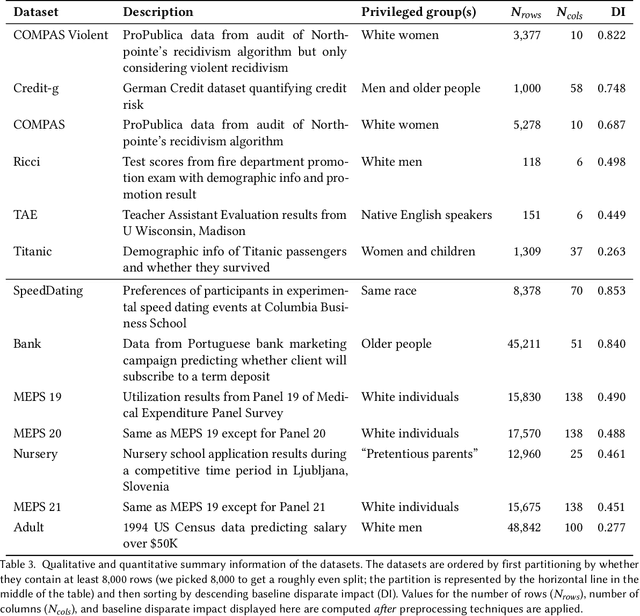
There are several bias mitigators that can reduce algorithmic bias in machine learning models but, unfortunately, the effect of mitigators on fairness is often not stable when measured across different data splits. A popular approach to train more stable models is ensemble learning. Ensembles, such as bagging, boosting, voting, or stacking, have been successful at making predictive performance more stable. One might therefore ask whether we can combine the advantages of bias mitigators and ensembles? To explore this question, we first need bias mitigators and ensembles to work together. We built an open-source library enabling the modular composition of 10 mitigators, 4 ensembles, and their corresponding hyperparameters. Based on this library, we empirically explored the space of combinations on 13 datasets, including datasets commonly used in fairness literature plus datasets newly curated by our library. Furthermore, we distilled the results into a guidance diagram for practitioners. We hope this paper will contribute towards improving stability in bias mitigation.

CertRL: Formalizing Convergence Proofs for Value and Policy Iteration in Coq

Reinforcement learning algorithms solve sequential decision-making problems in probabilistic environments by optimizing for long-term reward. The desire to use reinforcement learning in safety-critical settings inspires a recent line of work on formally constrained reinforcement learning; however, these methods place the implementation of the learning algorithm in their Trusted Computing Base. The crucial correctness property of these implementations is a guarantee that the learning algorithm converges to an optimal policy. This paper begins the work of closing this gap by developing a Coq formalization of two canonical reinforcement learning algorithms: value and policy iteration for finite state Markov decision processes. The central results are a formalization of Bellman's optimality principle and its proof, which uses a contraction property of Bellman optimality operator to establish that a sequence converges in the infinite horizon limit. The CertRL development exemplifies how the Giry monad and mechanized metric coinduction streamline optimality proofs for reinforcement learning algorithms. The CertRL library provides a general framework for proving properties about Markov decision processes and reinforcement learning algorithms, paving the way for further work on formalization of reinforcement learning algorithms.

Lale: Consistent Automated Machine Learning

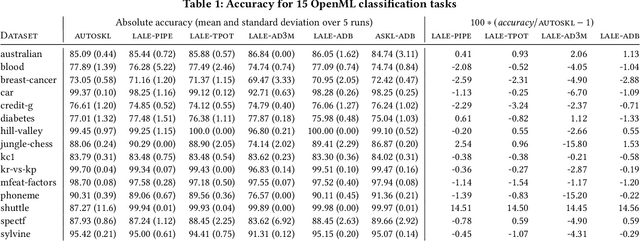
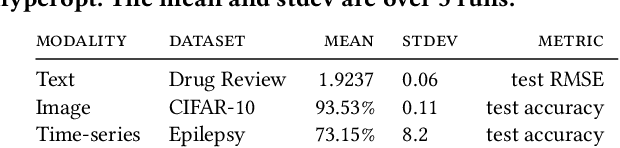
Automated machine learning makes it easier for data scientists to develop pipelines by searching over possible choices for hyperparameters, algorithms, and even pipeline topologies. Unfortunately, the syntax for automated machine learning tools is inconsistent with manual machine learning, with each other, and with error checks. Furthermore, few tools support advanced features such as topology search or higher-order operators. This paper introduces Lale, a library of high-level Python interfaces that simplifies and unifies automated machine learning in a consistent way.

Type-Driven Automated Learning with Lale

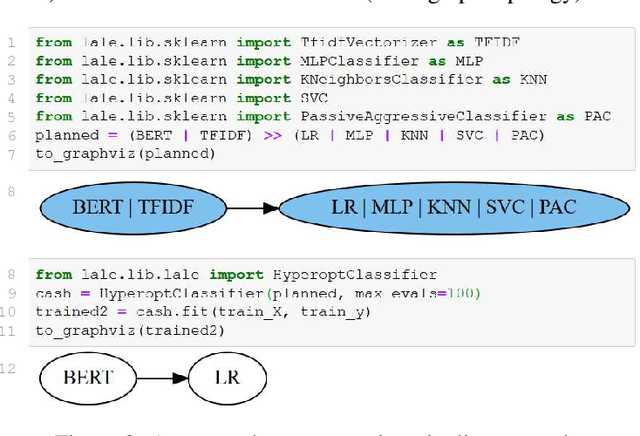
Machine-learning automation tools, ranging from humble grid-search to hyperopt, auto-sklearn, and TPOT, help explore large search spaces of possible pipelines. Unfortunately, each of these tools has a different syntax for specifying its search space, leading to lack of portability, missed relevant points, and spurious points that are inconsistent with error checks and documentation of the searchable base components. This paper proposes using types (such as enum, float, or dictionary) both for checking the correctness of, and for automatically searching over, hyperparameters and pipeline configurations. Using types for both of these purposes guarantees consistency. We present Lale, an embedded language that resembles scikit learn but provides better automation, correctness checks, and portability. Lale extends the reach of existing automation tools across data modalities (tables, text, images, time-series) and programming languages (Python, Java, R). Thus, data scientists can leverage automation while remaining in control of their work.

Extending Stan for Deep Probabilistic Programming

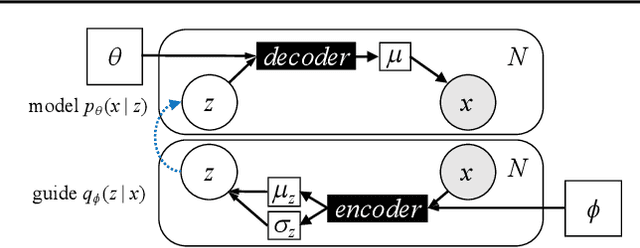
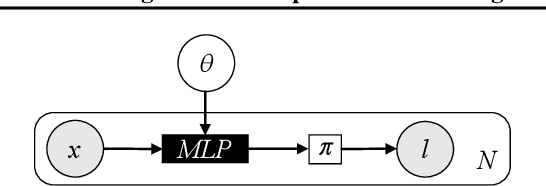
Deep probabilistic programming combines deep neural networks (for automatic hierarchical representation learning) with probabilistic models (for principled handling of uncertainty). Unfortunately, it is difficult to write deep probabilistic models, because existing programming frameworks lack concise, high-level, and clean ways to express them. To ease this task, we extend Stan, a popular high-level probabilistic programming language, to use deep neural networks written in PyTorch. Training deep probabilistic models works best with variational inference, so we also extend Stan for that. We implement these extensions by translating Stan programs to Pyro. Our translation clarifies the relationship between different families of probabilistic programming languages. Overall, our paper is a step towards making deep probabilistic programming easier.