The Teenager's Problem: Efficient Garment Decluttering With Grasp Optimization

This paper addresses the ''Teenager's Problem'': efficiently removing scattered garments from a planar surface. As grasping and transporting individual garments is highly inefficient, we propose analytical policies to select grasp locations for multiple garments using an overhead camera. Two classes of methods are considered: depth-based, which use overhead depth data to find efficient grasps, and segment-based, which use segmentation on the RGB overhead image (without requiring any depth data); grasp efficiency is measured by Objects per Transport, which denotes the average number of objects removed per trip to the laundry basket. Experiments suggest that both depth- and segment-based methods easily reduce Objects per Transport (OpT) by $20\%$; furthermore, these approaches complement each other, with combined hybrid methods yielding improvements of $34\%$. Finally, a method employing consolidation (with segmentation) is considered, which manipulates the garments on the work surface to increase OpT; this yields an improvement of $67\%$ over the baseline, though at a cost of additional physical actions.

Push-MOG: Efficient Pushing to Consolidate Polygonal Objects for Multi-Object Grasping

Recently, robots have seen rapidly increasing use in homes and warehouses to declutter by collecting objects from a planar surface and placing them into a container. While current techniques grasp objects individually, Multi-Object Grasping (MOG) can improve efficiency by increasing the average number of objects grasped per trip (OpT). However, grasping multiple objects requires the objects to be aligned and in close proximity. In this work, we propose Push-MOG, an algorithm that computes "fork pushing" actions using a parallel-jaw gripper to create graspable object clusters. In physical decluttering experiments, we find that Push-MOG enables multi-object grasps, increasing the average OpT by 34%. Code and videos will be available at https://sites.google.com/berkeley.edu/push-mog.

Agility and Target Distribution in the Dynamic Stochastic Traveling Salesman Problem

An important variant of the classic Traveling Salesman Problem (TSP) is the Dynamic TSP, in which a system with dynamic constraints is tasked with visiting a set of n target locations (in any order) in the shortest amount of time. Such tasks arise naturally in many robotic motion planning problems, particularly in exploration, surveillance and reconnaissance, and classical TSP algorithms on graphs are typically inapplicable in this setting. An important question about such problems is: if the target points are random, what is the length of the tour (either in expectation or as a concentration bound) as n grows? This problem is the Dynamic Stochastic TSP (DSTSP), and has been studied both for specific important vehicle models and for general dynamic systems; however, in general only the order of growth is known. In this work, we explore the connection between the distribution from which the targets are drawn and the dynamics of the system, yielding a more precise lower bound on tour length as well as a matching upper bound for the case of symmetric (or driftless) systems. We then extend the symmetric dynamics results to the case when the points are selected by a (non-random) adversary whose goal is to maximize the length, thus showing worst-case bounds on the tour length.

Efficient Multi-Robot Motion Planning for Unlabeled Discs in Simple Polygons

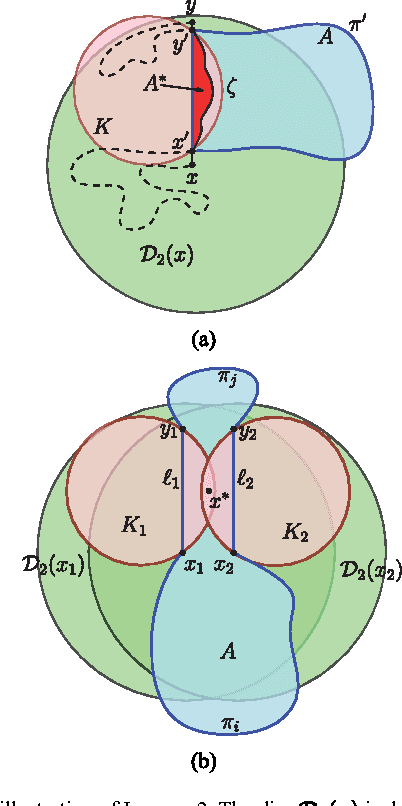
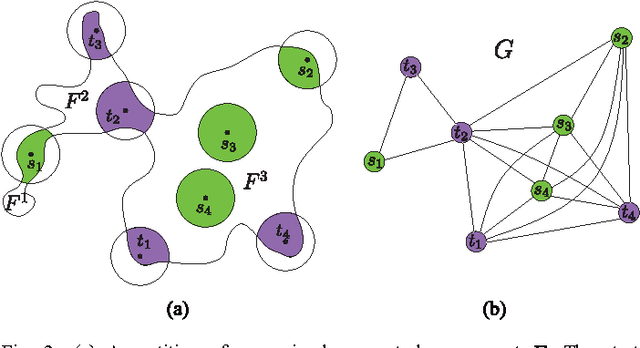
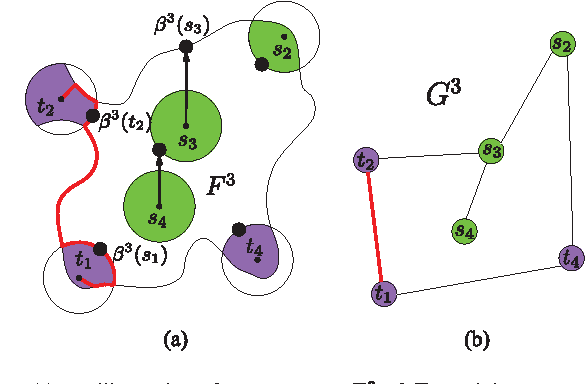
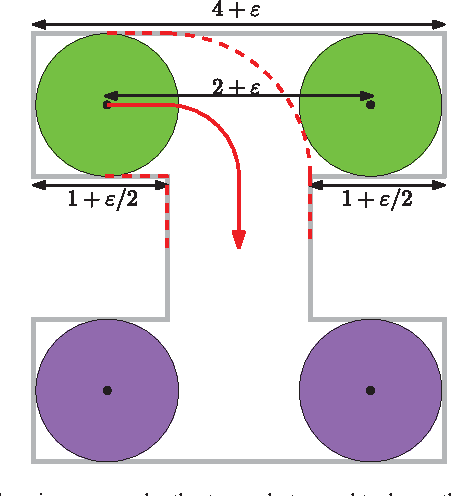
We consider the following motion-planning problem: we are given $m$ unit discs in a simple polygon with $n$ vertices, each at their own start position, and we want to move the discs to a given set of $m$ target positions. Contrary to the standard (labeled) version of the problem, each disc is allowed to be moved to any target position, as long as in the end every target position is occupied. We show that this unlabeled version of the problem can be solved in $O(n\log n+mn+m^2)$ time, assuming that the start and target positions are at least some minimal distance from each other. This is in sharp contrast to the standard (labeled) and more general multi-robot motion-planning problem for discs moving in a simple polygon, which is known to be strongly NP-hard.