Improving Faithfulness of Abstractive Summarization by Controlling Confounding Effect of Irrelevant Sentences

Lack of factual correctness is an issue that still plagues state-of-the-art summarization systems despite their impressive progress on generating seemingly fluent summaries. In this paper, we show that factual inconsistency can be caused by irrelevant parts of the input text, which act as confounders. To that end, we leverage information-theoretic measures of causal effects to quantify the amount of confounding and precisely quantify how they affect the summarization performance. Based on insights derived from our theoretical results, we design a simple multi-task model to control such confounding by leveraging human-annotated relevant sentences when available. Crucially, we give a principled characterization of data distributions where such confounding can be large thereby necessitating the use of human annotated relevant sentences to generate factual summaries. Our approach improves faithfulness scores by 20\% over strong baselines on AnswerSumm \citep{fabbri2021answersumm}, a conversation summarization dataset where lack of faithfulness is a significant issue due to the subjective nature of the task. Our best method achieves the highest faithfulness score while also achieving state-of-the-art results on standard metrics like ROUGE and METEOR. We corroborate these improvements through human evaluation.

CITADEL: Conditional Token Interaction via Dynamic Lexical Routing for Efficient and Effective Multi-Vector Retrieval

Multi-vector retrieval methods combine the merits of sparse (e.g. BM25) and dense (e.g. DPR) retrievers and have achieved state-of-the-art performance on various retrieval tasks. These methods, however, are orders of magnitude slower and need much more space to store their indices compared to their single-vector counterparts. In this paper, we unify different multi-vector retrieval models from a token routing viewpoint and propose conditional token interaction via dynamic lexical routing, namely CITADEL, for efficient and effective multi-vector retrieval. CITADEL learns to route different token vectors to the predicted lexical ``keys'' such that a query token vector only interacts with document token vectors routed to the same key. This design significantly reduces the computation cost while maintaining high accuracy. Notably, CITADEL achieves the same or slightly better performance than the previous state of the art, ColBERT-v2, on both in-domain (MS MARCO) and out-of-domain (BEIR) evaluations, while being nearly 40 times faster. Code and data are available at https://github.com/facebookresearch/dpr-scale.

FiD-Ex: Improving Sequence-to-Sequence Models for Extractive Rationale Generation

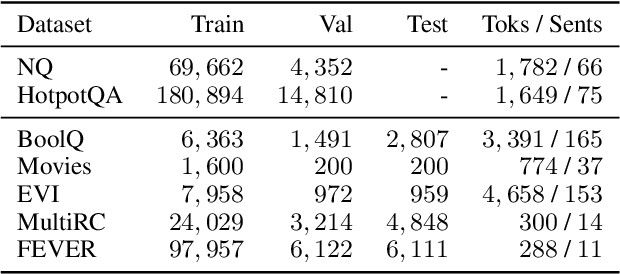
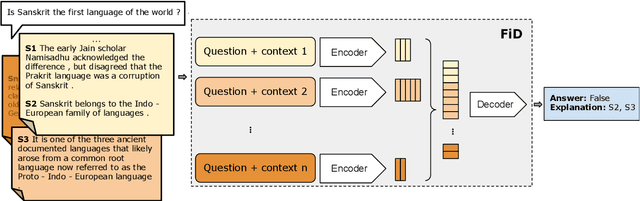
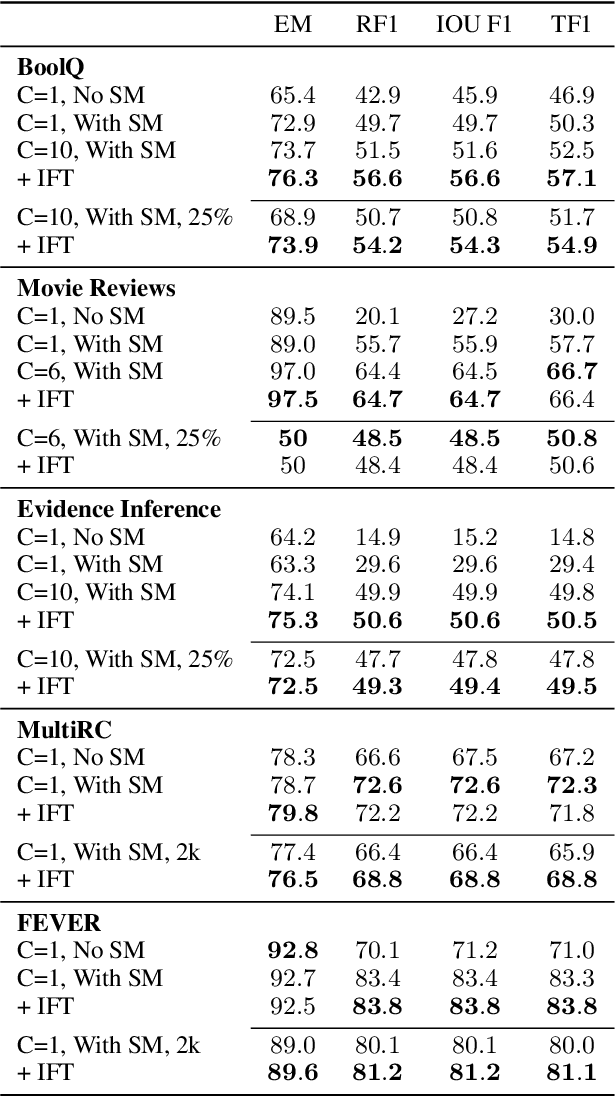
Natural language (NL) explanations of model predictions are gaining popularity as a means to understand and verify decisions made by large black-box pre-trained models, for NLP tasks such as Question Answering (QA) and Fact Verification. Recently, pre-trained sequence to sequence (seq2seq) models have proven to be very effective in jointly making predictions, as well as generating NL explanations. However, these models have many shortcomings; they can fabricate explanations even for incorrect predictions, they are difficult to adapt to long input documents, and their training requires a large amount of labeled data. In this paper, we develop FiD-Ex, which addresses these shortcomings for seq2seq models by: 1) introducing sentence markers to eliminate explanation fabrication by encouraging extractive generation, 2) using the fusion-in-decoder architecture to handle long input contexts, and 3) intermediate fine-tuning on re-structured open domain QA datasets to improve few-shot performance. FiD-Ex significantly improves over prior work in terms of explanation metrics and task accuracy, on multiple tasks from the ERASER explainability benchmark, both in the fully supervised and in the few-shot settings.

Towards Understanding the Optimal Behaviors of Deep Active Learning Algorithms

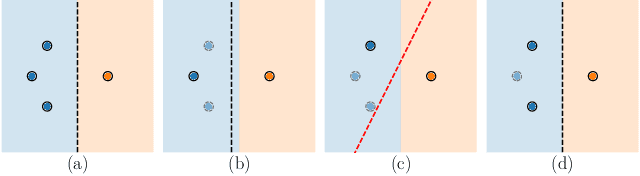
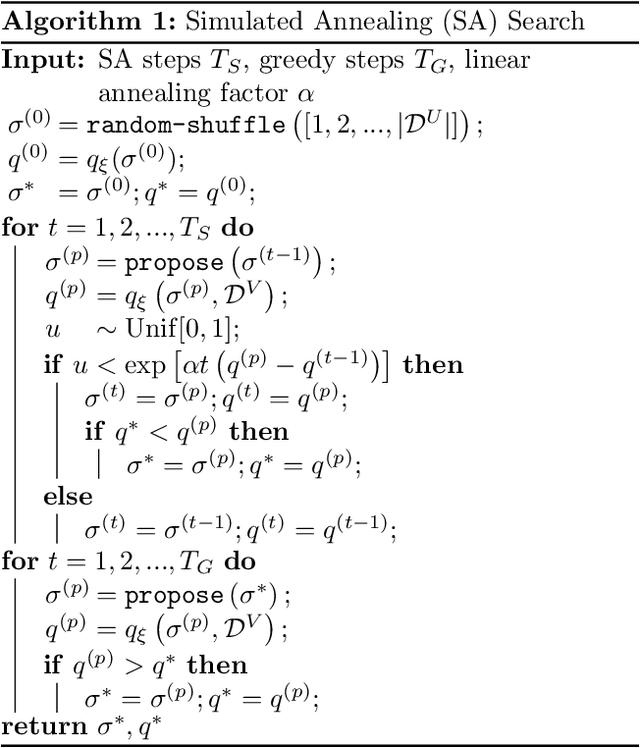
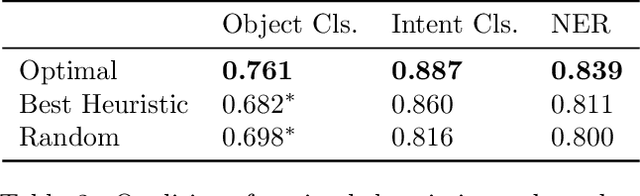
Active learning (AL) algorithms may achieve better performance with fewer data because the model guides the data selection process. While many algorithms have been proposed, there is little study on what the optimal AL algorithm looks like, which would help researchers understand where their models fall short and iterate on the design. In this paper, we present a simulated annealing algorithm to search for this optimal oracle and analyze it for several different tasks. We present several qualitative and quantitative insights into the optimal behavior and contrast this behavior with those of various heuristics. When augmented by with one particular insight, heuristics perform consistently better. We hope that our findings can better inform future active learning research. The code for the experiments is available at https://github.com/YilunZhou/optimal-active-learning.

Low-Resource Domain Adaptation for Compositional Task-Oriented Semantic Parsing

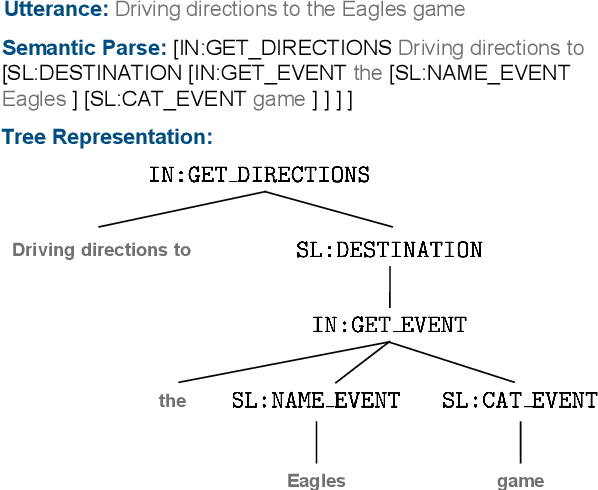
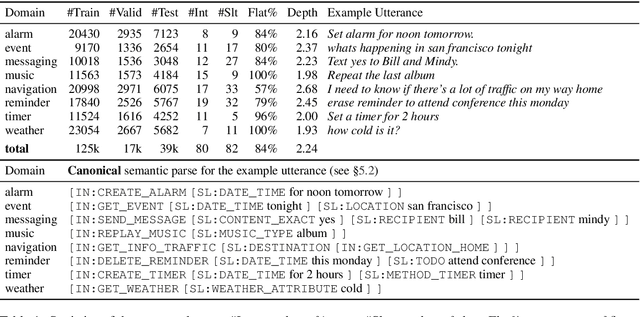
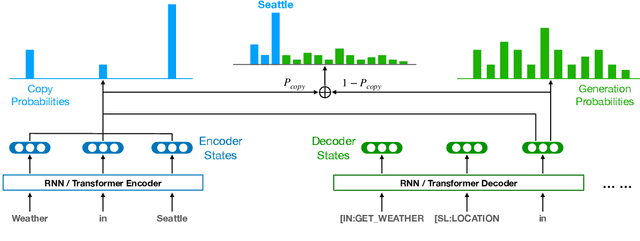
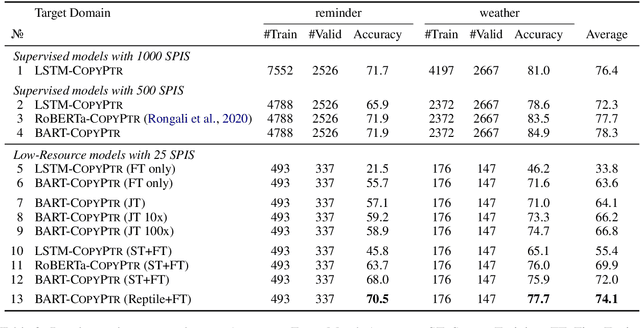
Task-oriented semantic parsing is a critical component of virtual assistants, which is responsible for understanding the user's intents (set reminder, play music, etc.). Recent advances in deep learning have enabled several approaches to successfully parse more complex queries (Gupta et al., 2018; Rongali et al.,2020), but these models require a large amount of annotated training data to parse queries on new domains (e.g. reminder, music). In this paper, we focus on adapting task-oriented semantic parsers to low-resource domains, and propose a novel method that outperforms a supervised neural model at a 10-fold data reduction. In particular, we identify two fundamental factors for low-resource domain adaptation: better representation learning and better training techniques. Our representation learning uses BART (Lewis et al., 2019) to initialize our model which outperforms encoder-only pre-trained representations used in previous work. Furthermore, we train with optimization-based meta-learning (Finn et al., 2017) to improve generalization to low-resource domains. This approach significantly outperforms all baseline methods in the experiments on a newly collected multi-domain task-oriented semantic parsing dataset (TOPv2), which we release to the public.

Direct Estimation of Difference Between Structural Equation Models in High Dimensions

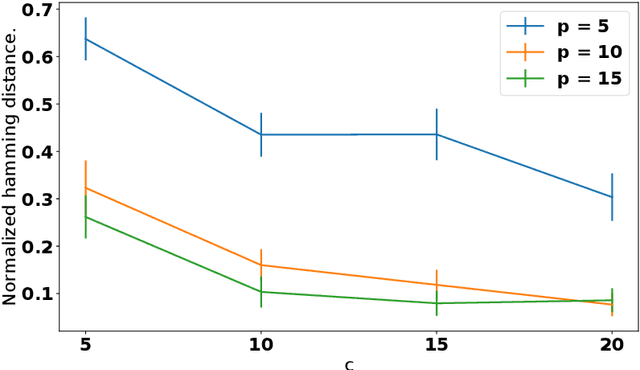
Discovering cause-effect relationships between variables from observational data is a fundamental challenge in many scientific disciplines. However, in many situations it is desirable to directly estimate the change in causal relationships across two different conditions, e.g., estimating the change in genetic expression across healthy and diseased subjects can help isolate genetic factors behind the disease. This paper focuses on the problem of directly estimating the structural difference between two causal DAGs, having the same topological ordering, given two sets of samples drawn from the individual DAGs. We present an algorithm that can recover the difference-DAG in $O(d \log p)$ samples, where $d$ is related to the number of edges in the difference-DAG. We also show that any method requires at least $\Omega(d \log p/d)$ samples to learn difference DAGs with at most $d$ parents per node. We validate our theoretical results with synthetic experiments and show that our method out-performs the state-of-the-art.

Minimax bounds for structured prediction

Structured prediction can be considered as a generalization of many standard supervised learning tasks, and is usually thought as a simultaneous prediction of multiple labels. One standard approach is to maximize a score function on the space of labels, which decomposes as a sum of unary and pairwise potentials, each depending on one or two specific labels, respectively. For this approach, several learning and inference algorithms have been proposed over the years, ranging from exact to approximate methods while balancing the computational complexity. However, in contrast to binary and multiclass classification, results on the necessary number of samples for achieving learning is still limited, even for a specific family of predictors such as factor graphs. In this work, we provide minimax bounds for a class of factor-graph inference models for structured prediction. That is, we characterize the necessary sample complexity for any conceivable algorithm to achieve learning of factor-graph predictors.

Learning Maximum-A-Posteriori Perturbation Models for Structured Prediction in Polynomial Time

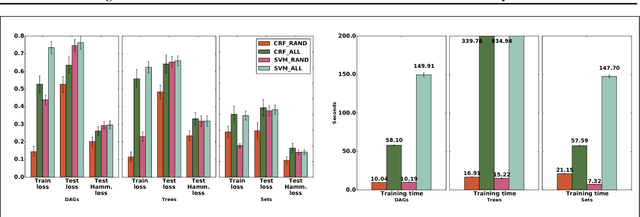
MAP perturbation models have emerged as a powerful framework for inference in structured prediction. Such models provide a way to efficiently sample from the Gibbs distribution and facilitate predictions that are robust to random noise. In this paper, we propose a provably polynomial time randomized algorithm for learning the parameters of perturbed MAP predictors. Our approach is based on minimizing a novel Rademacher-based generalization bound on the expected loss of a perturbed MAP predictor, which can be computed in polynomial time. We obtain conditions under which our randomized learning algorithm can guarantee generalization to unseen examples.

Learning Sparse Polymatrix Games in Polynomial Time and Sample Complexity

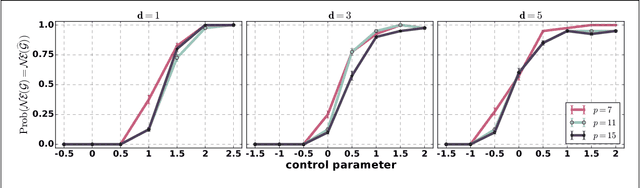
We consider the problem of learning sparse polymatrix games from observations of strategic interactions. We show that a polynomial time method based on $\ell_{1,2}$-group regularized logistic regression recovers a game, whose Nash equilibria are the $\epsilon$-Nash equilibria of the game from which the data was generated (true game), in $\mathcal{O}(m^4 d^4 \log (pd))$ samples of strategy profiles --- where $m$ is the maximum number of pure strategies of a player, $p$ is the number of players, and $d$ is the maximum degree of the game graph. Under slightly more stringent separability conditions on the payoff matrices of the true game, we show that our method learns a game with the exact same Nash equilibria as the true game. We also show that $\Omega(d \log (pm))$ samples are necessary for any method to consistently recover a game, with the same Nash-equilibria as the true game, from observations of strategic interactions. We verify our theoretical results through simulation experiments.

Learning linear structural equation models in polynomial time and sample complexity

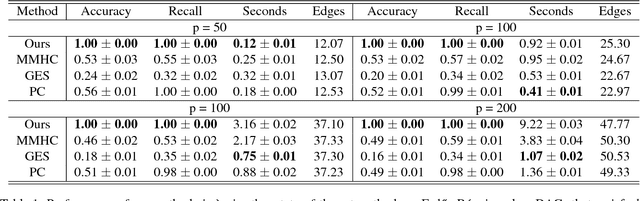
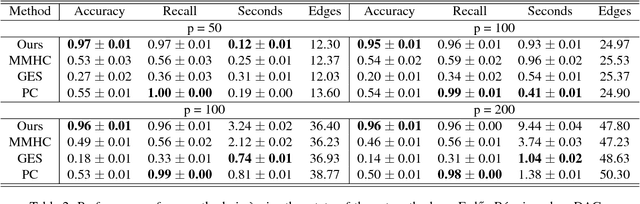
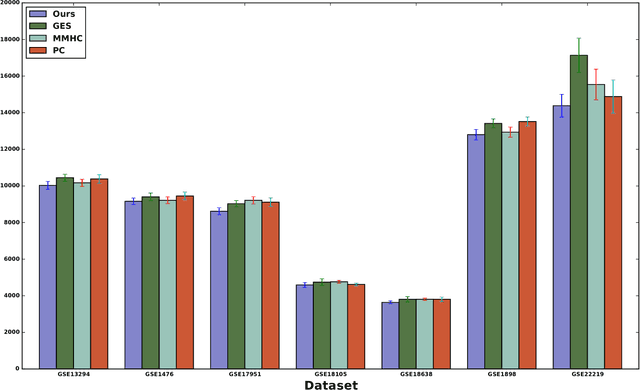
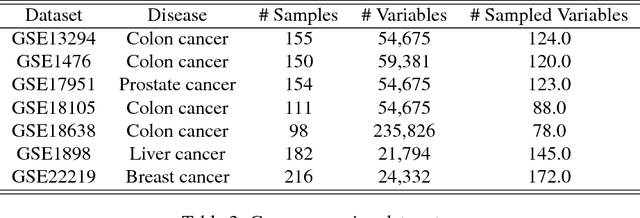
The problem of learning structural equation models (SEMs) from data is a fundamental problem in causal inference. We develop a new algorithm --- which is computationally and statistically efficient and works in the high-dimensional regime --- for learning linear SEMs from purely observational data with arbitrary noise distribution. We consider three aspects of the problem: identifiability, computational efficiency, and statistical efficiency. We show that when data is generated from a linear SEM over $p$ nodes and maximum degree $d$, our algorithm recovers the directed acyclic graph (DAG) structure of the SEM under an identifiability condition that is more general than those considered in the literature, and without faithfulness assumptions. In the population setting, our algorithm recovers the DAG structure in $\mathcal{O}(p(d^2 + \log p))$ operations. In the finite sample setting, if the estimated precision matrix is sparse, our algorithm has a smoothed complexity of $\widetilde{\mathcal{O}}(p^3 + pd^7)$, while if the estimated precision matrix is dense, our algorithm has a smoothed complexity of $\widetilde{\mathcal{O}}(p^5)$. For sub-Gaussian noise, we show that our algorithm has a sample complexity of $\mathcal{O}(\frac{d^8}{\varepsilon^2} \log (\frac{p}{\sqrt{\delta}}))$ to achieve $\varepsilon$ element-wise additive error with respect to the true autoregression matrix with probability at most $1 - \delta$, while for noise with bounded $(4m)$-th moment, with $m$ being a positive integer, our algorithm has a sample complexity of $\mathcal{O}(\frac{d^8}{\varepsilon^2} (\frac{p^2}{\delta})^{1/m})$.