Learning stochastic multiscale models through normalizing flows

Many systems in physics, engineering, and biology exhibit multiscale stochastic dynamics, where low-dimensional slow variables evolve under the influence of high-dimensional fast processes. In practice, observations are often limited to a single trajectory of the slow component, while the fast dynamics remain unobserved, making statistical learning challenging. Approaches based on partial differential equations (PDE), such as Fokker-Planck formulations, aim to characterize the evolution of probability densities, typically requiring dense space-time data or grid-based solvers. In contrast, we adopt a trajectory-based perspective and develop a data-driven framework for learning effective stochastic dynamics from a single observed path. We model the dynamics by coupled multiscale stochastic differential equations (SDEs) and first obtain a principled model reduction through stochastic averaging. Unlike generic model reduction techniques such as PCA, this respects the dynamical structure of the original system and explicitly incorporates the interaction between slow and fast scales. A central challenge, however, is that the reduced model depends on the invariant distribution of the fast process, which is a solution to an intractable and often unknown PDE. We introduce a novel learning framework that parameterizes the invariant distribution using normalizing flows, enabling expressive density modeling in the latent fast-variable space. The flow is trained end-to-end by optimizing a penalized likelihood objective induced by the reduced stochastic dynamics. Furthermore, we develop a Bayesian variational inference procedure for uncertainty quantification, employing a second normalizing flow to approximate the posterior distribution over model parameters. This yields a scalable approach to capturing epistemic uncertainty in multiscale systems.

Variational Smoothing and Inference for SDEs from Sparse Data with Dynamic Neural Flows

Stochastic differential equations (SDEs) provide a flexible framework for modeling temporal dynamics in partially observed systems. A central task is to calibrate such models from data, which requires inferring latent trajectories and parameters from sparse, noisy observations. Classical smoothing methods for this problem are often limited by path degeneracy and poor scalability. In this work, we developed a novel method based on characterization of the posterior SDE in terms of conditional backward-in-time score defined as the gradient of a function solving a Kolmogorov backward equation with multiplicative updates at observation times. We learn this conditional score using neural networks trained to satisfy both the governing PDE and the observation-induced jump conditions, thereby integrating continuous-time dynamics with discrete Bayesian updates. The resulting score induces a posterior SDE with the same diffusion coefficient but a modified drift, enabling efficient posterior trajectory sampling. We further derive a likelihood-based objective for learning the SDE parameters, yielding an evidence lower bound (ELBO) for joint state smoothing and parameter estimation. This leads to a variational EM-style procedure, where the neural conditional score is optimized to approximate the smoothing distribution, followed by a maximization step over the SDE parameters using samples from the induced posterior. Experiments on nonlinear systems demonstrate accurate and stable inference with a very few observations demonstrating significant improved scalability compared to classical MCMC methods.

Nonparametric learning of covariate-based Markov jump processes using RKHS techniques

We propose a novel nonparametric approach for linking covariates to Continuous Time Markov Chains (CTMCs) using the mathematical framework of Reproducing Kernel Hilbert Spaces (RKHS). CTMCs provide a robust framework for modeling transitions across clinical or behavioral states, but traditional multistate models often rely on linear relationships. In contrast, we use a generalized Representer Theorem to enable tractable inference in functional space. For the Frequentist version, we apply normed square penalties, while for the Bayesian version, we explore sparsity inducing spike and slab priors. Due to the computational challenges posed by high-dimensional spaces, we successfully adapt the Expectation Maximization Variable Selection (EMVS) algorithm to efficiently identify the posterior mode. We demonstrate the effectiveness of our method through extensive simulation studies and an application to follicular cell lymphoma data. Our performance metrics include the normalized difference between estimated and true nonlinear transition functions, as well as the difference in the probability of getting absorbed in one the final states, capturing the ability of our approach to predict long-term behaviors.

Optimal Learning via Moderate Deviations Theory

This paper proposes a statistically optimal approach for learning a function value using a confidence interval in a wide range of models, including general non-parametric estimation of an expected loss described as a stochastic programming problem or various SDE models. More precisely, we develop a systematic construction of highly accurate confidence intervals by using a moderate deviation principle-based approach. It is shown that the proposed confidence intervals are statistically optimal in the sense that they satisfy criteria regarding exponential accuracy, minimality, consistency, mischaracterization probability, and eventual uniformly most accurate (UMA) property. The confidence intervals suggested by this approach are expressed as solutions to robust optimization problems, where the uncertainty is expressed via the underlying moderate deviation rate function induced by the data-generating process. We demonstrate that for many models these optimization problems admit tractable reformulations as finite convex programs even when they are infinite-dimensional.

Infinite-dimensional optimization and Bayesian nonparametric learning of stochastic differential equations

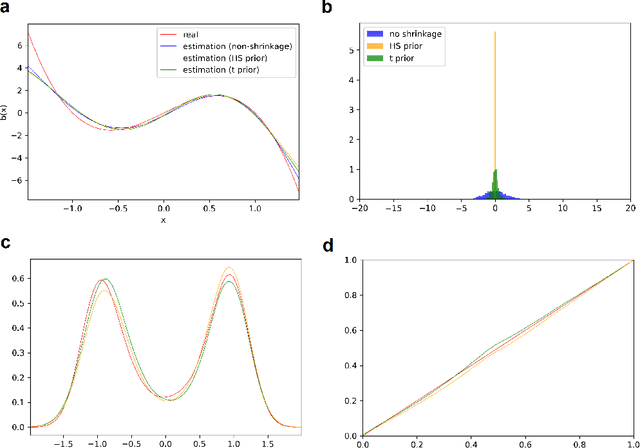
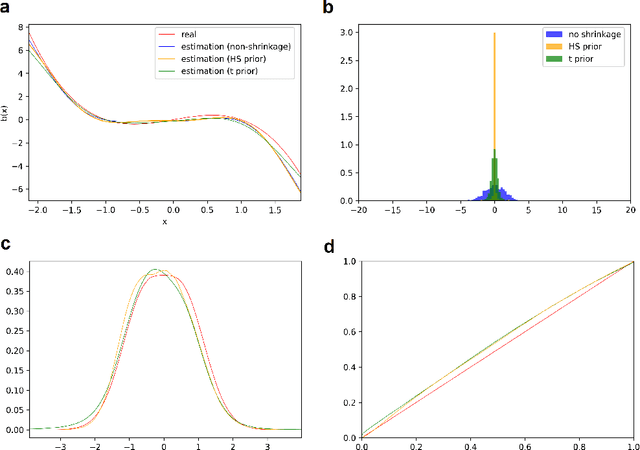
The paper has two major themes. The first part of the paper establishes certain general results for infinite-dimensional optimization problems on Hilbert spaces. These results cover the classical representer theorem and many of its variants as special cases and offer a wider scope of applications. The second part of the paper then develops a systematic approach for learning the drift function of a stochastic differential equation by integrating the results of the first part with Bayesian hierarchical framework. Importantly, our Baysian approach incorporates low-cost sparse learning through proper use of shrinkage priors while allowing proper quantification of uncertainty through posterior distributions. Several examples at the end illustrate the accuracy of our learning scheme.

Context-Aware Design of Cyber-Physical Human Systems

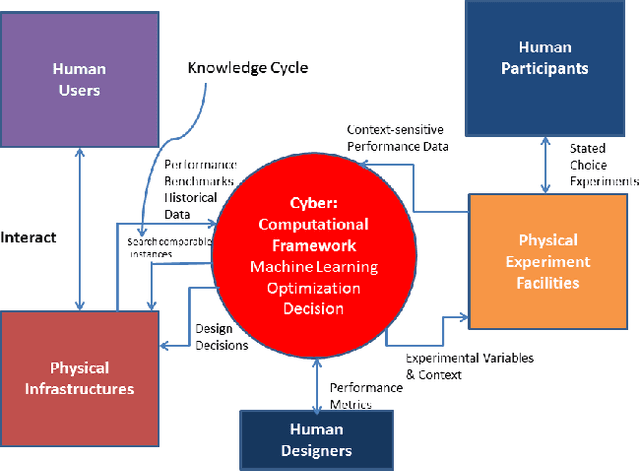
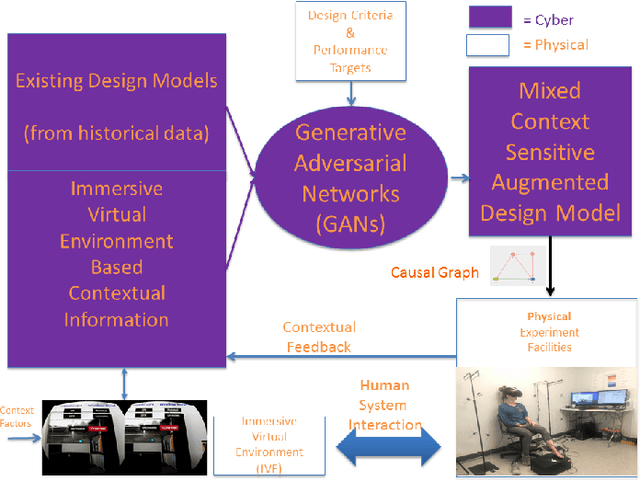
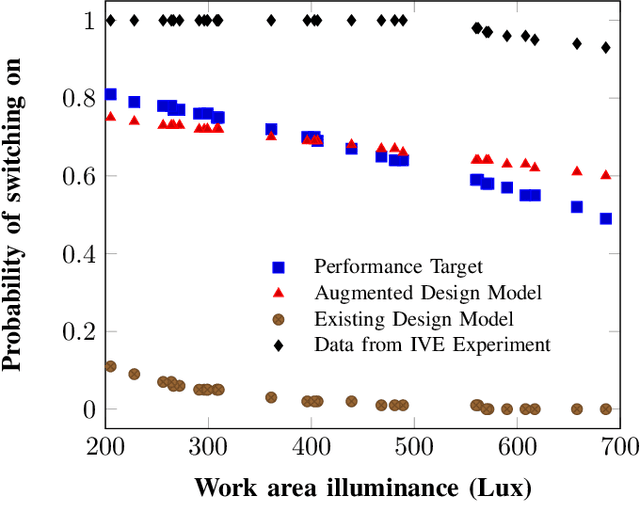
Recently, it has been widely accepted by the research community that interactions between humans and cyber-physical infrastructures have played a significant role in determining the performance of the latter. The existing paradigm for designing cyber-physical systems for optimal performance focuses on developing models based on historical data. The impacts of context factors driving human system interaction are challenging and are difficult to capture and replicate in existing design models. As a result, many existing models do not or only partially address those context factors of a new design owing to the lack of capabilities to capture the context factors. This limitation in many existing models often causes performance gaps between predicted and measured results. We envision a new design environment, a cyber-physical human system (CPHS) where decision-making processes for physical infrastructures under design are intelligently connected to distributed resources over cyberinfrastructure such as experiments on design features and empirical evidence from operations of existing instances. The framework combines existing design models with context-aware design-specific data involving human-infrastructure interactions in new designs, using a machine learning approach to create augmented design models with improved predictive powers.

A variational approach to path estimation and parameter inference of hidden diffusion processes

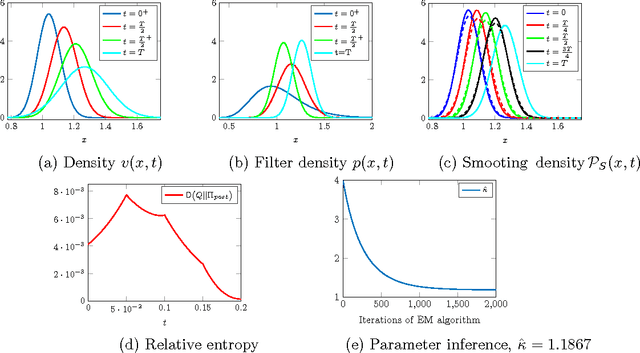
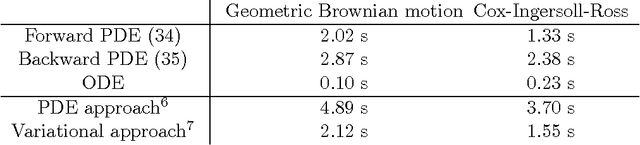
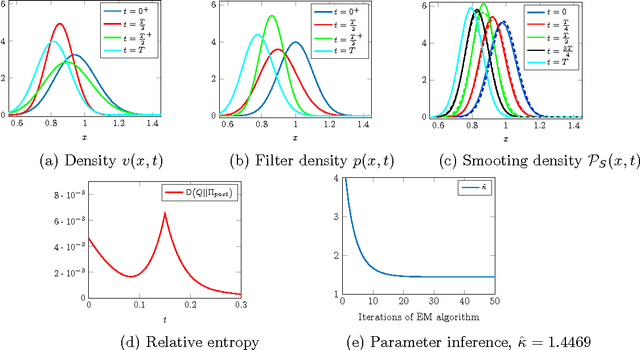
We consider a hidden Markov model, where the signal process, given by a diffusion, is only indirectly observed through some noisy measurements. The article develops a variational method for approximating the hidden states of the signal process given the full set of observations. This, in particular, leads to systematic approximations of the smoothing densities of the signal process. The paper then demonstrates how an efficient inference scheme, based on this variational approach to the approximation of the hidden states, can be designed to estimate the unknown parameters of stochastic differential equations. Two examples at the end illustrate the efficacy and the accuracy of the presented method.