Revisit CP Tensor Decomposition: Statistical Optimality and Fast Convergence

Canonical Polyadic (CP) tensor decomposition is a fundamental technique for analyzing high-dimensional tensor data. While the Alternating Least Squares (ALS) algorithm is widely used for computing CP decomposition due to its simplicity and empirical success, its theoretical foundation, particularly regarding statistical optimality and convergence behavior, remain underdeveloped, especially in noisy, non-orthogonal, and higher-rank settings. In this work, we revisit CP tensor decomposition from a statistical perspective and provide a comprehensive theoretical analysis of ALS under a signal-plus-noise model. We establish non-asymptotic, minimax-optimal error bounds for tensors of general order, dimensions, and rank, assuming suitable initialization. To enable such initialization, we propose Tucker-based Approximation with Simultaneous Diagonalization (TASD), a robust method that improves stability and accuracy in noisy regimes. Combined with ALS, TASD yields a statistically consistent estimator. We further analyze the convergence dynamics of ALS, identifying a two-phase pattern-initial quadratic convergence followed by linear refinement. We further show that in the rank-one setting, ALS with an appropriately chosen initialization attains optimal error within just one or two iterations.

Optimal community detection in dense bipartite graphs

We consider the problem of detecting a community of densely connected vertices in a high-dimensional bipartite graph of size $n_1 \times n_2$. Under the null hypothesis, the observed graph is drawn from a bipartite Erd\H{o}s-Renyi distribution with connection probability $p_0$. Under the alternative hypothesis, there exists an unknown bipartite subgraph of size $k_1 \times k_2$ in which edges appear with probability $p_1 = p_0 + \delta$ for some $\delta > 0$, while all other edges outside the subgraph appear with probability $p_0$. Specifically, we provide non-asymptotic upper and lower bounds on the smallest signal strength $\delta^*$ that is both necessary and sufficient to ensure the existence of a test with small enough type one and type two errors. We also derive novel minimax-optimal tests achieving these fundamental limits when the underlying graph is sufficiently dense. Our proposed tests involve a combination of hard-thresholded nonlinear statistics of the adjacency matrix, the analysis of which may be of independent interest. In contrast with previous work, our non-asymptotic upper and lower bounds match for any configuration of $n_1,n_2, k_1,k_2$.

Sparse Signal Detection in Heteroscedastic Gaussian Sequence Models: Sharp Minimax Rates

Given a heterogeneous Gaussian sequence model with unknown mean $\theta \in \mathbb R^d$ and known covariance matrix $\Sigma = \operatorname{diag}(\sigma_1^2,\dots, \sigma_d^2)$, we study the signal detection problem against sparse alternatives, for known sparsity $s$. Namely, we characterize how large $\epsilon^*>0$ should be, in order to distinguish with high probability the null hypothesis $\theta=0$ from the alternative composed of $s$-sparse vectors in $\mathbb R^d$, separated from $0$ in $L^t$ norm ($t \geq 1$) by at least $\epsilon^*$. We find minimax upper and lower bounds over the minimax separation radius $\epsilon^*$ and prove that they are always matching. We also derive the corresponding minimax tests achieving these bounds. Our results reveal new phase transitions regarding the behavior of $\epsilon^*$ with respect to the level of sparsity, to the $L^t$ metric, and to the heteroscedasticity profile of $\Sigma$. In the case of the Euclidean (i.e. $L^2$) separation, we bridge the remaining gaps in the literature.

Benign overfitting and adaptive nonparametric regression

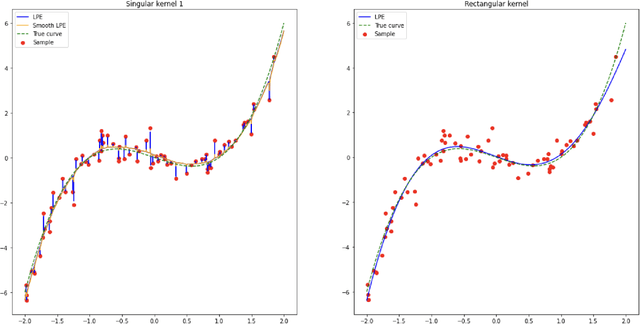
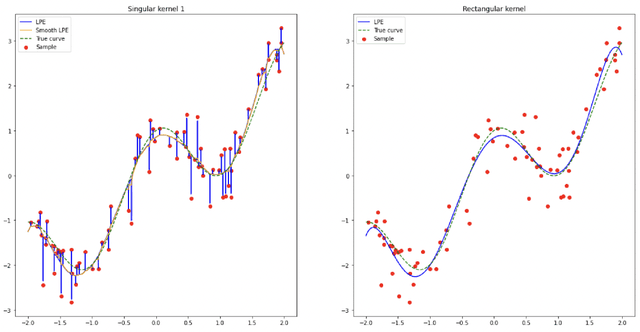
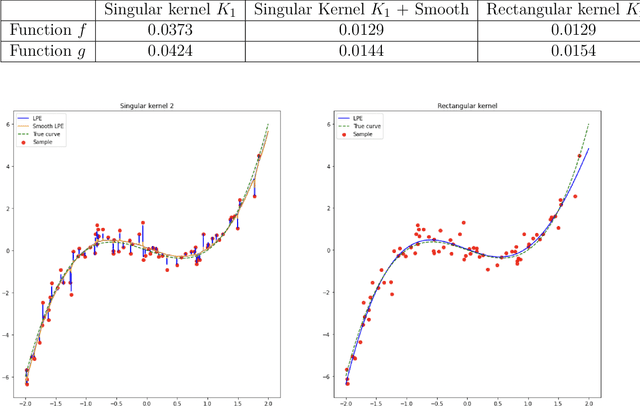
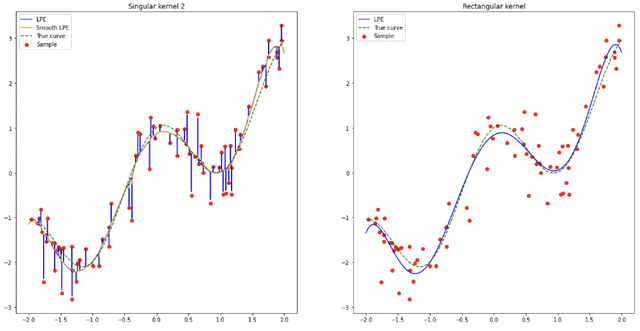
In the nonparametric regression setting, we construct an estimator which is a continuous function interpolating the data points with high probability, while attaining minimax optimal rates under mean squared risk on the scale of H\"older classes adaptively to the unknown smoothness.

Robust Estimation of Discrete Distributions under Local Differential Privacy

Although robust learning and local differential privacy are both widely studied fields of research, combining the two settings is an almost unexplored topic. We consider the problem of estimating a discrete distribution in total variation from $n$ contaminated data batches under a local differential privacy constraint. A fraction $1-\epsilon$ of the batches contain $k$ i.i.d. samples drawn from a discrete distribution $p$ over $d$ elements. To protect the users' privacy, each of the samples is privatized using an $\alpha$-locally differentially private mechanism. The remaining $\epsilon n $ batches are an adversarial contamination. The minimax rate of estimation under contamination alone, with no privacy, is known to be $\epsilon/\sqrt{k}+\sqrt{d/kn}$, up to a $\sqrt{\log(1/\epsilon)}$ factor. Under the privacy constraint alone, the minimax rate of estimation is $\sqrt{d^2/\alpha^2 kn}$. We show that combining the two constraints leads to a minimax estimation rate of $\epsilon\sqrt{d/\alpha^2 k}+\sqrt{d^2/\alpha^2 kn}$ up to a $\sqrt{\log(1/\epsilon)}$ factor, larger than the sum of the two separate rates. We provide a polynomial-time algorithm achieving this bound, as well as a matching information theoretic lower bound.