Testing GPT-4 with Wolfram Alpha and Code Interpreter plug-ins on math and science problems

This report describes a test of the large language model GPT-4 with the Wolfram Alpha and the Code Interpreter plug-ins on 105 original problems in science and math, at the high school and college levels, carried out in June-August 2023. Our tests suggest that the plug-ins significantly enhance GPT's ability to solve these problems. Having said that, there are still often "interface" failures; that is, GPT often has trouble formulating problems in a way that elicits useful answers from the plug-ins. Fixing these interface failures seems like a central challenge in making GPT a reliable tool for college-level calculation problems.

A very preliminary analysis of DALL-E 2

The DALL-E 2 system generates original synthetic images corresponding to an input text as caption. We report here on the outcome of fourteen tests of this system designed to assess its common sense, reasoning and ability to understand complex texts. All of our prompts were intentionally much more challenging than the typical ones that have been showcased in recent weeks. Nevertheless, for 5 out of the 14 prompts, at least one of the ten images fully satisfied our requests. On the other hand, on no prompt did all of the ten images satisfy our requests.

Efficient Learning of Non-Interacting Fermion Distributions

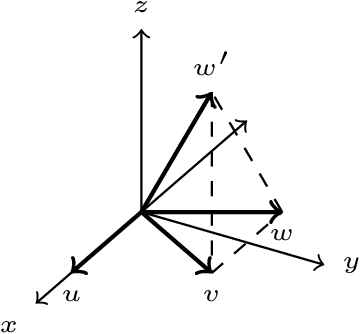
We give an efficient classical algorithm that recovers the distribution of a non-interacting fermion state over the computational basis. For a system of $n$ non-interacting fermions and $m$ modes, we show that $O(m^2 n^4 \log(m/\delta)/ \varepsilon^4)$ samples and $O(m^4 n^4 \log(m/\delta)/ \varepsilon^4)$ time are sufficient to learn the original distribution to total variation distance $\varepsilon$ with probability $1 - \delta$. Our algorithm empirically estimates the one- and two-mode correlations and uses them to reconstruct a succinct description of the entire distribution efficiently.

Online Learning of Quantum States

Suppose we have many copies of an unknown $n$-qubit state $\rho$. We measure some copies of $\rho$ using a known two-outcome measurement $E_{1}$, then other copies using a measurement $E_{2}$, and so on. At each stage $t$, we generate a current hypothesis $\sigma_{t}$ about the state $\rho$, using the outcomes of the previous measurements. We show that it is possible to do this in a way that guarantees that $|\operatorname{Tr}(E_{i} \sigma_{t}) - \operatorname{Tr}(E_{i}\rho) |$, the error in our prediction for the next measurement, is at least $\varepsilon$ at most $\operatorname{O}\!\left(n / \varepsilon^2 \right) $ times. Even in the "non-realizable" setting---where there could be arbitrary noise in the measurement outcomes---we show how to output hypothesis states that do significantly worse than the best possible states at most $\operatorname{O}\!\left(\sqrt {Tn}\right) $ times on the first $T$ measurements. These results generalize a 2007 theorem by Aaronson on the PAC-learnability of quantum states, to the online and regret-minimization settings. We give three different ways to prove our results---using convex optimization, quantum postselection, and sequential fat-shattering dimension---which have different advantages in terms of parameters and portability.

Experimental learning of quantum states

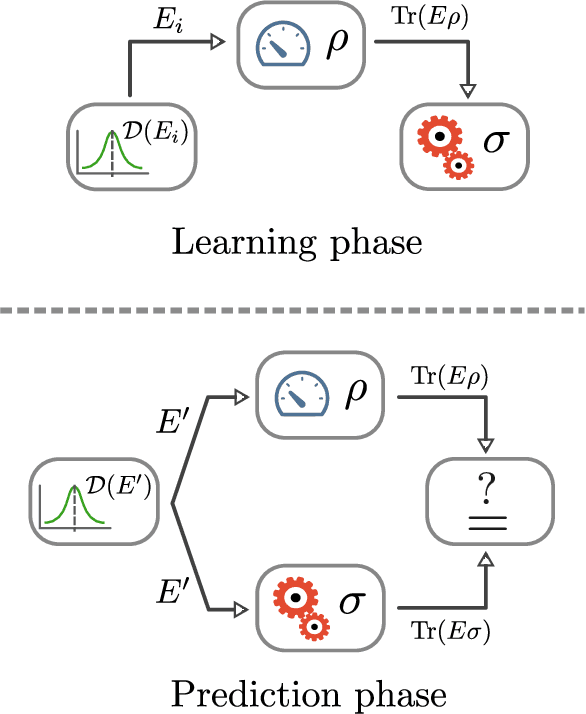
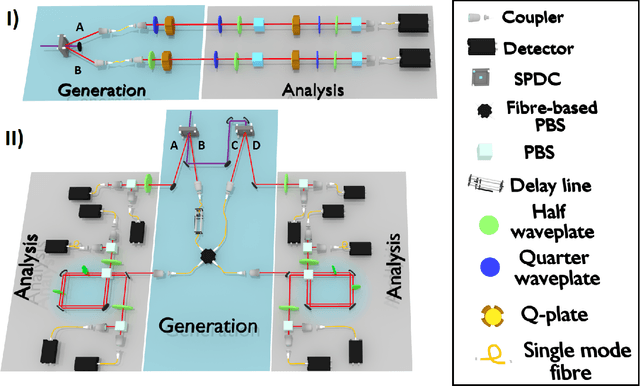
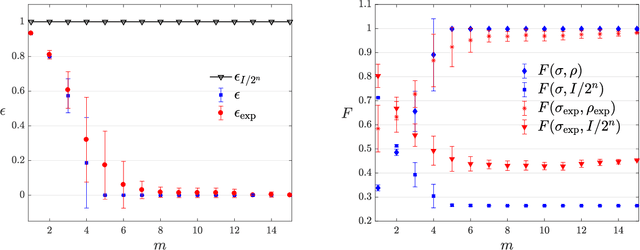
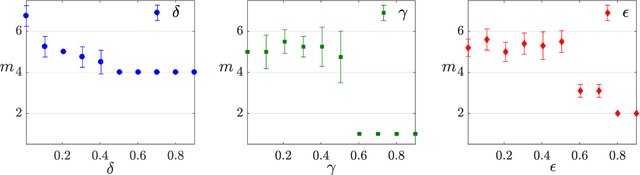
The number of parameters describing a quantum state is well known to grow exponentially with the number of particles. This scaling clearly limits our ability to do tomography to systems with no more than a few qubits and has been used to argue against the universal validity of quantum mechanics itself. However, from a computational learning theory perspective, it can be shown that, in a probabilistic setting, quantum states can be approximately learned using only a linear number of measurements. Here we experimentally demonstrate this linear scaling in optical systems with up to 6 qubits. Our results highlight the power of computational learning theory to investigate quantum information, provide the first experimental demonstration that quantum states can be "probably approximately learned" with access to a number of copies of the state that scales linearly with the number of qubits, and pave the way to probing quantum states at new, larger scales.

Quantum POMDPs

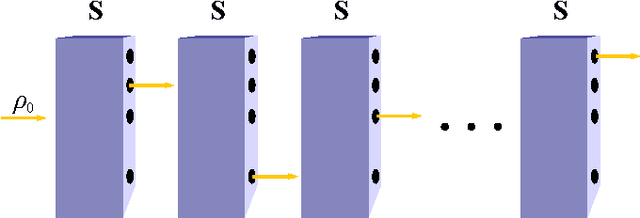
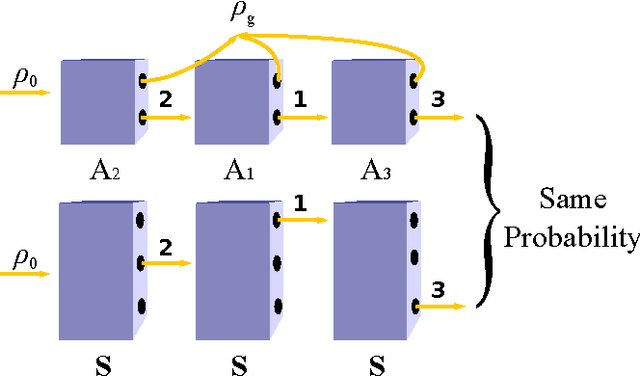
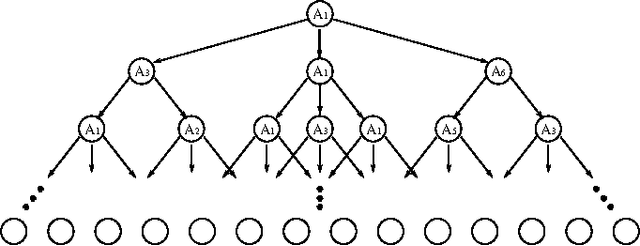
We present quantum observable Markov decision processes (QOMDPs), the quantum analogues of partially observable Markov decision processes (POMDPs). In a QOMDP, an agent's state is represented as a quantum state and the agent can choose a superoperator to apply. This is similar to the POMDP belief state, which is a probability distribution over world states and evolves via a stochastic matrix. We show that the existence of a policy of at least a certain value has the same complexity for QOMDPs and POMDPs in the polynomial and infinite horizon cases. However, we also prove that the existence of a policy that can reach a goal state is decidable for goal POMDPs and undecidable for goal QOMDPs.