Proximal Implicit ODE Solvers for Accelerating Learning Neural ODEs

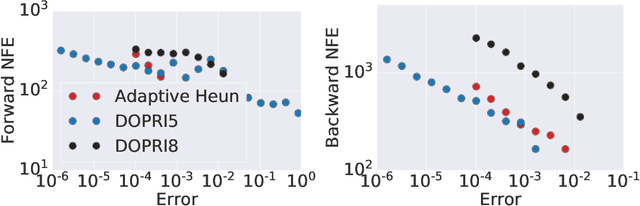
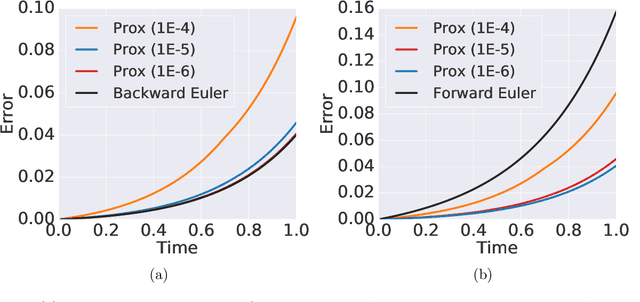
Learning neural ODEs often requires solving very stiff ODE systems, primarily using explicit adaptive step size ODE solvers. These solvers are computationally expensive, requiring the use of tiny step sizes for numerical stability and accuracy guarantees. This paper considers learning neural ODEs using implicit ODE solvers of different orders leveraging proximal operators. The proximal implicit solver consists of inner-outer iterations: the inner iterations approximate each implicit update step using a fast optimization algorithm, and the outer iterations solve the ODE system over time. The proximal implicit ODE solver guarantees superiority over explicit solvers in numerical stability and computational efficiency. We validate the advantages of proximal implicit solvers over existing popular neural ODE solvers on various challenging benchmark tasks, including learning continuous-depth graph neural networks and continuous normalizing flows.

Graph-based Active Learning for Semi-supervised Classification of SAR Data

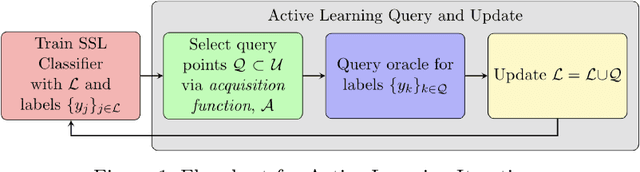
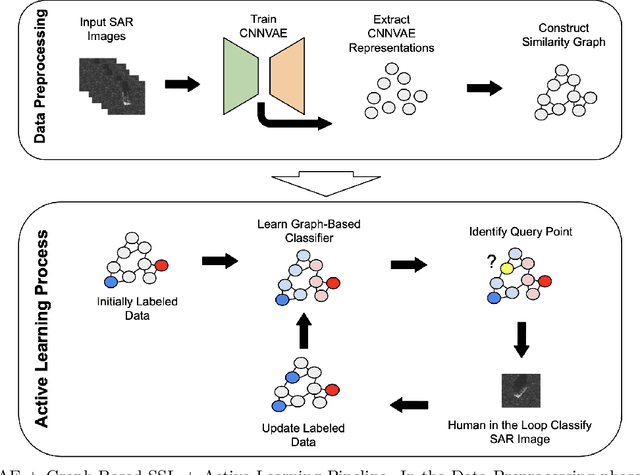
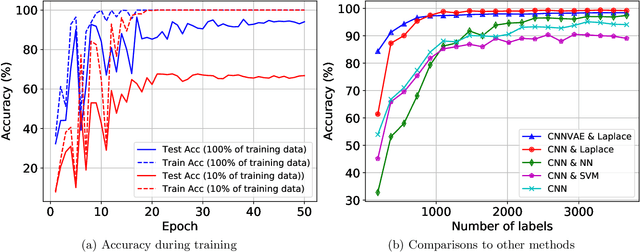
We present a novel method for classification of Synthetic Aperture Radar (SAR) data by combining ideas from graph-based learning and neural network methods within an active learning framework. Graph-based methods in machine learning are based on a similarity graph constructed from the data. When the data consists of raw images composed of scenes, extraneous information can make the classification task more difficult. In recent years, neural network methods have been shown to provide a promising framework for extracting patterns from SAR images. These methods, however, require ample training data to avoid overfitting. At the same time, such training data are often unavailable for applications of interest, such as automatic target recognition (ATR) and SAR data. We use a Convolutional Neural Network Variational Autoencoder (CNNVAE) to embed SAR data into a feature space, and then construct a similarity graph from the embedded data and apply graph-based semi-supervised learning techniques. The CNNVAE feature embedding and graph construction requires no labeled data, which reduces overfitting and improves the generalization performance of graph learning at low label rates. Furthermore, the method easily incorporates a human-in-the-loop for active learning in the data-labeling process. We present promising results and compare them to other standard machine learning methods on the Moving and Stationary Target Acquisition and Recognition (MSTAR) dataset for ATR with small amounts of labeled data.

Efficient and Reliable Overlay Networks for Decentralized Federated Learning

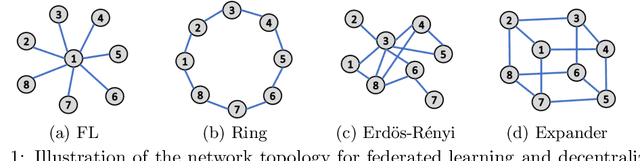
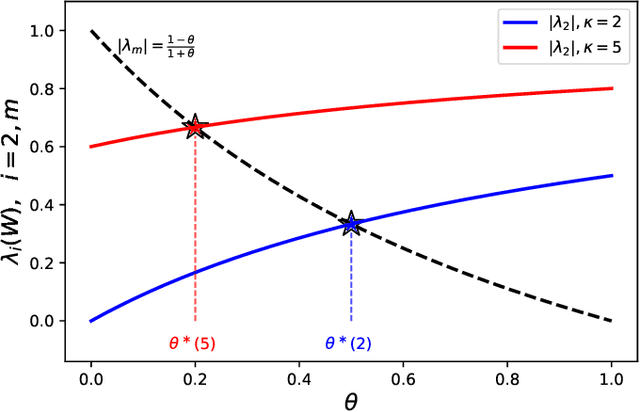
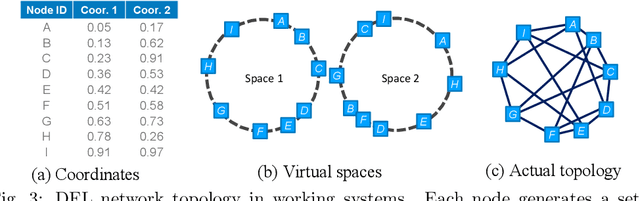
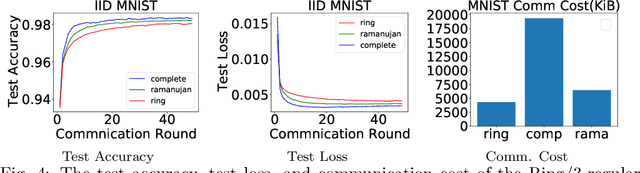
We propose near-optimal overlay networks based on $d$-regular expander graphs to accelerate decentralized federated learning (DFL) and improve its generalization. In DFL a massive number of clients are connected by an overlay network, and they solve machine learning problems collaboratively without sharing raw data. Our overlay network design integrates spectral graph theory and the theoretical convergence and generalization bounds for DFL. As such, our proposed overlay networks accelerate convergence, improve generalization, and enhance robustness to clients failures in DFL with theoretical guarantees. Also, we present an efficient algorithm to convert a given graph to a practical overlay network and maintaining the network topology after potential client failures. We numerically verify the advantages of DFL with our proposed networks on various benchmark tasks, ranging from image classification to language modeling using hundreds of clients.

Model-Change Active Learning in Graph-Based Semi-Supervised Learning

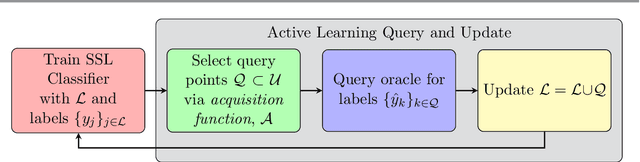
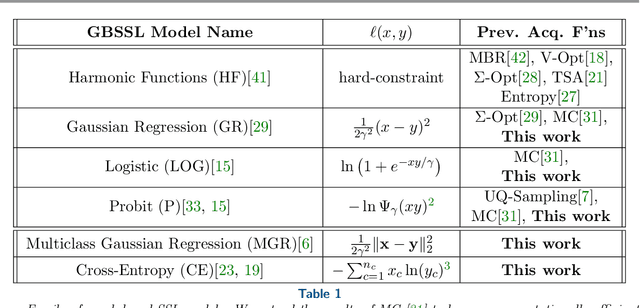
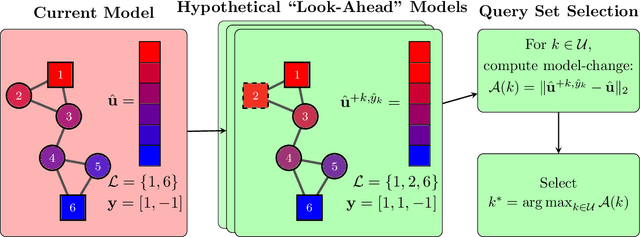
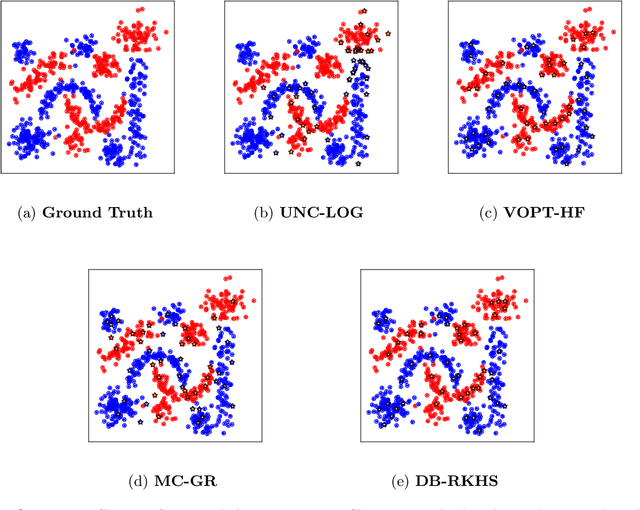
Active learning in semi-supervised classification involves introducing additional labels for unlabelled data to improve the accuracy of the underlying classifier. A challenge is to identify which points to label to best improve performance while limiting the number of new labels. "Model-change" active learning quantifies the resulting change incurred in the classifier by introducing the additional label(s). We pair this idea with graph-based semi-supervised learning methods, that use the spectrum of the graph Laplacian matrix, which can be truncated to avoid prohibitively large computational and storage costs. We consider a family of convex loss functions for which the acquisition function can be efficiently approximated using the Laplace approximation of the posterior distribution. We show a variety of multiclass examples that illustrate improved performance over prior state-of-art.

An Analysis of COVID-19 Knowledge Graph Construction and Applications

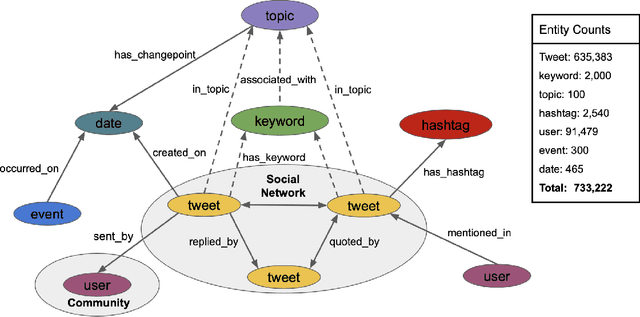
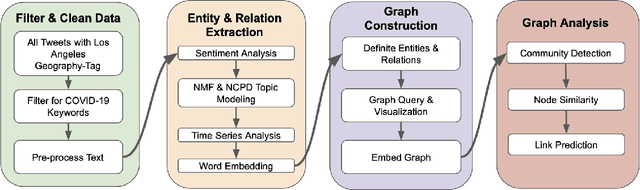
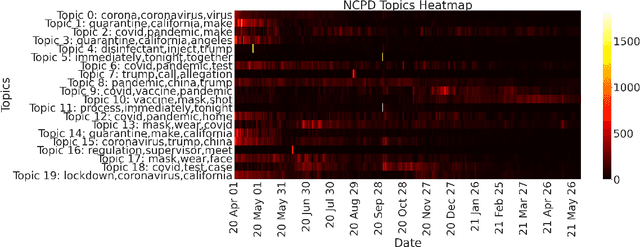
The construction and application of knowledge graphs have seen a rapid increase across many disciplines in recent years. Additionally, the problem of uncovering relationships between developments in the COVID-19 pandemic and social media behavior is of great interest to researchers hoping to curb the spread of the disease. In this paper we present a knowledge graph constructed from COVID-19 related tweets in the Los Angeles area, supplemented with federal and state policy announcements and disease spread statistics. By incorporating dates, topics, and events as entities, we construct a knowledge graph that describes the connections between these useful information. We use natural language processing and change point analysis to extract tweet-topic, tweet-date, and event-date relations. Further analysis on the constructed knowledge graph provides insight into how tweets reflect public sentiments towards COVID-19 related topics and how changes in these sentiments correlate with real-world events.

Heavy Ball Neural Ordinary Differential Equations

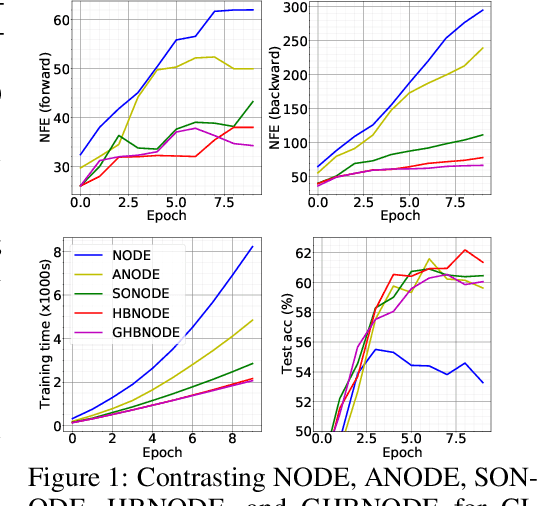
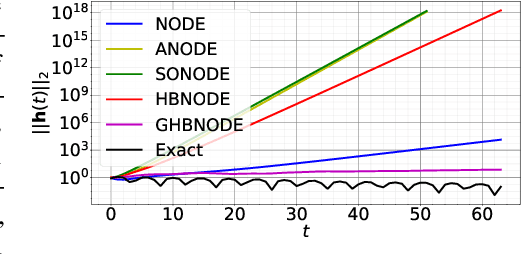
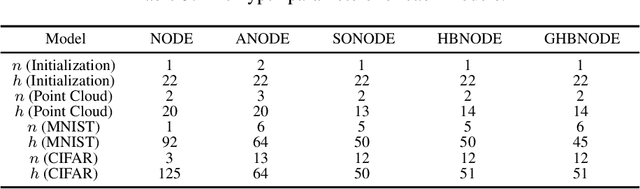
We propose heavy ball neural ordinary differential equations (HBNODEs), leveraging the continuous limit of the classical momentum accelerated gradient descent, to improve neural ODEs (NODEs) training and inference. HBNODEs have two properties that imply practical advantages over NODEs: (i) The adjoint state of an HBNODE also satisfies an HBNODE, accelerating both forward and backward ODE solvers, thus significantly reducing the number of function evaluations (NFEs) and improving the utility of the trained models. (ii) The spectrum of HBNODEs is well structured, enabling effective learning of long-term dependencies from complex sequential data. We verify the advantages of HBNODEs over NODEs on benchmark tasks, including image classification, learning complex dynamics, and sequential modeling. Our method requires remarkably fewer forward and backward NFEs, is more accurate, and learns long-term dependencies more effectively than the other ODE-based neural network models. Code is available at \url{https://github.com/hedixia/HeavyBallNODE}.

Post-Radiotherapy PET Image Outcome Prediction by Deep Learning under Biological Model Guidance: A Feasibility Study of Oropharyngeal Cancer Application

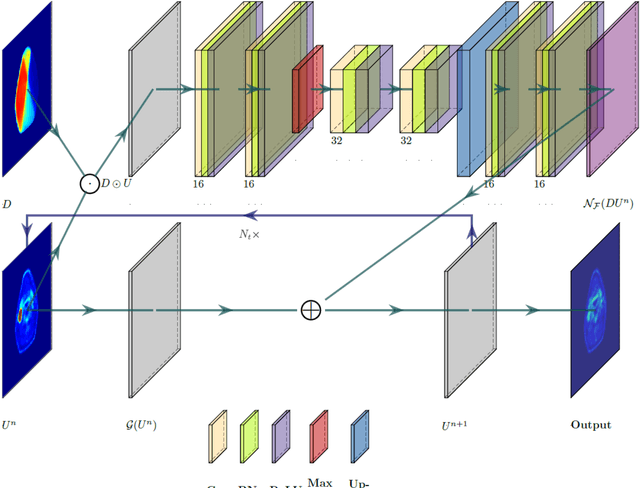
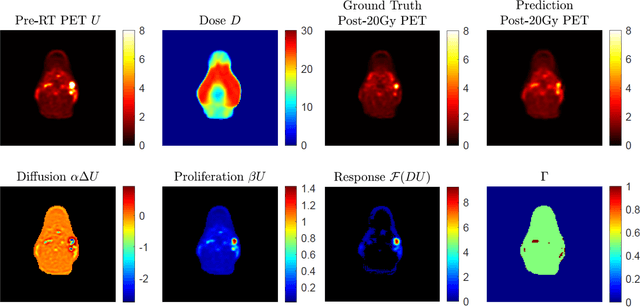
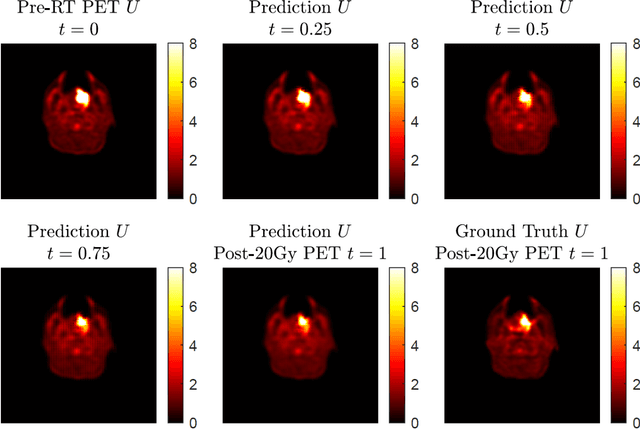
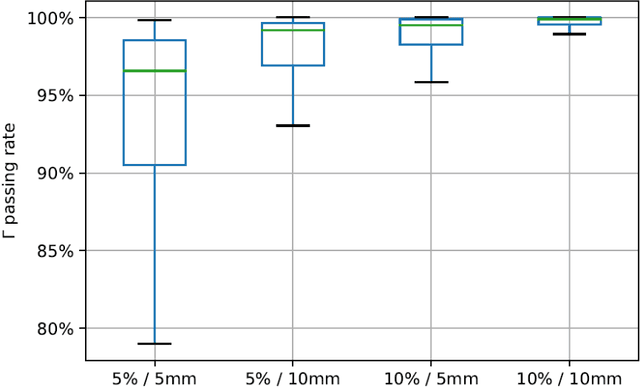
This paper develops a method of biologically guided deep learning for post-radiation FDG-PET image outcome prediction based on pre-radiation images and radiotherapy dose information. Based on the classic reaction-diffusion mechanism, a novel biological model was proposed using a partial differential equation that incorporates spatial radiation dose distribution as a patient-specific treatment information variable. A 7-layer encoder-decoder-based convolutional neural network (CNN) was designed and trained to learn the proposed biological model. As such, the model could generate post-radiation FDG-PET image outcome predictions with possible time-series transition from pre-radiotherapy image states to post-radiotherapy states. The proposed method was developed using 64 oropharyngeal patients with paired FDG-PET studies before and after 20Gy delivery (2Gy/daily fraction) by IMRT. In a two-branch deep learning execution, the proposed CNN learns specific terms in the biological model from paired FDG-PET images and spatial dose distribution as in one branch, and the biological model generates post-20Gy FDG-PET image prediction in the other branch. The proposed method successfully generated post-20Gy FDG-PET image outcome prediction with breakdown illustrations of biological model components. Time-series FDG-PET image predictions were generated to demonstrate the feasibility of disease response rendering. The developed biologically guided deep learning method achieved post-20Gy FDG-PET image outcome predictions in good agreement with ground-truth results. With break-down biological modeling components, the outcome image predictions could be used in adaptive radiotherapy decision-making to optimize personalized plans for the best outcome in the future.

Posterior Consistency of Semi-Supervised Regression on Graphs

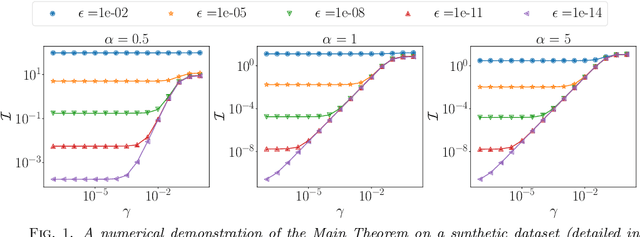
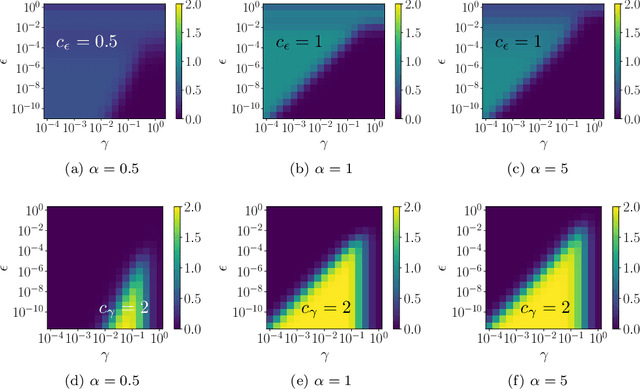
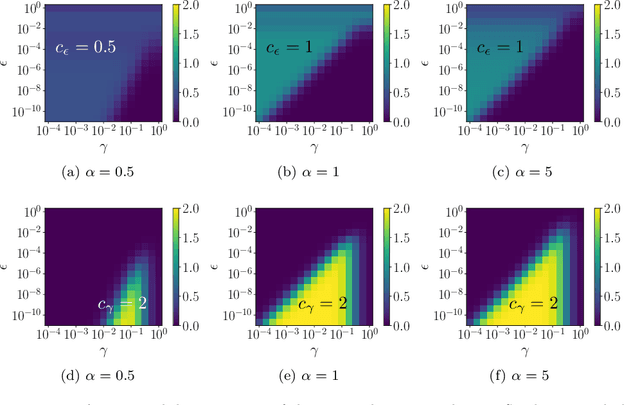
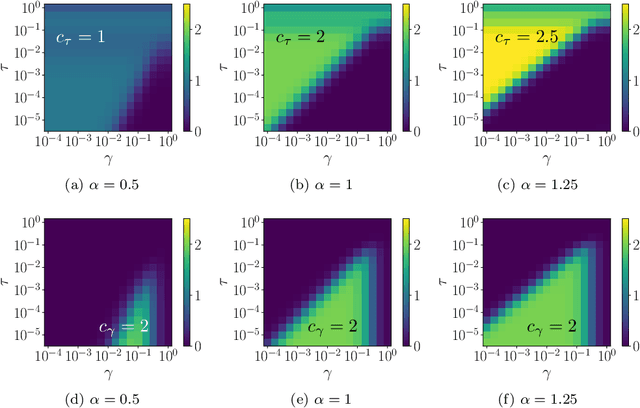
Graph-based semi-supervised regression (SSR) is the problem of estimating the value of a function on a weighted graph from its values (labels) on a small subset of the vertices. This paper is concerned with the consistency of SSR in the context of classification, in the setting where the labels have small noise and the underlying graph weighting is consistent with well-clustered nodes. We present a Bayesian formulation of SSR in which the weighted graph defines a Gaussian prior, using a graph Laplacian, and the labeled data defines a likelihood. We analyze the rate of contraction of the posterior measure around the ground truth in terms of parameters that quantify the small label error and inherent clustering in the graph. We obtain bounds on the rates of contraction and illustrate their sharpness through numerical experiments. The analysis also gives insight into the choice of hyperparameters that enter the definition of the prior.

Efficient Graph-Based Active Learning with Probit Likelihood via Gaussian Approximations

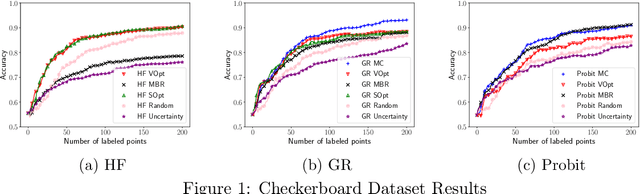
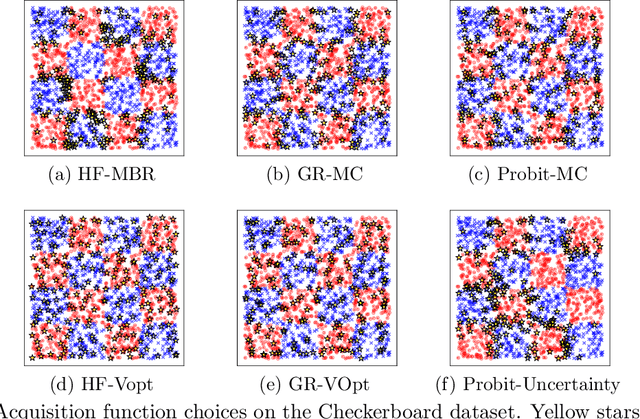
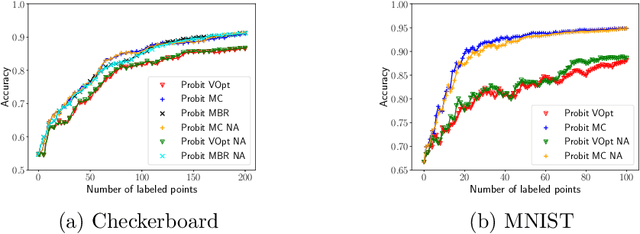
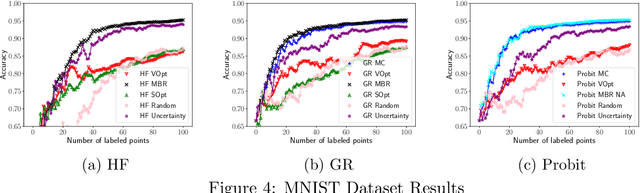
We present a novel adaptation of active learning to graph-based semi-supervised learning (SSL) under non-Gaussian Bayesian models. We present an approximation of non-Gaussian distributions to adapt previously Gaussian-based acquisition functions to these more general cases. We develop an efficient rank-one update for applying "look-ahead" based methods as well as model retraining. We also introduce a novel "model change" acquisition function based on these approximations that further expands the available collection of active learning acquisition functions for such methods.

MomentumRNN: Integrating Momentum into Recurrent Neural Networks

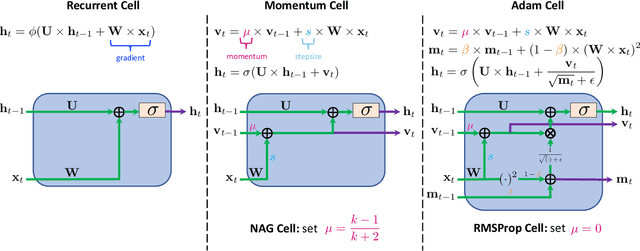
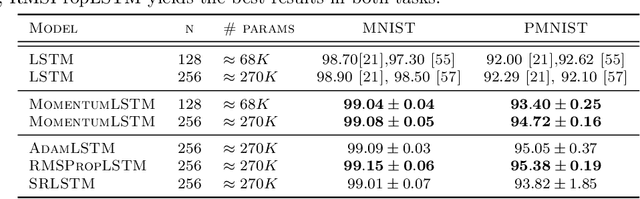
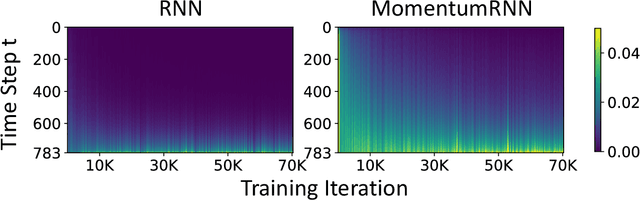
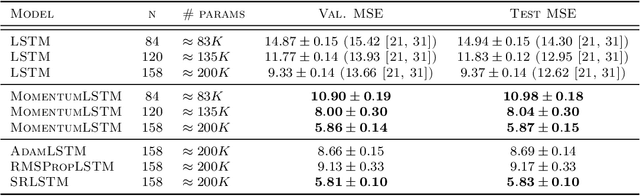
Designing deep neural networks is an art that often involves an expensive search over candidate architectures. To overcome this for recurrent neural nets (RNNs), we establish a connection between the hidden state dynamics in an RNN and gradient descent (GD). We then integrate momentum into this framework and propose a new family of RNNs, called {\em MomentumRNNs}. We theoretically prove and numerically demonstrate that MomentumRNNs alleviate the vanishing gradient issue in training RNNs. We study the momentum long-short term memory (MomentumLSTM) and verify its advantages in convergence speed and accuracy over its LSTM counterpart across a variety of benchmarks, with little compromise in computational or memory efficiency. We also demonstrate that MomentumRNN is applicable to many types of recurrent cells, including those in the state-of-the-art orthogonal RNNs. Finally, we show that other advanced momentum-based optimization methods, such as Adam and Nesterov accelerated gradients with a restart, can be easily incorporated into the MomentumRNN framework for designing new recurrent cells with even better performance. The code is available at \url{https://github.com/minhtannguyen/MomentumRNN}.