GLL: A Differentiable Graph Learning Layer for Neural Networks

Standard deep learning architectures used for classification generate label predictions with a projection head and softmax activation function. Although successful, these methods fail to leverage the relational information between samples in the batch for generating label predictions. In recent works, graph-based learning techniques, namely Laplace learning, have been heuristically combined with neural networks for both supervised and semi-supervised learning (SSL) tasks. However, prior works approximate the gradient of the loss function with respect to the graph learning algorithm or decouple the processes; end-to-end integration with neural networks is not achieved. In this work, we derive backpropagation equations, via the adjoint method, for inclusion of a general family of graph learning layers into a neural network. This allows us to precisely integrate graph Laplacian-based label propagation into a neural network layer, replacing a projection head and softmax activation function for classification tasks. Using this new framework, our experimental results demonstrate smooth label transitions across data, improved robustness to adversarial attacks, improved generalization, and improved training dynamics compared to the standard softmax-based approach.

Attraction-Repulsion Swarming: A Generalized Framework of t-SNE via Force Normalization and Tunable Interactions

We propose a new method for data visualization based on attraction-repulsion swarming (ARS) dynamics, which we call ARS visualization. ARS is a generalized framework that is based on viewing the t-distributed stochastic neighbor embedding (t-SNE) visualization technique as a swarm of interacting agents driven by attraction and repulsion. Motivated by recent developments in swarming, we modify the t-SNE dynamics to include a normalization by the \emph{total influence}, which results in better posed dynamics in which we can use a data size independent time step (of $h=1$) and a simple iteration, without the need for the array of optimization tricks employed in t-SNE. ARS also includes the ability to separately tune the attraction and repulsion kernels, which gives the user control over the tightness within clusters and the spacing between them in the visualization. In contrast with t-SNE, our proposed ARS data visualization method is not gradient descent on the Kullback-Leibler divergence, and can be viewed solely as an interacting particle system driven by attraction and repulsion forces. We provide theoretical results illustrating how the choice of interaction kernel affects the dynamics, and experimental results to validate our method and compare to t-SNE on the MNIST and Cifar-10 data sets.

En masse scanning and automated surfacing of small objects using Micro-CT

Modern archaeological methods increasingly utilize 3D virtual representations of objects, computationally intensive analyses, high resolution scanning, large datasets, and machine learning. With higher resolution scans, challenges surrounding computational power, memory, and file storage quickly arise. Processing and analyzing high resolution scans often requires memory-intensive workflows, which are infeasible for most computers and increasingly necessitate the use of super-computers or innovative methods for processing on standard computers. Here we introduce a novel protocol for en-masse micro-CT scanning of small objects with a {\em mostly-automated} processing workflow that functions in memory-limited settings. We scanned 1,112 animal bone fragments using just 10 micro-CT scans, which were post-processed into individual PLY files. Notably, our methods can be applied to any object (with discernible density from the packaging material) making this method applicable to a variety of inquiries and fields including paleontology, geology, electrical engineering, and materials science. Further, our methods may immediately be adopted by scanning institutes to pool customer orders together and offer more affordable scanning. The work presented herein is part of a larger program facilitated by the international and multi-disciplinary research consortium known as Anthropological and Mathematical Analysis of Archaeological and Zooarchaeological Evidence (AMAAZE). AMAAZE unites experts in anthropology, mathematics, and computer science to develop new methods for mass-scale virtual archaeological research. Overall, our new scanning method and processing workflows lay the groundwork and set the standard for future mass-scale, high resolution scanning studies.

Convergence rates for Poisson learning to a Poisson equation with measure data

In this paper we prove discrete to continuum convergence rates for Poisson Learning, a graph-based semi-supervised learning algorithm that is based on solving the graph Poisson equation with a source term consisting of a linear combination of Dirac deltas located at labeled points and carrying label information. The corresponding continuum equation is a Poisson equation with measure data in a Euclidean domain $\Omega \subset \mathbb{R}^d$. The singular nature of these equations is challenging and requires an approach with several distinct parts: (1) We prove quantitative error estimates when convolving the measure data of a Poisson equation with (approximately) radial function supported on balls. (2) We use quantitative variational techniques to prove discrete to continuum convergence rates on random geometric graphs with bandwidth $\varepsilon>0$ for bounded source terms. (3) We show how to regularize the graph Poisson equation via mollification with the graph heat kernel, and we study fine asymptotics of the heat kernel on random geometric graphs. Combining these three pillars we obtain $L^1$ convergence rates that scale, up to logarithmic factors, like $O(\varepsilon^{\frac{1}{d+2}})$ for general data distributions, and $O(\varepsilon^{\frac{2-\sigma}{d+4}})$ for uniformly distributed data, where $\sigma>0$. These rates are valid with high probability if $\varepsilon\gg\left({\log n}/{n}\right)^q$ where $n$ denotes the number of vertices of the graph and $q \approx \frac{1}{3d}$.

Numerical solution of a PDE arising from prediction with expert advice

This work investigates the online machine learning problem of prediction with expert advice in an adversarial setting through numerical analysis of, and experiments with, a related partial differential equation. The problem is a repeated two-person game involving decision-making at each step informed by $n$ experts in an adversarial environment. The continuum limit of this game over a large number of steps is a degenerate elliptic equation whose solution encodes the optimal strategies for both players. We develop numerical methods for approximating the solution of this equation in relatively high dimensions ($n\leq 10$) by exploiting symmetries in the equation and the solution to drastically reduce the size of the computational domain. Based on our numerical results we make a number of conjectures about the optimality of various adversarial strategies, in particular about the non-optimality of the COMB strategy.

Consistency of semi-supervised learning, stochastic tug-of-war games, and the p-Laplacian

In this paper we give a broad overview of the intersection of partial differential equations (PDEs) and graph-based semi-supervised learning. The overview is focused on a large body of recent work on PDE continuum limits of graph-based learning, which have been used to prove well-posedness of semi-supervised learning algorithms in the large data limit. We highlight some interesting research directions revolving around consistency of graph-based semi-supervised learning, and present some new results on the consistency of p-Laplacian semi-supervised learning using the stochastic tug-of-war game interpretation of the p-Laplacian. We also present the results of some numerical experiments that illustrate our results and suggest directions for future work.

Novel Batch Active Learning Approach and Its Application to Synthetic Aperture Radar Datasets

Active learning improves the performance of machine learning methods by judiciously selecting a limited number of unlabeled data points to query for labels, with the aim of maximally improving the underlying classifier's performance. Recent gains have been made using sequential active learning for synthetic aperture radar (SAR) data arXiv:2204.00005. In each iteration, sequential active learning selects a query set of size one while batch active learning selects a query set of multiple datapoints. While batch active learning methods exhibit greater efficiency, the challenge lies in maintaining model accuracy relative to sequential active learning methods. We developed a novel, two-part approach for batch active learning: Dijkstra's Annulus Core-Set (DAC) for core-set generation and LocalMax for batch sampling. The batch active learning process that combines DAC and LocalMax achieves nearly identical accuracy as sequential active learning but is more efficient, proportional to the batch size. As an application, a pipeline is built based on transfer learning feature embedding, graph learning, DAC, and LocalMax to classify the FUSAR-Ship and OpenSARShip datasets. Our pipeline outperforms the state-of-the-art CNN-based methods.

Poisson Reweighted Laplacian Uncertainty Sampling for Graph-based Active Learning

We show that uncertainty sampling is sufficient to achieve exploration versus exploitation in graph-based active learning, as long as the measure of uncertainty properly aligns with the underlying model and the model properly reflects uncertainty in unexplored regions. In particular, we use a recently developed algorithm, Poisson ReWeighted Laplace Learning (PWLL) for the classifier and we introduce an acquisition function designed to measure uncertainty in this graph-based classifier that identifies unexplored regions of the data. We introduce a diagonal perturbation in PWLL which produces exponential localization of solutions, and controls the exploration versus exploitation tradeoff in active learning. We use the well-posed continuum limit of PWLL to rigorously analyze our method, and present experimental results on a number of graph-based image classification problems.

Use and Misuse of Machine Learning in Anthropology

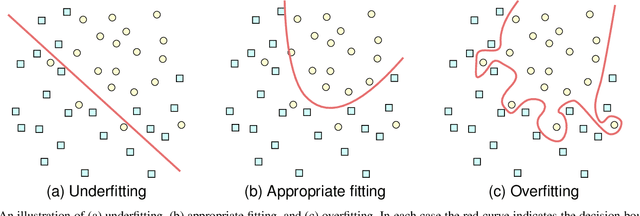
Machine learning (ML), being now widely accessible to the research community at large, has fostered a proliferation of new and striking applications of these emergent mathematical techniques across a wide range of disciplines. In this paper, we will focus on a particular case study: the field of paleoanthropology, which seeks to understand the evolution of the human species based on biological and cultural evidence. As we will show, the easy availability of ML algorithms and lack of expertise on their proper use among the anthropological research community has led to foundational misapplications that have appeared throughout the literature. The resulting unreliable results not only undermine efforts to legitimately incorporate ML into anthropological research, but produce potentially faulty understandings about our human evolutionary and behavioral past. The aim of this paper is to provide a brief introduction to some of the ways in which ML has been applied within paleoanthropology; we also include a survey of some basic ML algorithms for those who are not fully conversant with the field, which remains under active development. We discuss a series of missteps, errors, and violations of correct protocols of ML methods that appear disconcertingly often within the accumulating body of anthropological literature. These mistakes include use of outdated algorithms and practices; inappropriate train/test splits, sample composition, and textual explanations; as well as an absence of transparency due to the lack of data/code sharing, and the subsequent limitations imposed on independent replication. We assert that expanding samples, sharing data and code, re-evaluating approaches to peer review, and, most importantly, developing interdisciplinary teams that include experts in ML are all necessary for progress in future research incorporating ML within anthropology.

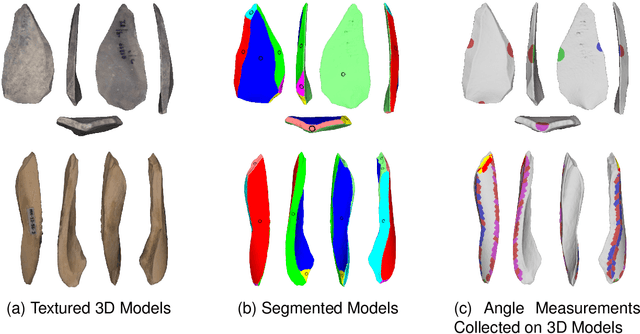
Using machine learning on new feature sets extracted from 3D models of broken animal bones to classify fragments according to break agent

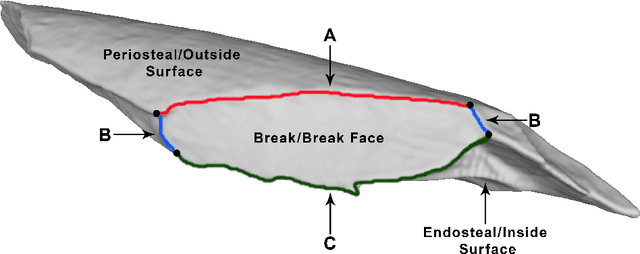
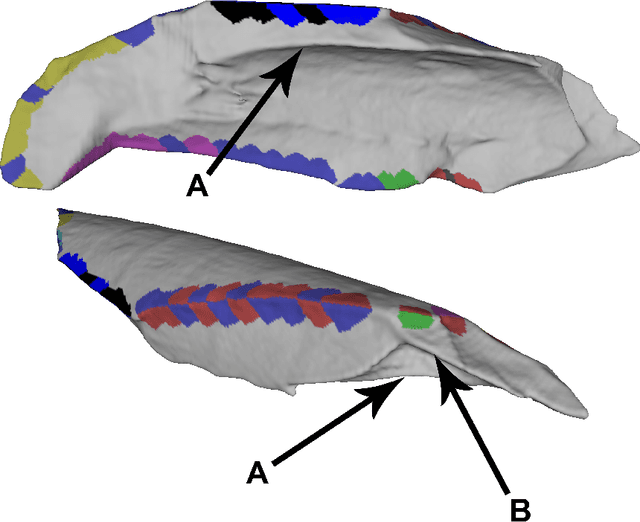
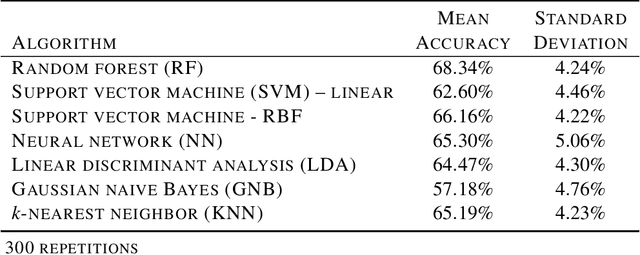
Distinguishing agents of bone modification at paleoanthropological sites is at the root of much of the research directed at understanding early hominin exploitation of large animal resources and the effects those subsistence behaviors had on early hominin evolution. However, current methods, particularly in the area of fracture pattern analysis as a signal of marrow exploitation, have failed to overcome equifinality. Furthermore, researchers debate the replicability and validity of current and emerging methods for analyzing bone modifications. Here we present a new approach to fracture pattern analysis aimed at distinguishing bone fragments resulting from hominin bone breakage and those produced by carnivores. This new method uses 3D models of fragmentary bone to extract a much richer dataset that is more transparent and replicable than feature sets previously used in fracture pattern analysis. Supervised machine learning algorithms are properly used to classify bone fragments according to agent of breakage with average mean accuracy of 77% across tests.