A Generalized Version of Chung's Lemma and its Applications

Chung's lemma is a classical tool for establishing asymptotic convergence rates of (stochastic) optimization methods under strong convexity-type assumptions and appropriate polynomial diminishing step sizes. In this work, we develop a generalized version of Chung's lemma, which provides a simple non-asymptotic convergence framework for a more general family of step size rules. We demonstrate broad applicability of the proposed generalized Chung's lemma by deriving tight non-asymptotic convergence rates for a large variety of stochastic methods. In particular, we obtain partially new non-asymptotic complexity results for stochastic optimization methods, such as stochastic gradient descent and random reshuffling, under a general $(\theta,\mu)$-Polyak-Lojasiewicz (PL) condition and for various step sizes strategies, including polynomial, constant, exponential, and cosine step sizes rules. Notably, as a by-product of our analysis, we observe that exponential step sizes can adapt to the objective function's geometry, achieving the optimal convergence rate without requiring exact knowledge of the underlying landscape. Our results demonstrate that the developed variant of Chung's lemma offers a versatile, systematic, and streamlined approach to establish non-asymptotic convergence rates under general step size rules.

A KL-based Analysis Framework with Applications to Non-Descent Optimization Methods

We propose a novel analysis framework for non-descent-type optimization methodologies in nonconvex scenarios based on the Kurdyka-Lojasiewicz property. Our framework allows covering a broad class of algorithms, including those commonly employed in stochastic and distributed optimization. Specifically, it enables the analysis of first-order methods that lack a sufficient descent property and do not require access to full (deterministic) gradient information. We leverage this framework to establish, for the first time, iterate convergence and the corresponding rates for the decentralized gradient method and federated averaging under mild assumptions. Furthermore, based on the new analysis techniques, we show the convergence of the random reshuffling and stochastic gradient descent method without necessitating typical a priori bounded iterates assumptions.

Convergence of SGD with momentum in the nonconvex case: A novel time window-based analysis

We propose a novel time window-based analysis technique to investigate the convergence behavior of the stochastic gradient descent method with momentum (SGDM) in nonconvex settings. Despite its popularity, the convergence behavior of SGDM remains less understood in nonconvex scenarios. This is primarily due to the absence of a sufficient descent property and challenges in controlling stochastic errors in an almost sure sense. To address these challenges, we study the behavior of SGDM over specific time windows, rather than examining the descent of consecutive iterates as in traditional analyses. This time window-based approach simplifies the convergence analysis and enables us to establish the first iterate convergence result for SGDM under the Kurdyka-Lojasiewicz (KL) property. Based on the underlying KL exponent and the utilized step size scheme, we further characterize local convergence rates of SGDM.

A New Random Reshuffling Method for Nonsmooth Nonconvex Finite-sum Optimization

In this work, we propose and study a novel stochastic optimization algorithm, termed the normal map-based proximal random reshuffling (norm-PRR) method, for nonsmooth nonconvex finite-sum problems. Random reshuffling techniques are prevalent and widely utilized in large-scale applications, e.g., in the training of neural networks. While the convergence behavior and advantageous acceleration effects of random reshuffling methods are fairly well understood in the smooth setting, much less seems to be known in the nonsmooth case and only few proximal-type random reshuffling approaches with provable guarantees exist. We establish the iteration complexity ${\cal O}(n^{-1/3}T^{-2/3})$ for norm-PRR, where $n$ is the number of component functions and $T$ counts the total number of iteration. We also provide novel asymptotic convergence results for norm-PRR. Specifically, under the Kurdyka-{\L}ojasiewicz (KL) inequality, we establish strong limit-point convergence, i.e., the iterates generated by norm-PRR converge to a single stationary point. Moreover, we derive last iterate convergence rates of the form ${\cal O}(k^{-p})$; here, $p \in [0, 1]$ depends on the KL exponent $\theta \in [0,1)$ and step size dynamics. Finally, we present preliminary numerical results on machine learning problems that demonstrate the efficiency of the proposed method.

Convergence of a Normal Map-based Prox-SGD Method under the KL Inequality

In this paper, we present a novel stochastic normal map-based algorithm ($\mathsf{norM}\text{-}\mathsf{SGD}$) for nonconvex composite-type optimization problems and discuss its convergence properties. Using a time window-based strategy, we first analyze the global convergence behavior of $\mathsf{norM}\text{-}\mathsf{SGD}$ and it is shown that every accumulation point of the generated sequence of iterates $\{\boldsymbol{x}^k\}_k$ corresponds to a stationary point almost surely and in an expectation sense. The obtained results hold under standard assumptions and extend the more limited convergence guarantees of the basic proximal stochastic gradient method. In addition, based on the well-known Kurdyka-{\L}ojasiewicz (KL) analysis framework, we provide novel point-wise convergence results for the iterates $\{\boldsymbol{x}^k\}_k$ and derive convergence rates that depend on the underlying KL exponent $\boldsymbol{\theta}$ and the step size dynamics $\{\alpha_k\}_k$. Specifically, for the popular step size scheme $\alpha_k=\mathcal{O}(1/k^\gamma)$, $\gamma \in (\frac23,1]$, (almost sure) rates of the form $\|\boldsymbol{x}^k-\boldsymbol{x}^*\| = \mathcal{O}(1/k^p)$, $p \in (0,\frac12)$, can be established. The obtained rates are faster than related and existing convergence rates for $\mathsf{SGD}$ and improve on the non-asymptotic complexity bounds for $\mathsf{norM}\text{-}\mathsf{SGD}$.

A Unified Convergence Theorem for Stochastic Optimization Methods

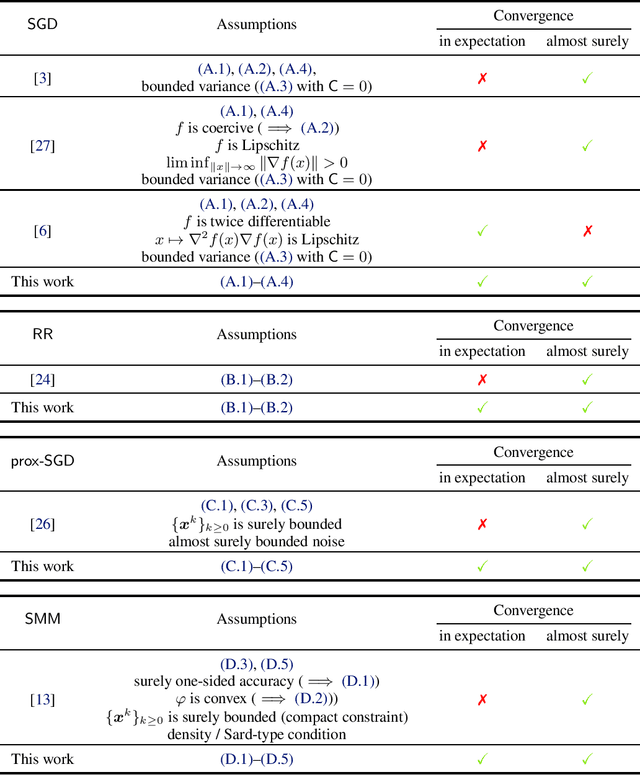
In this work, we provide a fundamental unified convergence theorem used for deriving expected and almost sure convergence results for a series of stochastic optimization methods. Our unified theorem only requires to verify several representative conditions and is not tailored to any specific algorithm. As a direct application, we recover expected and almost sure convergence results of the stochastic gradient method (SGD) and random reshuffling (RR) under more general settings. Moreover, we establish new expected and almost sure convergence results for the stochastic proximal gradient method (prox-SGD) and stochastic model-based methods (SMM) for nonsmooth nonconvex optimization problems. These applications reveal that our unified theorem provides a plugin-type convergence analysis and strong convergence guarantees for a wide class of stochastic optimization methods.

A Semismooth Newton Stochastic Proximal Point Algorithm with Variance Reduction

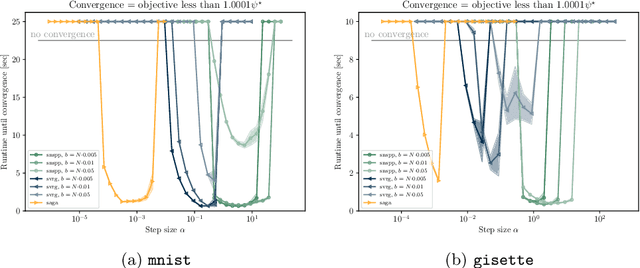
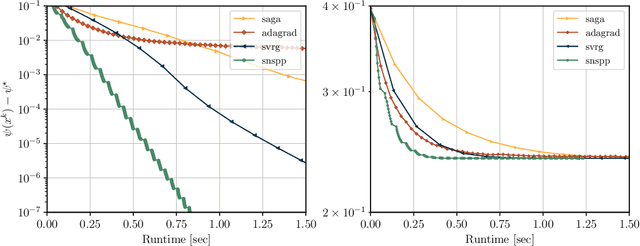
We develop an implementable stochastic proximal point (SPP) method for a class of weakly convex, composite optimization problems. The proposed stochastic proximal point algorithm incorporates a variance reduction mechanism and the resulting SPP updates are solved using an inexact semismooth Newton framework. We establish detailed convergence results that take the inexactness of the SPP steps into account and that are in accordance with existing convergence guarantees of (proximal) stochastic variance-reduced gradient methods. Numerical experiments show that the proposed algorithm competes favorably with other state-of-the-art methods and achieves higher robustness with respect to the step size selection.

Distributed Random Reshuffling over Networks

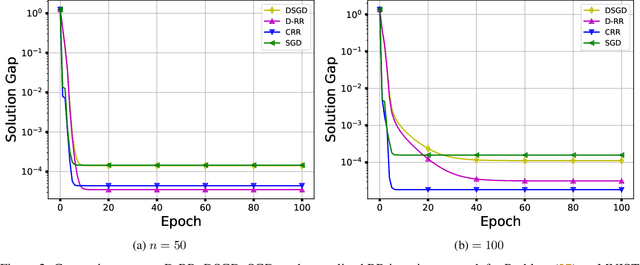
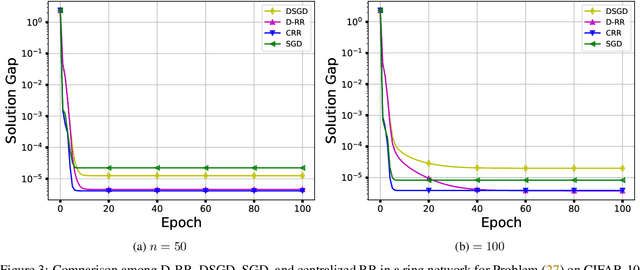
In this paper, we consider the distributed optimization problem where $n$ agents, each possessing a local cost function, collaboratively minimize the average of the local cost functions over a connected network. To solve the problem, we propose a distributed random reshuffling (D-RR) algorithm that combines the classical distributed gradient descent (DGD) method and Random Reshuffling (RR). We show that D-RR inherits the superiority of RR for both smooth strongly convex and smooth nonconvex objective functions. In particular, for smooth strongly convex objective functions, D-RR achieves $\mathcal{O}(1/T^2)$ rate of convergence (here, $T$ counts the total number of iterations) in terms of the squared distance between the iterate and the unique minimizer. When the objective function is assumed to be smooth nonconvex and has Lipschitz continuous component functions, we show that D-RR drives the squared norm of gradient to $0$ at a rate of $\mathcal{O}(1/T^{2/3})$. These convergence results match those of centralized RR (up to constant factors).

Convergence of Random Reshuffling Under The Kurdyka-Łojasiewicz Inequality

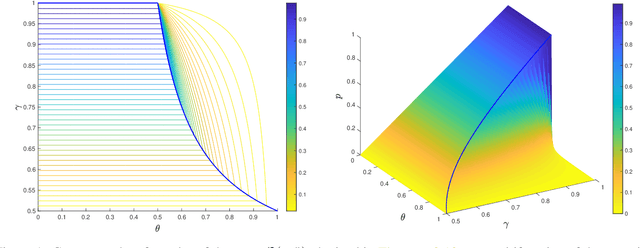
We study the random reshuffling (RR) method for smooth nonconvex optimization problems with a finite-sum structure. Though this method is widely utilized in practice such as the training of neural networks, its convergence behavior is only understood in several limited settings. In this paper, under the well-known Kurdyka-Lojasiewicz (KL) inequality, we establish strong limit-point convergence results for RR with appropriate diminishing step sizes, namely, the whole sequence of iterates generated by RR is convergent and converges to a single stationary point in an almost sure sense. In addition, we derive the corresponding rate of convergence, depending on the KL exponent and the suitably selected diminishing step sizes. When the KL exponent lies in $[0,\frac12]$, the convergence is at a rate of $\mathcal{O}(t^{-1})$ with $t$ counting the iteration number. When the KL exponent belongs to $(\frac12,1)$, our derived convergence rate is of the form $\mathcal{O}(t^{-q})$ with $q\in (0,1)$ depending on the KL exponent. The standard KL inequality-based convergence analysis framework only applies to algorithms with a certain descent property. Remarkably, we conduct convergence analysis for the non-descent RR with diminishing step sizes based on the KL inequality, which generalizes the standard KL analysis framework. We summarize our main steps and core ideas in an analysis framework, which is of independent interest. As a direct application of this framework, we also establish similar strong limit-point convergence results for the shuffled proximal point method.

A Stochastic Extra-Step Quasi-Newton Method for Nonsmooth Nonconvex Optimization

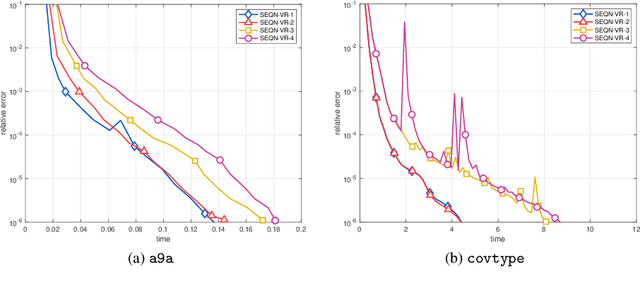
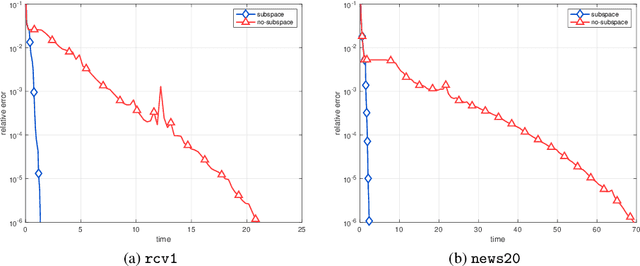
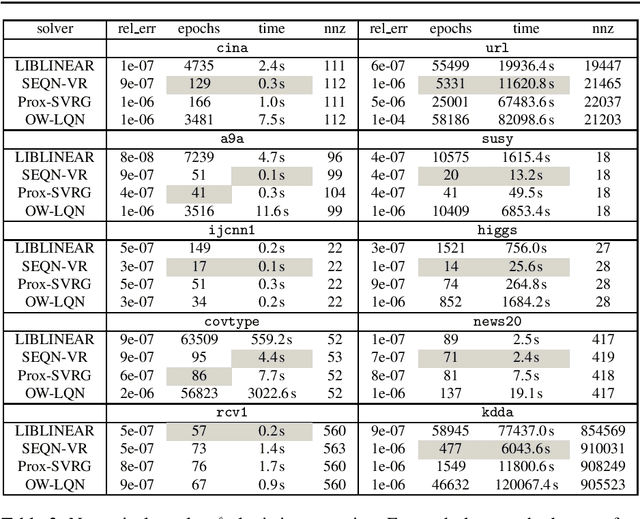
In this paper, a novel stochastic extra-step quasi-Newton method is developed to solve a class of nonsmooth nonconvex composite optimization problems. We assume that the gradient of the smooth part of the objective function can only be approximated by stochastic oracles. The proposed method combines general stochastic higher order steps derived from an underlying proximal type fixed-point equation with additional stochastic proximal gradient steps to guarantee convergence. Based on suitable bounds on the step sizes, we establish global convergence to stationary points in expectation and an extension of the approach using variance reduction techniques is discussed. Motivated by large-scale and big data applications, we investigate a stochastic coordinate-type quasi-Newton scheme that allows to generate cheap and tractable stochastic higher order directions. Finally, the proposed algorithm is tested on large-scale logistic regression and deep learning problems and it is shown that it compares favorably with other state-of-the-art methods.