SGD with Clipping is Secretly Estimating the Median Gradient

There are several applications of stochastic optimization where one can benefit from a robust estimate of the gradient. For example, domains such as distributed learning with corrupted nodes, the presence of large outliers in the training data, learning under privacy constraints, or even heavy-tailed noise due to the dynamics of the algorithm itself. Here we study SGD with robust gradient estimators based on estimating the median. We first consider computing the median gradient across samples, and show that the resulting method can converge even under heavy-tailed, state-dependent noise. We then derive iterative methods based on the stochastic proximal point method for computing the geometric median and generalizations thereof. Finally we propose an algorithm estimating the median gradient across iterations, and find that several well known methods - in particular different forms of clipping - are particular cases of this framework.

Function Value Learning: Adaptive Learning Rates Based on the Polyak Stepsize and Function Splitting in ERM

Here we develop variants of SGD (stochastic gradient descent) with an adaptive step size that make use of the sampled loss values. In particular, we focus on solving a finite sum-of-terms problem, also known as empirical risk minimization. We first detail an idealized adaptive method called $\texttt{SPS}_+$ that makes use of the sampled loss values and assumes knowledge of the sampled loss at optimality. This $\texttt{SPS}_+$ is a minor modification of the SPS (Stochastic Polyak Stepsize) method, where the step size is enforced to be positive. We then show that $\texttt{SPS}_+$ achieves the best known rates of convergence for SGD in the Lipschitz non-smooth. We then move onto to develop $\texttt{FUVAL}$, a variant of $\texttt{SPS}_+$ where the loss values at optimality are gradually learned, as opposed to being given. We give three viewpoints of $\texttt{FUVAL}$, as a projection based method, as a variant of the prox-linear method, and then as a particular online SGD method. We then present a convergence analysis of $\texttt{FUVAL}$ and experimental results. The shortcomings of our work is that the convergence analysis of $\texttt{FUVAL}$ shows no advantage over SGD. Another shortcomming is that currently only the full batch version of $\texttt{FUVAL}$ shows a minor advantages of GD (Gradient Descent) in terms of sensitivity to the step size. The stochastic version shows no clear advantage over SGD. We conjecture that large mini-batches are required to make $\texttt{FUVAL}$ competitive. Currently the new $\texttt{FUVAL}$ method studied in this paper does not offer any clear theoretical or practical advantage. We have chosen to make this draft available online nonetheless because of some of the analysis techniques we use, such as the non-smooth analysis of $\texttt{SPS}_+$, and also to show an apparently interesting approach that currently does not work.

MoMo: Momentum Models for Adaptive Learning Rates

We present new adaptive learning rates that can be used with any momentum method. To showcase our new learning rates we develop MoMo and MoMo-Adam, which are SGD with momentum (SGDM) and Adam together with our new adaptive learning rates. Our MoMo methods are motivated through model-based stochastic optimization, wherein we use momentum estimates of the batch losses and gradients sampled at each iteration to build a model of the loss function. Our model also makes use of any known lower bound of the loss function by using truncation. Indeed most losses are bounded below by zero. We then approximately minimize this model at each iteration to compute the next step. For losses with unknown lower bounds, we develop new on-the-fly estimates of the lower bound that we use in our model. Numerical experiments show that our MoMo methods improve over SGDM and Adam in terms of accuracy and robustness to hyperparameter tuning for training image classifiers on MNIST, CIFAR10, CIFAR100, Imagenet32, DLRM on the Criteo dataset, and a transformer model on the translation task IWSLT14.

A Stochastic Proximal Polyak Step Size

Recently, the stochastic Polyak step size (SPS) has emerged as a competitive adaptive step size scheme for stochastic gradient descent. Here we develop ProxSPS, a proximal variant of SPS that can handle regularization terms. Developing a proximal variant of SPS is particularly important, since SPS requires a lower bound of the objective function to work well. When the objective function is the sum of a loss and a regularizer, available estimates of a lower bound of the sum can be loose. In contrast, ProxSPS only requires a lower bound for the loss which is often readily available. As a consequence, we show that ProxSPS is easier to tune and more stable in the presence of regularization. Furthermore for image classification tasks, ProxSPS performs as well as AdamW with little to no tuning, and results in a network with smaller weight parameters. We also provide an extensive convergence analysis for ProxSPS that includes the non-smooth, smooth, weakly convex and strongly convex setting.

A Semismooth Newton Stochastic Proximal Point Algorithm with Variance Reduction

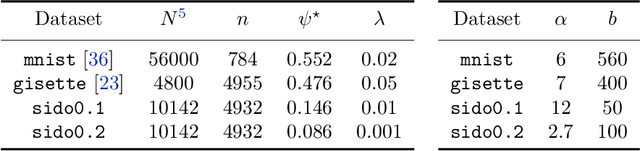
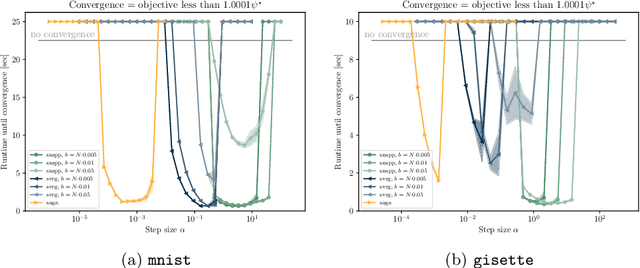
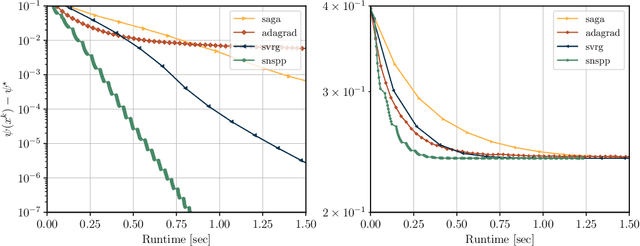
We develop an implementable stochastic proximal point (SPP) method for a class of weakly convex, composite optimization problems. The proposed stochastic proximal point algorithm incorporates a variance reduction mechanism and the resulting SPP updates are solved using an inexact semismooth Newton framework. We establish detailed convergence results that take the inexactness of the SPP steps into account and that are in accordance with existing convergence guarantees of (proximal) stochastic variance-reduced gradient methods. Numerical experiments show that the proposed algorithm competes favorably with other state-of-the-art methods and achieves higher robustness with respect to the step size selection.