Online Convex Optimization and Integral Quadratic Constraints: A new approach to regret analysis

We propose a novel approach for analyzing dynamic regret of first-order constrained online convex optimization algorithms for strongly convex and Lipschitz-smooth objectives. Crucially, we provide a general analysis that is applicable to a wide range of first-order algorithms that can be expressed as an interconnection of a linear dynamical system in feedback with a first-order oracle. By leveraging Integral Quadratic Constraints (IQCs), we derive a semi-definite program which, when feasible, provides a regret guarantee for the online algorithm. For this, the concept of variational IQCs is introduced as the generalization of IQCs to time-varying monotone operators. Our bounds capture the temporal rate of change of the problem in the form of the path length of the time-varying minimizer and the objective function variation. In contrast to standard results in OCO, our results do not require nerither the assumption of gradient boundedness, nor that of a bounded feasible set. Numerical analyses showcase the ability of the approach to capture the dependence of the regret on the function class condition number.

End-to-end guarantees for indirect data-driven control of bilinear systems with finite stochastic data

In this paper we propose an end-to-end algorithm for indirect data-driven control for bilinear systems with stability guarantees. We consider the case where the collected i.i.d. data is affected by probabilistic noise with possibly unbounded support and leverage tools from statistical learning theory to derive finite sample identification error bounds. To this end, we solve the bilinear identification problem by solving a set of linear and affine identification problems, by a particular choice of a control input during the data collection phase. We provide a priori as well as data-dependent finite sample identification error bounds on the individual matrices as well as ellipsoidal bounds, both of which are structurally suitable for control. Further, we integrate the structure of the derived identification error bounds in a robust controller design to obtain an exponentially stable closed-loop. By means of an extensive numerical study we showcase the interplay between the controller design and the derived identification error bounds. Moreover, we note appealing connections of our results to indirect data-driven control of general nonlinear systems through Koopman operator theory and discuss how our results may be applied in this setup.

Sample Complexity Bounds for Linear System Identification from a Finite Set

This paper considers a finite sample perspective on the problem of identifying an LTI system from a finite set of possible systems using trajectory data. To this end, we use the maximum likelihood estimator to identify the true system and provide an upper bound for its sample complexity. Crucially, the derived bound does not rely on a potentially restrictive stability assumption. Additionally, we leverage tools from information theory to provide a lower bound to the sample complexity that holds independently of the used estimator. The derived sample complexity bounds are analyzed analytically and numerically.

Implications of Regret on Stability of Linear Dynamical Systems

The setting of an agent making decisions under uncertainty and under dynamic constraints is common for the fields of optimal control, reinforcement learning and recently also for online learning. In the online learning setting, the quality of an agent's decision is often quantified by the concept of regret, comparing the performance of the chosen decisions to the best possible ones in hindsight. While regret is a useful performance measure, when dynamical systems are concerned, it is important to also assess the stability of the closed-loop system for a chosen policy. In this work, we show that for linear state feedback policies and linear systems subject to adversarial disturbances, linear regret implies asymptotic stability in both time-varying and time-invariant settings. Conversely, we also show that bounded input bounded state (BIBS) stability and summability of the state transition matrices imply linear regret.

Regret Analysis of Online Gradient Descent-based Iterative Learning Control with Model Mismatch

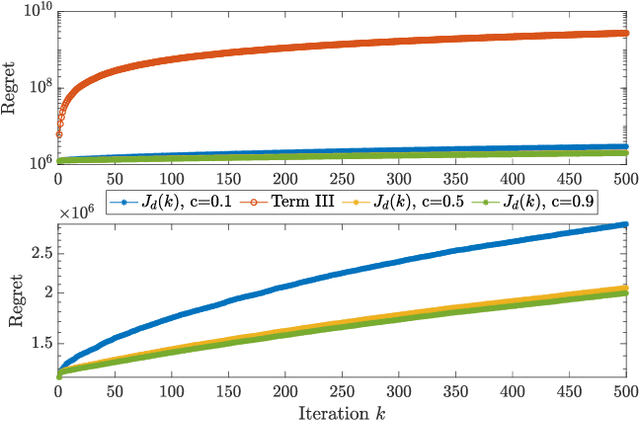
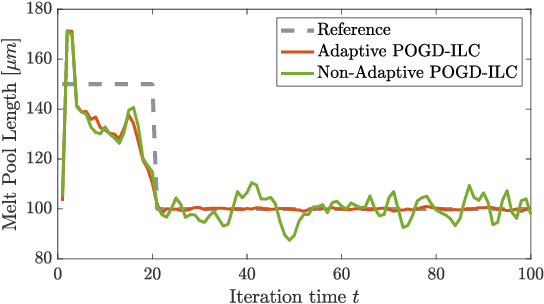
In Iterative Learning Control (ILC), a sequence of feedforward control actions is generated at each iteration on the basis of partial model knowledge and past measurements with the goal of steering the system toward a desired reference trajectory. This is framed here as an online learning task, where the decision-maker takes sequential decisions by solving a sequence of optimization problems having only partial knowledge of the cost functions. Having established this connection, the performance of an online gradient-descent based scheme using inexact gradient information is analyzed in the setting of dynamic and static regret, standard measures in online learning. Fundamental limitations of the scheme and its integration with adaptation mechanisms are further investigated, followed by numerical simulations on a benchmark ILC problem.

Infinite-Dimensional Sparse Learning in Linear System Identification

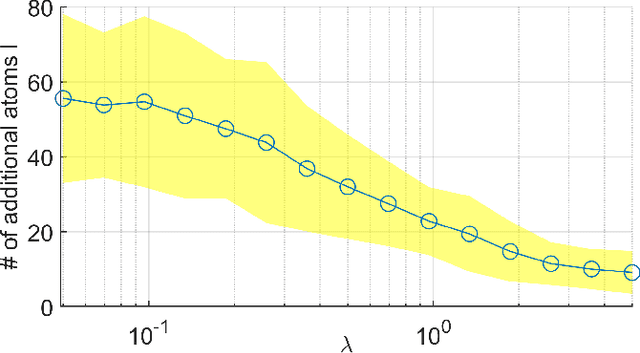
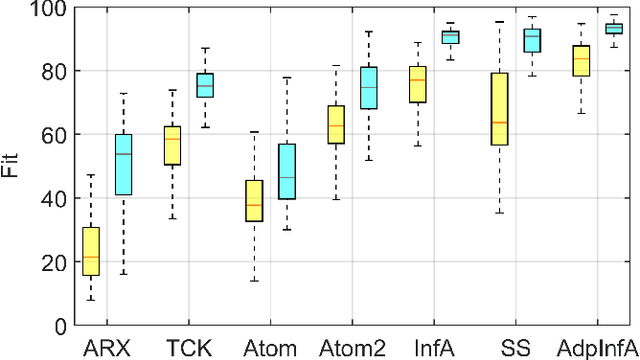
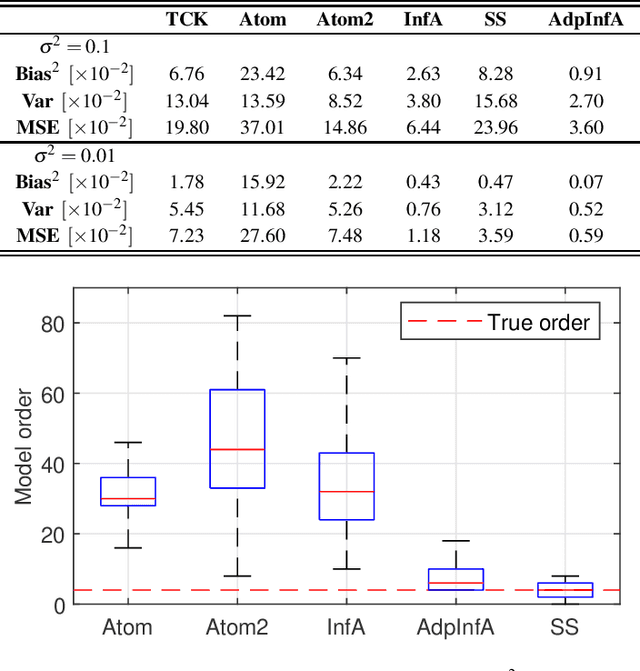
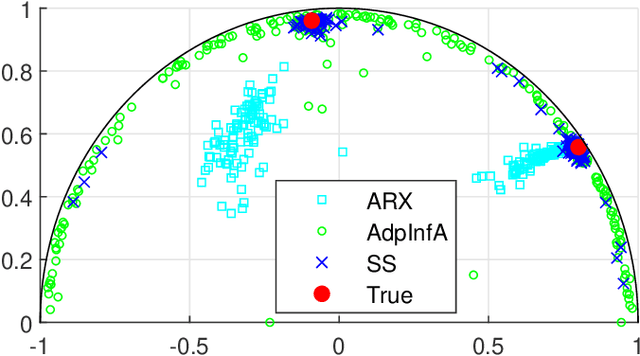
Regularized methods have been widely applied to system identification problems without known model structures. This paper proposes an infinite-dimensional sparse learning algorithm based on atomic norm regularization. Atomic norm regularization decomposes the transfer function into first-order atomic models and solves a group lasso problem that selects a sparse set of poles and identifies the corresponding coefficients. The difficulty in solving the problem lies in the fact that there are an infinite number of possible atomic models. This work proposes a greedy algorithm that generates new candidate atomic models maximizing the violation of the optimality condition of the existing problem. This algorithm is able to solve the infinite-dimensional group lasso problem with high precision. The algorithm is further extended to reduce the bias and reject false positives in pole location estimation by iteratively reweighted adaptive group lasso and complementary pairs stability selection respectively. Numerical results demonstrate that the proposed algorithm performs better than benchmark parameterized and regularized methods in terms of both impulse response fitting and pole location estimation.

Learning Dynamical Systems using Local Stability Priors

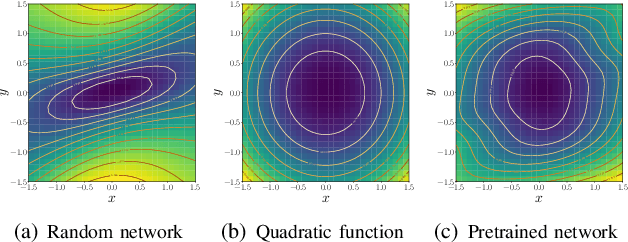
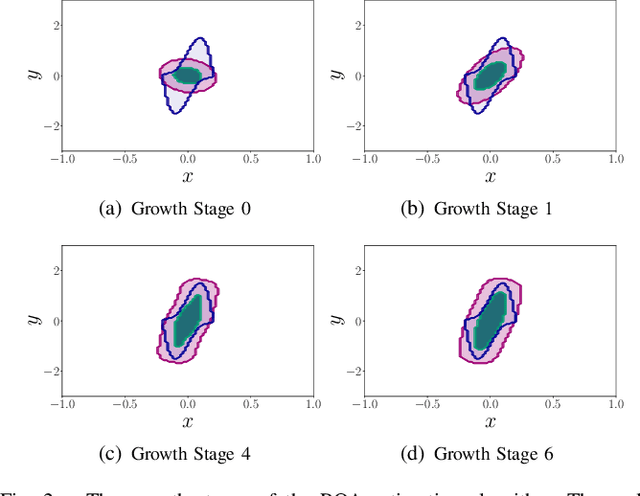
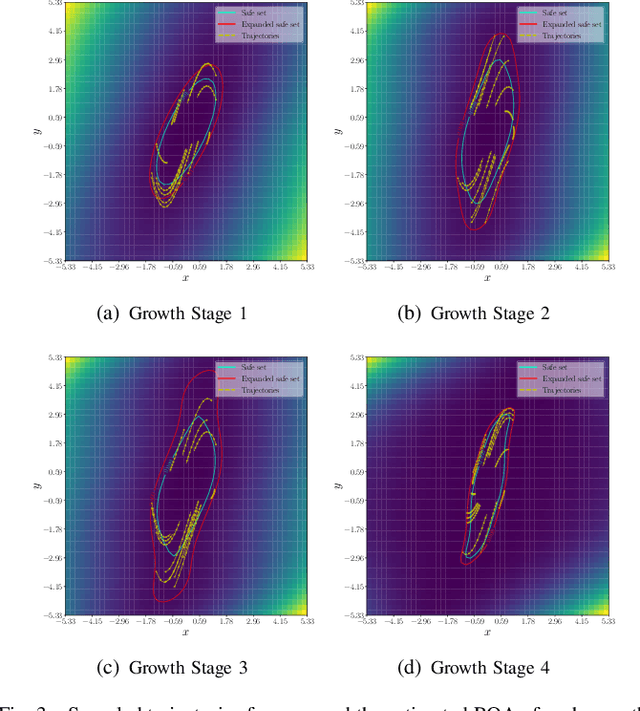
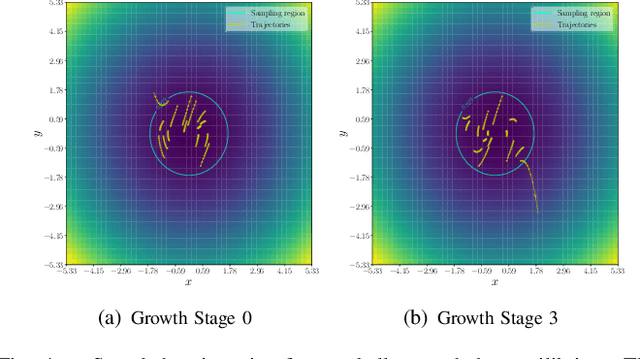
A coupled computational approach to simultaneously learn a vector field and the region of attraction of an equilibrium point from generated trajectories of the system is proposed. The nonlinear identification leverages the local stability information as a prior on the system, effectively endowing the estimate with this important structural property. In addition, the knowledge of the region of attraction plays an experiment design role by informing the selection of initial conditions from which trajectories are generated and by enabling the use of a Lyapunov function of the system as a regularization term. Numerical results show that the proposed method allows efficient sampling and provides an accurate estimate of the dynamics in an inner approximation of its region of attraction.