Electrical Fault Localisation Over a Distributed Parameter Transmission Line

Motivated by the need to localise faults along electrical power lines, this paper adopts a frequency-domain approach to parameter estimation for an infinite-dimensional linear dynamical system with one spatial variable. Since the time of the fault is unknown, and voltages and currents are measured at only one end of the line, distance information must be extracted from the post-fault transients. To properly account for high-frequency transient behaviour, the line dynamics is modelled directly by the Telegrapher's equation, rather than the more commonly used lumped-parameter approximations. First, the governing equations are non-dimensionalised to avoid ill-conditioning. A closed-form expression for the transfer function is then derived. Finally, nonlinear least-squares optimisation is employed to search for the fault location. Requirements on fault bandwidth, sensor bandwidth and simulation time-step are also presented. The result is a novel end-to-end algorithm for data generation and fault localisation, the effectiveness of which is demonstrated via simulation.

How are policy gradient methods affected by the limits of control?

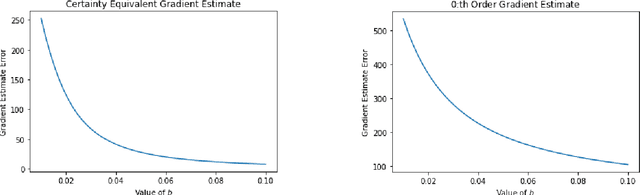
We study stochastic policy gradient methods from the perspective of control-theoretic limitations. Our main result is that ill-conditioned linear systems in the sense of Doyle inevitably lead to noisy gradient estimates. We also give an example of a class of stable systems in which policy gradient methods suffer from the curse of dimensionality. Our results apply to both state feedback and partially observed systems.

Single Trajectory Nonparametric Learning of Nonlinear Dynamics

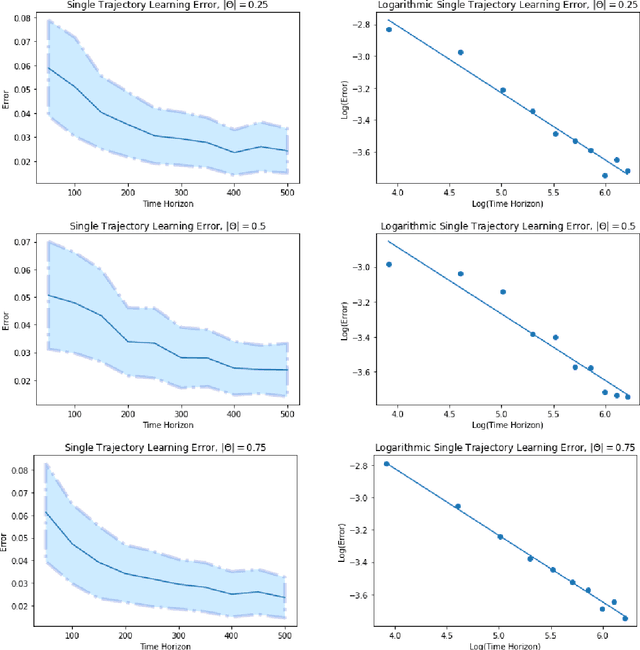
Given a single trajectory of a dynamical system, we analyze the performance of the nonparametric least squares estimator (LSE). More precisely, we give nonasymptotic expected $l^2$-distance bounds between the LSE and the true regression function, where expectation is evaluated on a fresh, counterfactual, trajectory. We leverage recently developed information-theoretic methods to establish the optimality of the LSE for nonparametric hypotheses classes in terms of supremum norm metric entropy and a subgaussian parameter. Next, we relate this subgaussian parameter to the stability of the underlying process using notions from dynamical systems theory. When combined, these developments lead to rate-optimal error bounds that scale as $T^{-1/(2+q)}$ for suitably stable processes and hypothesis classes with metric entropy growth of order $\delta^{-q}$. Here, $T$ is the length of the observed trajectory, $\delta \in \mathbb{R}_+$ is the packing granularity and $q\in (0,2)$ is a complexity term. Finally, we specialize our results to a number of scenarios of practical interest, such as Lipschitz dynamics, generalized linear models, and dynamics described by functions in certain classes of Reproducing Kernel Hilbert Spaces (RKHS).

Regret Lower Bounds for Learning Linear Quadratic Gaussian Systems

This paper presents local minimax regret lower bounds for adaptively controlling linear-quadratic-Gaussian (LQG) systems. We consider smoothly parametrized instances and provide an understanding of when logarithmic regret is impossible which is both instance specific and flexible enough to take problem structure into account. This understanding relies on two key notions: That of local-uninformativeness; when the optimal policy does not provide sufficient excitation for identification of the optimal policy, and yields a degenerate Fisher information matrix; and that of information-regret-boundedness, when the small eigenvalues of a policy-dependent information matrix are boundable in terms of the regret of that policy. Combined with a reduction to Bayesian estimation and application of Van Trees' inequality, these two conditions are sufficient for proving regret bounds on order of magnitude $\sqrt{T}$ in the time horizon, $T$. This method yields lower bounds that exhibit tight dimensional dependencies and scale naturally with control-theoretic problem constants. For instance, we are able to prove that systems operating near marginal stability are fundamentally hard to learn to control. We further show that large classes of systems satisfy these conditions, among them any state-feedback system with both $A$- and $B$-matrices unknown. Most importantly, we also establish that a nontrivial class of partially observable systems, essentially those that are over-actuated, satisfy these conditions, thus providing a $\sqrt{T}$ lower bound also valid for partially observable systems. Finally, we turn to two simple examples which demonstrate that our lower bound captures classical control-theoretic intuition: our lower bounds diverge for systems operating near marginal stability or with large filter gain -- these can be arbitrarily hard to (learn to) control.

On Uninformative Optimal Policies in Adaptive LQR with Unknown B-Matrix

This paper presents local asymptotic minimax regret lower bounds for adaptive Linear Quadratic Regulators (LQR). We consider affinely parametrized $B$-matrices and known $A$-matrices and aim to understand when logarithmic regret is impossible even in the presence of structural side information. After defining the intrinsic notion of an uninformative optimal policy in terms of a singularity condition for Fisher information we obtain local minimax regret lower bounds for such uninformative instances of LQR by appealing to van Trees' inequality (Bayesian Cram\'er-Rao) and a representation of regret in terms of a quadratic form (Bellman error). It is shown that if the parametrization induces an uninformative optimal policy, logarithmic regret is impossible and the rate is at least order square root in the time horizon. We explicitly characterize the notion of an uninformative optimal policy in terms of the nullspaces of system-theoretic quantities and the particular instance parametrization.

Privacy Preserving Set-Based Estimation Using Partially Homomorphic Encryption

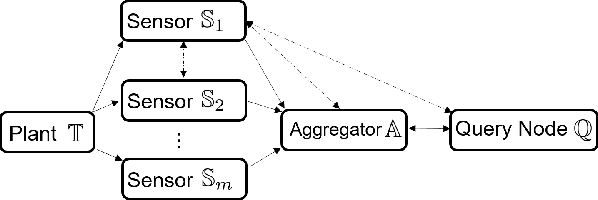
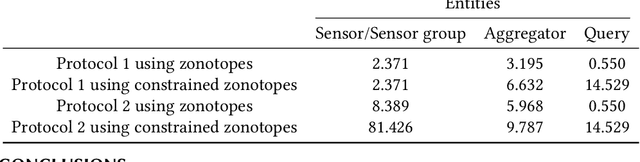
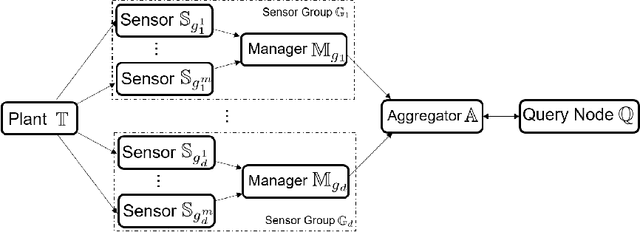
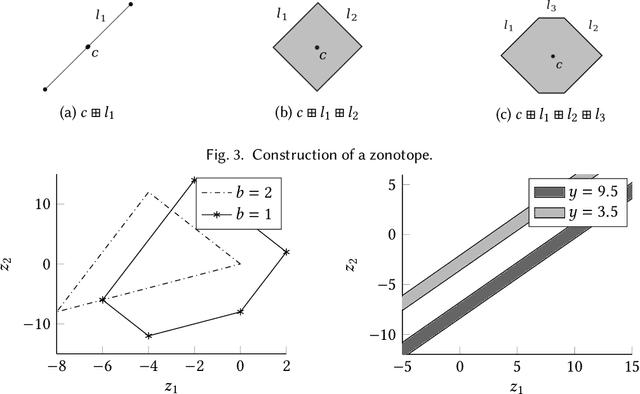
Set-based estimation has gained a lot of attention due to its ability to guarantee state enclosures for safety-critical systems. However, it requires computationally expensive operations, which in turn often requires outsourcing of these operations to cloud-computing platforms. Consequently, this raises some concerns with regard to sharing sensitive information and measurements. This paper presents the first privacy-preserving set-based estimation protocols using partially homomorphic encryption in which we preserve the privacy of the set of all possible estimates and the measurements. We consider a linear discrete-time dynamical system with bounded modeling and measurement uncertainties without any other statistical assumptions. We represent sets by zonotopes and constrained zonotopes as they can compactly represent high-dimensional sets and are closed under linear maps and Minkowski addition. By selectively encrypting some parameters of the used set representations, we are able to intersect sets in the encrypted domain, which enables guaranteed state estimation while ensuring the privacy goals. In particular, we show that our protocols achieve computational privacy using formal cryptographic definitions of computational indistinguishability. We demonstrate the efficiency of our approach by localizing a mobile quadcopter using custom ultra-wideband wireless devices. Our code and data are available online.

Two-Way Coding and Attack Decoupling in Control Systems Under Injection Attacks

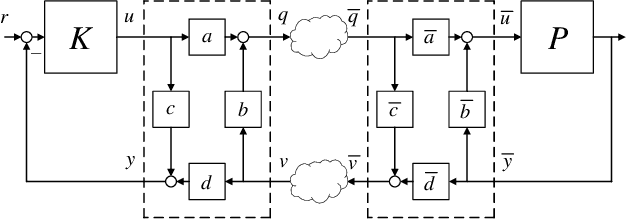
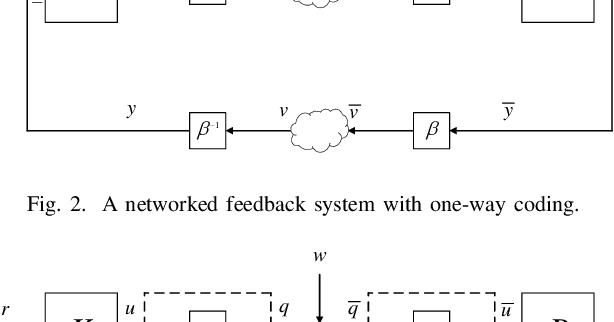
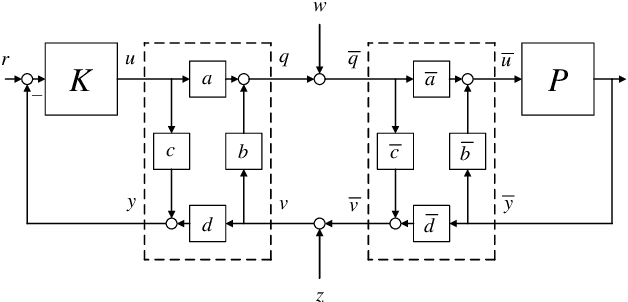
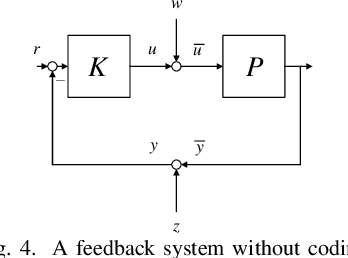
In this paper, we introduce the concept of two-way coding, which originates in communication theory characterizing coding schemes for two-way channels, into control theory, particularly to facilitate the analysis and design of feedback control systems under injection attacks. Moreover, we propose the notion of attack decoupling, and show how the controller and the two-way coding can be co-designed to nullify the transfer function from attack to plant, rendering the attack effect zero both in transient phase and in steady state.