Finite Sample Frequency Domain Identification

We study non-parametric frequency-domain system identification from a finite-sample perspective. We assume an open loop scenario where the excitation input is periodic and consider the Empirical Transfer Function Estimate (ETFE), where the goal is to estimate the frequency response at certain desired (evenly-spaced) frequencies, given input-output samples. We show that under sub-Gaussian colored noise (in time-domain) and stability assumptions, the ETFE estimates are concentrated around the true values. The error rate is of the order of $\mathcal{O}((d_{\mathrm{u}}+\sqrt{d_{\mathrm{u}}d_{\mathrm{y}}})\sqrt{M/N_{\mathrm{tot}}})$, where $N_{\mathrm{tot}}$ is the total number of samples, $M$ is the number of desired frequencies, and $d_{\mathrm{u}},\,d_{\mathrm{y}}$ are the dimensions of the input and output signals respectively. This rate remains valid for general irrational transfer functions and does not require a finite order state-space representation. By tuning $M$, we obtain a $N_{\mathrm{tot}}^{-1/3}$ finite-sample rate for learning the frequency response over all frequencies in the $ \mathcal{H}_{\infty}$ norm. Our result draws upon an extension of the Hanson-Wright inequality to semi-infinite matrices. We study the finite-sample behavior of ETFE in simulations.

Online Identification of Stochastic Continuous-Time Wiener Models Using Sampled Data

It is well known that ignoring the presence of stochastic disturbances in the identification of stochastic Wiener models leads to asymptotically biased estimators. On the other hand, optimal statistical identification, via likelihood-based methods, is sensitive to the assumptions on the data distribution and is usually based on relatively complex sequential Monte Carlo algorithms. We develop a simple recursive online estimation algorithm based on an output-error predictor, for the identification of continuous-time stochastic parametric Wiener models through stochastic approximation. The method is applicable to generic model parameterizations and, as demonstrated in the numerical simulation examples, it is robust with respect to the assumptions on the spectrum of the disturbance process.

Continuous Time-Delay Estimation From Sampled Measurements

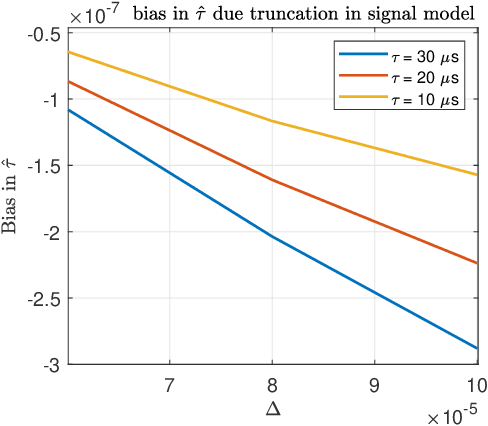
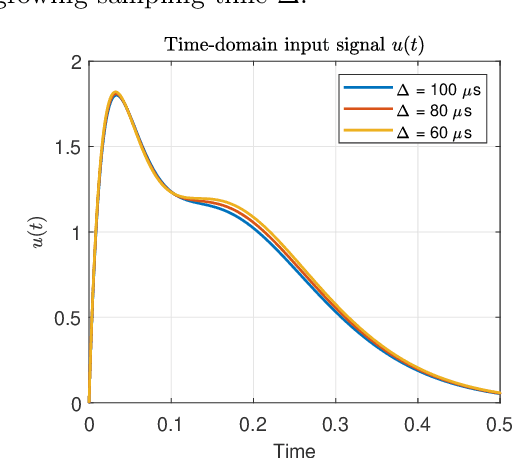
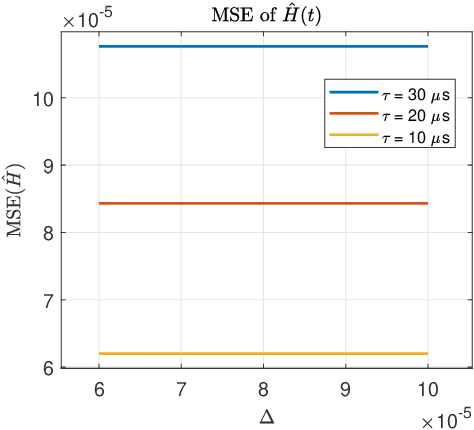
An algorithm for continuous time-delay estimation from sampled output data and known input of finite energy is presented. The continuous time-delay modeling allows for the estimation of subsample delays. The proposed estimation algorithm consists of two steps. First, the continuous Laguerre spectrum of the output signal is estimated from discrete-time (sampled) noisy measurements. Second, an estimate of the delay value is obtained in Laguerre domain given a continuous-time description of the input. The second step of the algorithm is shown to be intrinsically biased, the bias sources are established, and the bias itself is modeled. The proposed delay estimation approach is compared in a Monte-Carlo simulation with state-of-the-art methods implemented in time, frequency, and Laguerre domain demonstrating comparable or higher accuracy for the considered case.

Noise reduction in Laguerre-domain discrete delay estimation

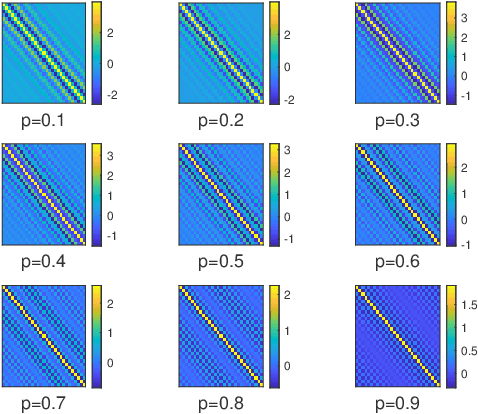
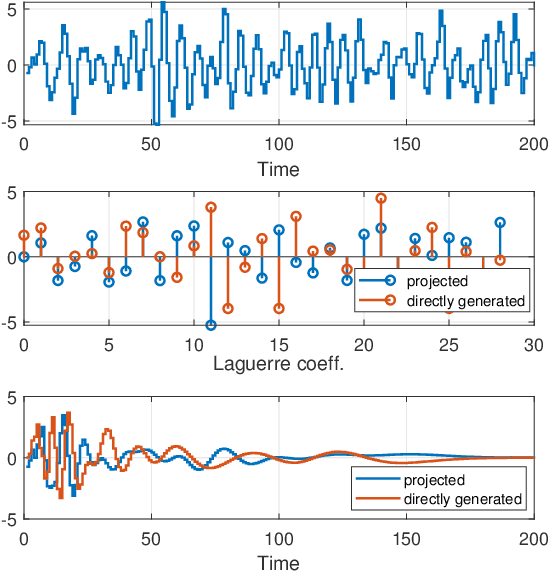
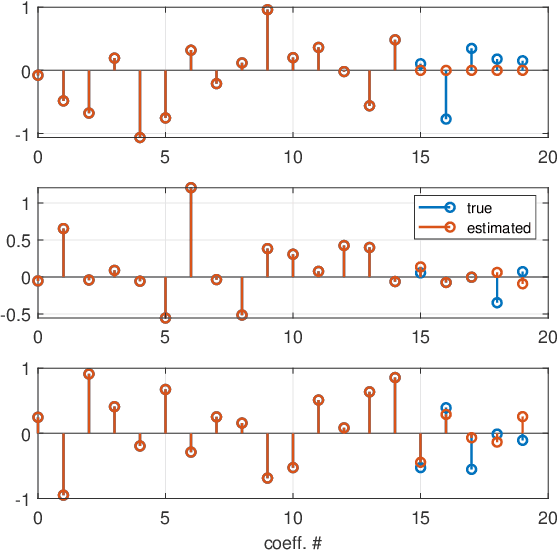
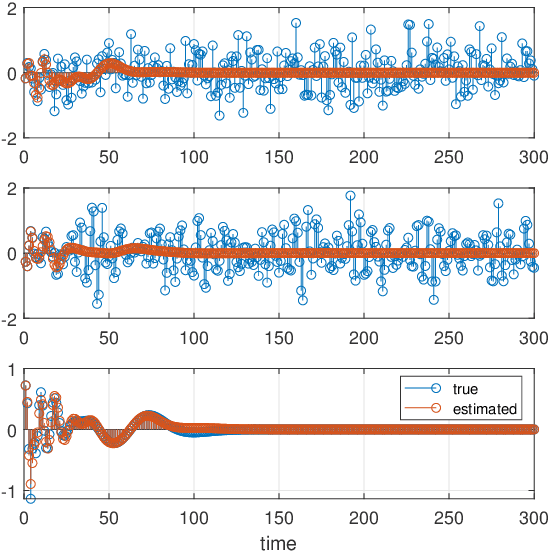
This paper introduces a stochastic framework for a recently proposed discrete-time delay estimation method in Laguerre-domain, i.e. with the delay block input and output signals being represented by the corresponding Laguerre series. A novel Laguerre domain disturbance model is devised, which allows the involved signals to be square-summable sequences and is suitable in a number of important applications. The relation to two commonly used time-domain disturbance models is clarified. Furthermore, by forming the input signal in a certain way, the signal shape of an additive output disturbance can be estimated and utilized for noise reduction. It is demonstrated that a significant improvement in the delay estimation error is achieved when the noise sequence is correlated. The noise reduction approach is applicable to other Laguerre-domain problems than pure delay estimation.

DeepBayes -- an estimator for parameter estimation in stochastic nonlinear dynamical models

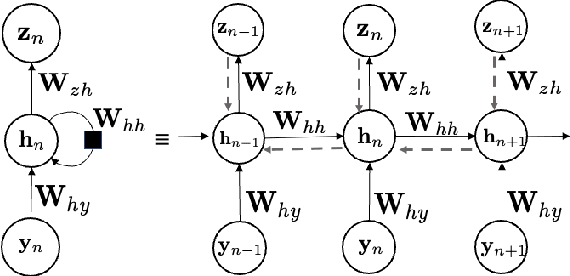
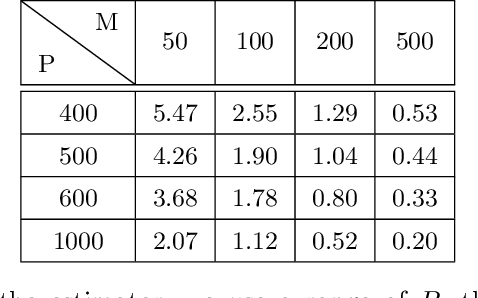
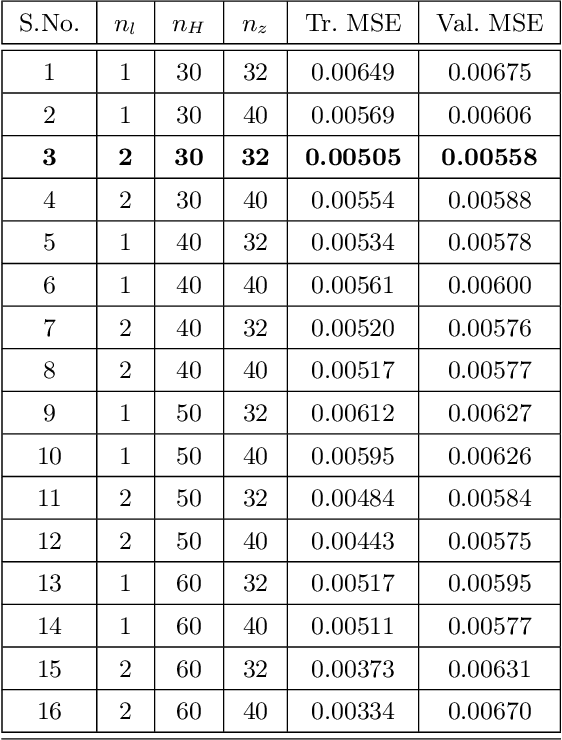
Stochastic nonlinear dynamical systems are ubiquitous in modern, real-world applications. Yet, estimating the unknown parameters of stochastic, nonlinear dynamical models remains a challenging problem. The majority of existing methods employ maximum likelihood or Bayesian estimation. However, these methods suffer from some limitations, most notably the substantial computational time for inference coupled with limited flexibility in application. In this work, we propose DeepBayes estimators that leverage the power of deep recurrent neural networks in learning an estimator. The method consists of first training a recurrent neural network to minimize the mean-squared estimation error over a set of synthetically generated data using models drawn from the model set of interest. The a priori trained estimator can then be used directly for inference by evaluating the network with the estimation data. The deep recurrent neural network architectures can be trained offline and ensure significant time savings during inference. We experiment with two popular recurrent neural networks -- long short term memory network (LSTM) and gated recurrent unit (GRU). We demonstrate the applicability of our proposed method on different example models and perform detailed comparisons with state-of-the-art approaches. We also provide a study on a real-world nonlinear benchmark problem. The experimental evaluations show that the proposed approach is asymptotically as good as the Bayes estimator.