Online Agnostic Multiclass Boosting

Boosting is a fundamental approach in machine learning that enjoys both strong theoretical and practical guarantees. At a high-level, boosting algorithms cleverly aggregate weak learners to generate predictions with arbitrarily high accuracy. In this way, boosting algorithms convert weak learners into strong ones. Recently, Brukhim et al. extended boosting to the online agnostic binary classification setting. A key ingredient in their approach is a clean and simple reduction to online convex optimization, one that efficiently converts an arbitrary online convex optimizer to an agnostic online booster. In this work, we extend this reduction to multiclass problems and give the first boosting algorithm for online agnostic mutliclass classification. Our reduction also enables the construction of algorithms for statistical agnostic, online realizable, and statistical realizable multiclass boosting.

An Optimization-based Algorithm for Non-stationary Kernel Bandits without Prior Knowledge

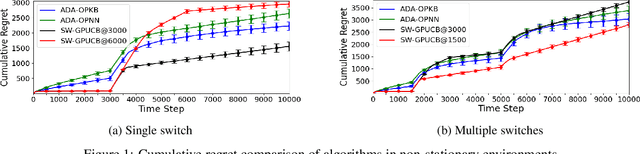
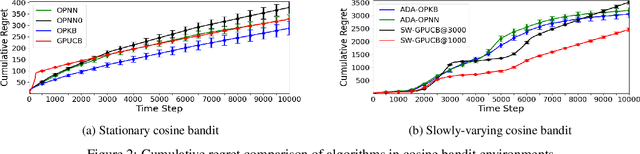
We propose an algorithm for non-stationary kernel bandits that does not require prior knowledge of the degree of non-stationarity. The algorithm follows randomized strategies obtained by solving optimization problems that balance exploration and exploitation. It adapts to non-stationarity by restarting when a change in the reward function is detected. Our algorithm enjoys a tighter dynamic regret bound than previous work on the non-stationary kernel bandit setting. Moreover, when applied to the non-stationary linear bandit setting by using a linear kernel, our algorithm is nearly minimax optimal, solving an open problem in the non-stationary linear bandit literature. We extend our algorithm to use a neural network for dynamically adapting the feature mapping to observed data. We prove a dynamic regret bound of the extension using the neural tangent kernel theory. We demonstrate empirically that our algorithm and the extension can adapt to varying degrees of non-stationarity.

Achieving Representative Data via Convex Hull Feasibility Sampling Algorithms

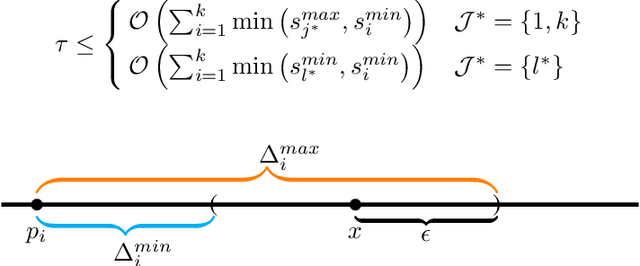
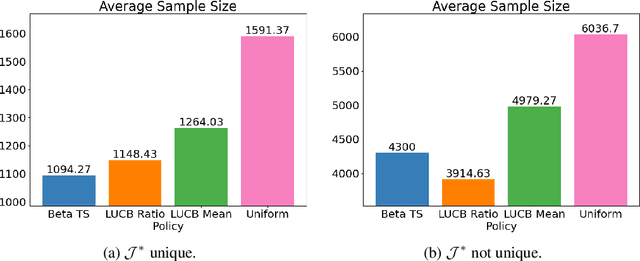
Sampling biases in training data are a major source of algorithmic biases in machine learning systems. Although there are many methods that attempt to mitigate such algorithmic biases during training, the most direct and obvious way is simply collecting more representative training data. In this paper, we consider the task of assembling a training dataset in which minority groups are adequately represented from a given set of data sources. In essence, this is an adaptive sampling problem to determine if a given point lies in the convex hull of the means from a set of unknown distributions. We present adaptive sampling methods to determine, with high confidence, whether it is possible to assemble a representative dataset from the given data sources. We also demonstrate the efficacy of our policies in simulations in the Bernoulli and a multinomial setting.

Joint Learning of Linear Time-Invariant Dynamical Systems

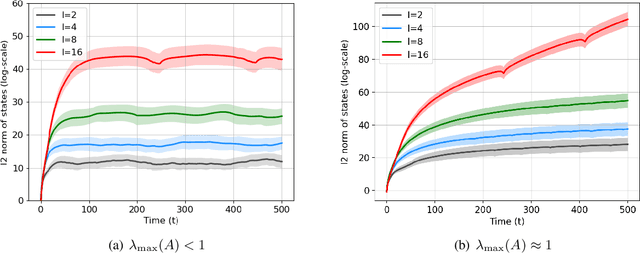
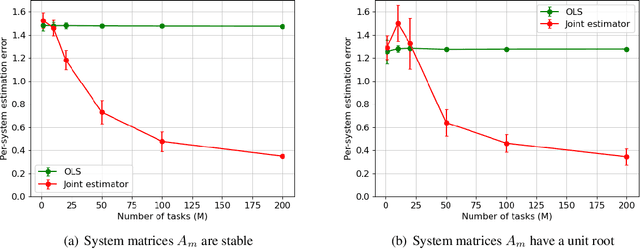
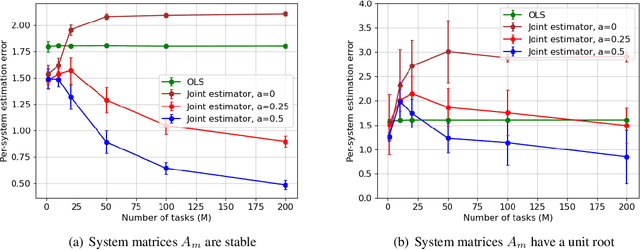
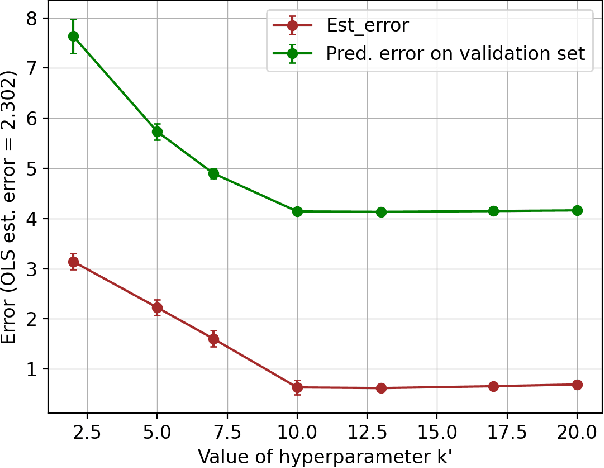
Learning the parameters of a linear time-invariant dynamical system (LTIDS) is a problem of current interest. In many applications, one is interested in jointly learning the parameters of multiple related LTIDS, which remains unexplored to date. To that end, we develop a joint estimator for learning the transition matrices of LTIDS that share common basis matrices. Further, we establish finite-time error bounds that depend on the underlying sample size, dimension, number of tasks, and spectral properties of the transition matrices. The results are obtained under mild regularity assumptions and showcase the gains from pooling information across LTIDS, in comparison to learning each system separately. We also study the impact of misspecifying the joint structure of the transition matrices and show that the established results are robust in the presence of moderate misspecifications.

Balancing Adaptability and Non-exploitability in Repeated Games

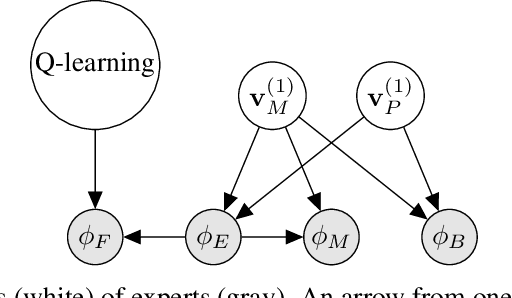
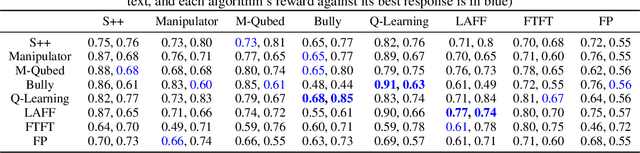
We study the problem of guaranteeing low regret in repeated games against an opponent with unknown membership in one of several classes. We add the constraint that our algorithm is non-exploitable, in that the opponent lacks an incentive to use an algorithm against which we cannot achieve rewards exceeding some "fair" value. Our solution is an expert algorithm (LAFF) that searches within a set of sub-algorithms that are optimal for each opponent class and uses a punishment policy upon detecting evidence of exploitation by the opponent. With benchmarks that depend on the opponent class, we show that LAFF has sublinear regret uniformly over the possible opponents, except exploitative ones, for which we guarantee that the opponent has linear regret. To our knowledge, this work is the first to provide guarantees for both regret and non-exploitability in multi-agent learning.

On the Statistical Benefits of Curriculum Learning

Curriculum learning (CL) is a commonly used machine learning training strategy. However, we still lack a clear theoretical understanding of CL's benefits. In this paper, we study the benefits of CL in the multitask linear regression problem under both structured and unstructured settings. For both settings, we derive the minimax rates for CL with the oracle that provides the optimal curriculum and without the oracle, where the agent has to adaptively learn a good curriculum. Our results reveal that adaptive learning can be fundamentally harder than the oracle learning in the unstructured setting, but it merely introduces a small extra term in the structured setting. To connect theory with practice, we provide justification for a popular empirical method that selects tasks with highest local prediction gain by comparing its guarantees with the minimax rates mentioned above.

Online Learning in Adversarial MDPs: Is the Communicating Case Harder than Ergodic?

We study online learning in adversarial communicating Markov Decision Processes with full information. We give an algorithm that achieves a regret of $O(\sqrt{T})$ with respect to the best fixed deterministic policy in hindsight when the transitions are deterministic. We also prove a regret lower bound in this setting which is tight up to polynomial factors in the MDP parameters. We also give an inefficient algorithm that achieves $O(\sqrt{T})$ regret in communicating MDPs (with an additional mild restriction on the transition dynamics).

Bandit Algorithms for Precision Medicine

The Oxford English Dictionary defines precision medicine as "medical care designed to optimize efficiency or therapeutic benefit for particular groups of patients, especially by using genetic or molecular profiling." It is not an entirely new idea: physicians from ancient times have recognized that medical treatment needs to consider individual variations in patient characteristics. However, the modern precision medicine movement has been enabled by a confluence of events: scientific advances in fields such as genetics and pharmacology, technological advances in mobile devices and wearable sensors, and methodological advances in computing and data sciences. This chapter is about bandit algorithms: an area of data science of special relevance to precision medicine. With their roots in the seminal work of Bellman, Robbins, Lai and others, bandit algorithms have come to occupy a central place in modern data science ( Lattimore and Szepesvari, 2020). Bandit algorithms can be used in any situation where treatment decisions need to be made to optimize some health outcome. Since precision medicine focuses on the use of patient characteristics to guide treatment, contextual bandit algorithms are especially useful since they are designed to take such information into account. The role of bandit algorithms in areas of precision medicine such as mobile health and digital phenotyping has been reviewed before (Tewari and Murphy, 2017; Rabbi et al., 2019). Since these reviews were published, bandit algorithms have continued to find uses in mobile health and several new topics have emerged in the research on bandit algorithms. This chapter is written for quantitative researchers in fields such as statistics, machine learning, and operations research who might be interested in knowing more about the algorithmic and mathematical details of bandit algorithms that have been used in mobile health.

Weighted Gaussian Process Bandits for Non-stationary Environments

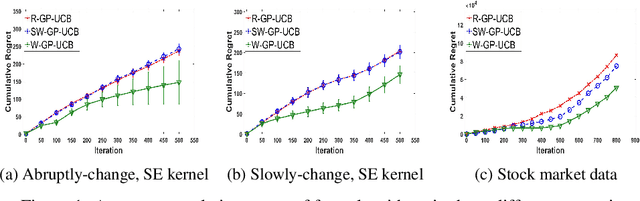
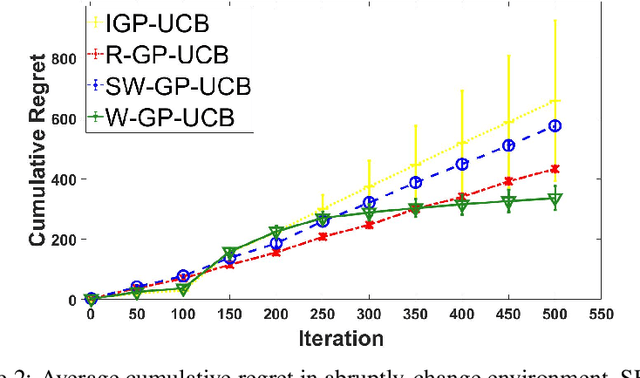
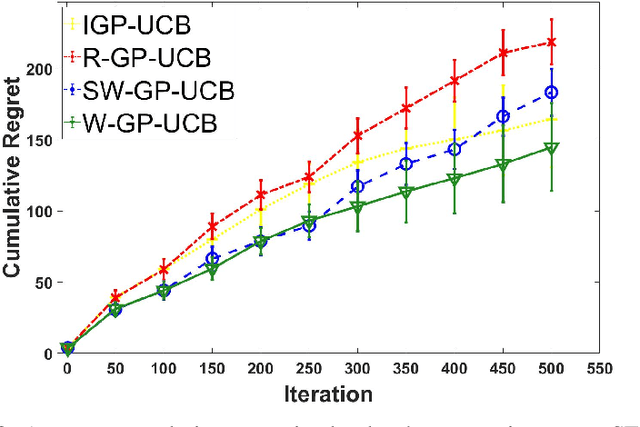
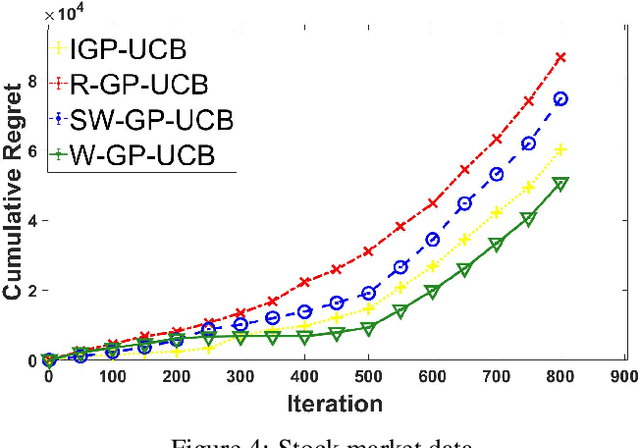
In this paper, we consider the Gaussian process (GP) bandit optimization problem in a non-stationary environment. To capture external changes, the black-box function is allowed to be time-varying within a reproducing kernel Hilbert space (RKHS). To this end, we develop WGP-UCB, a novel UCB-type algorithm based on weighted Gaussian process regression. A key challenge is how to cope with infinite-dimensional feature maps. To that end, we leverage kernel approximation techniques to prove a sublinear regret bound, which is the first (frequentist) sublinear regret guarantee on weighted time-varying bandits with general nonlinear rewards. This result generalizes both non-stationary linear bandits and standard GP-UCB algorithms. Further, a novel concentration inequality is achieved for weighted Gaussian process regression with general weights. We also provide universal upper bounds and weight-dependent upper bounds for weighted maximum information gains. These results are potentially of independent interest for applications such as news ranking and adaptive pricing, where weights can be adopted to capture the importance or quality of data. Finally, we conduct experiments to highlight the favorable gains of the proposed algorithm in many cases when compared to existing methods.

Causal Bandits with Unknown Graph Structure

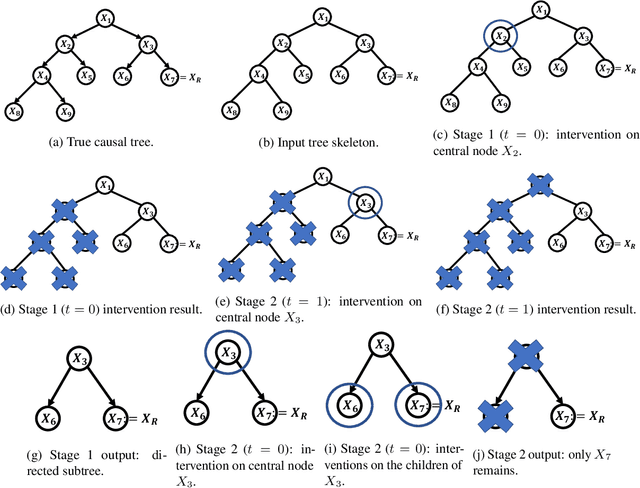
In causal bandit problems, the action set consists of interventions on variables of a causal graph. Several researchers have recently studied such bandit problems and pointed out their practical applications. However, all existing works rely on a restrictive and impractical assumption that the learner is given full knowledge of the causal graph structure upfront. In this paper, we develop novel causal bandit algorithms without knowing the causal graph. Our algorithms work well for causal trees, causal forests and a general class of causal graphs. The regret guarantees of our algorithms greatly improve upon those of standard multi-armed bandit (MAB) algorithms under mild conditions. Lastly, we prove our mild conditions are necessary: without them one cannot do better than standard MAB bandit algorithms.