Offline Constrained Reinforcement Learning under Partial Data Coverage

We study offline constrained reinforcement learning (RL) with general function approximation. We aim to learn a policy from a pre-collected dataset that maximizes the expected discounted cumulative reward for a primary reward signal while ensuring that expected discounted returns for multiple auxiliary reward signals are above predefined thresholds. Existing algorithms either require fully exploratory data, are computationally inefficient, or depend on an additional auxiliary function classes to obtain an $\epsilon$-optimal policy with sample complexity $O(\epsilon^{-2})$. In this paper, we propose an oracle-efficient primal-dual algorithm based on a linear programming (LP) formulation, achieving $O(\epsilon^{-2})$ sample complexity under partial data coverage. By introducing a realizability assumption, our approach ensures that all saddle points of the Lagrangian are optimal, removing the need for regularization that complicated prior analyses. Through Lagrangian decomposition, our method extracts policies without requiring knowledge of the data-generating distribution, enhancing practical applicability.

Generator-Mediated Bandits: Thompson Sampling for GenAI-Powered Adaptive Interventions

Recent advances in generative artificial intelligence (GenAI) models have enabled the generation of personalized content that adapts to up-to-date user context. While personalized decision systems are often modeled using bandit formulations, the integration of GenAI introduces new structure into otherwise classical sequential learning problems. In GenAI-powered interventions, the agent selects a query, but the environment experiences a stochastic response drawn from the generative model. Standard bandit methods do not explicitly account for this structure, where actions influence rewards only through stochastic, observed treatments. We introduce generator-mediated bandit-Thompson sampling (GAMBITTS), a bandit approach designed for this action/treatment split, using mobile health interventions with large language model-generated text as a motivating case study. GAMBITTS explicitly models both the treatment and reward generation processes, using information in the delivered treatment to accelerate policy learning relative to standard methods. We establish regret bounds for GAMBITTS by decomposing sources of uncertainty in treatment and reward, identifying conditions where it achieves stronger guarantees than standard bandit approaches. In simulation studies, GAMBITTS consistently outperforms conventional algorithms by leveraging observed treatments to more accurately estimate expected rewards.

A Computationally Efficient Algorithm for Infinite-Horizon Average-Reward Linear MDPs

We study reinforcement learning in infinite-horizon average-reward settings with linear MDPs. Previous work addresses this problem by approximating the average-reward setting by discounted setting and employing a value iteration-based algorithm that uses clipping to constrain the span of the value function for improved statistical efficiency. However, the clipping procedure requires computing the minimum of the value function over the entire state space, which is prohibitive since the state space in linear MDP setting can be large or even infinite. In this paper, we introduce a value iteration method with efficient clipping operation that only requires computing the minimum of value functions over the set of states visited by the algorithm. Our algorithm enjoys the same regret bound as the previous work while being computationally efficient, with computational complexity that is independent of the size of the state space.

A Primal-Dual Algorithm for Offline Constrained Reinforcement Learning with Low-Rank MDPs

Offline reinforcement learning (RL) aims to learn a policy that maximizes the expected cumulative reward using a pre-collected dataset. Offline RL with low-rank MDPs or general function approximation has been widely studied recently, but existing algorithms with sample complexity $O(\epsilon^{-2})$ for finding an $\epsilon$-optimal policy either require a uniform data coverage assumptions or are computationally inefficient. In this paper, we propose a primal dual algorithm for offline RL with low-rank MDPs in the discounted infinite-horizon setting. Our algorithm is the first computationally efficient algorithm in this setting that achieves sample complexity of $O(\epsilon^{-2})$ with partial data coverage assumption. This improves upon a recent work that requires $O(\epsilon^{-4})$ samples. Moreover, our algorithm extends the previous work to the offline constrained RL setting by supporting constraints on additional reward signals.

A Primal-Dual-Critic Algorithm for Offline Constrained Reinforcement Learning

Offline constrained reinforcement learning (RL) aims to learn a policy that maximizes the expected cumulative reward subject to constraints on expected value of cost functions using an existing dataset. In this paper, we propose Primal-Dual-Critic Algorithm (PDCA), a novel algorithm for offline constrained RL with general function approximation. PDCA runs a primal-dual algorithm on the Lagrangian function estimated by critics. The primal player employs a no-regret policy optimization oracle to maximize the Lagrangian estimate given any choices of the critics and the dual player. The dual player employs a no-regret online linear optimization oracle to minimize the Lagrangian estimate given any choices of the critics and the primal player. We show that PDCA can successfully find a near saddle point of the Lagrangian, which is nearly optimal for the constrained RL problem. Unlike previous work that requires concentrability and strong Bellman completeness assumptions, PDCA only requires concentrability and value function/marginalized importance weight realizability assumptions.

An Optimization-based Algorithm for Non-stationary Kernel Bandits without Prior Knowledge

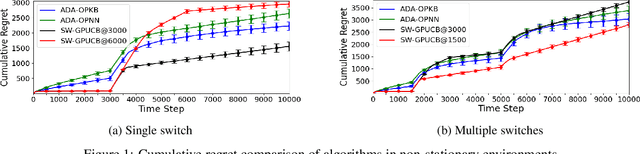
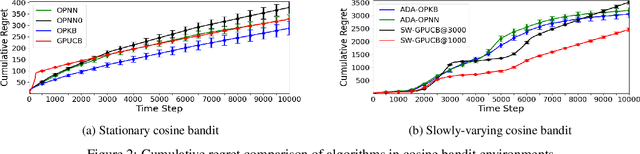
We propose an algorithm for non-stationary kernel bandits that does not require prior knowledge of the degree of non-stationarity. The algorithm follows randomized strategies obtained by solving optimization problems that balance exploration and exploitation. It adapts to non-stationarity by restarting when a change in the reward function is detected. Our algorithm enjoys a tighter dynamic regret bound than previous work on the non-stationary kernel bandit setting. Moreover, when applied to the non-stationary linear bandit setting by using a linear kernel, our algorithm is nearly minimax optimal, solving an open problem in the non-stationary linear bandit literature. We extend our algorithm to use a neural network for dynamically adapting the feature mapping to observed data. We prove a dynamic regret bound of the extension using the neural tangent kernel theory. We demonstrate empirically that our algorithm and the extension can adapt to varying degrees of non-stationarity.