Random Cycle Coding: Lossless Compression of Cluster Assignments via Bits-Back Coding

We present an optimal method for encoding cluster assignments of arbitrary data sets. Our method, Random Cycle Coding (RCC), encodes data sequentially and sends assignment information as cycles of the permutation defined by the order of encoded elements. RCC does not require any training and its worst-case complexity scales quasi-linearly with the size of the largest cluster. We characterize the achievable bit rates as a function of cluster sizes and number of elements, showing RCC consistently outperforms previous methods while requiring less compute and memory resources. Experiments show RCC can save up to 2 bytes per element when applied to vector databases, and removes the need for assigning integer ids to identify vectors, translating to savings of up to 70% in vector database systems for similarity search applications.

Probabilistic Inference in Language Models via Twisted Sequential Monte Carlo

Numerous capability and safety techniques of Large Language Models (LLMs), including RLHF, automated red-teaming, prompt engineering, and infilling, can be cast as sampling from an unnormalized target distribution defined by a given reward or potential function over the full sequence. In this work, we leverage the rich toolkit of Sequential Monte Carlo (SMC) for these probabilistic inference problems. In particular, we use learned twist functions to estimate the expected future value of the potential at each timestep, which enables us to focus inference-time computation on promising partial sequences. We propose a novel contrastive method for learning the twist functions, and establish connections with the rich literature of soft reinforcement learning. As a complementary application of our twisted SMC framework, we present methods for evaluating the accuracy of language model inference techniques using novel bidirectional SMC bounds on the log partition function. These bounds can be used to estimate the KL divergence between the inference and target distributions in both directions. We apply our inference evaluation techniques to show that twisted SMC is effective for sampling undesirable outputs from a pretrained model (a useful component of harmlessness training and automated red-teaming), generating reviews with varied sentiment, and performing infilling tasks.

Can We Remove the Square-Root in Adaptive Gradient Methods? A Second-Order Perspective

Adaptive gradient optimizers like Adam(W) are the default training algorithms for many deep learning architectures, such as transformers. Their diagonal preconditioner is based on the gradient outer product which is incorporated into the parameter update via a square root. While these methods are often motivated as approximate second-order methods, the square root represents a fundamental difference. In this work, we investigate how the behavior of adaptive methods changes when we remove the root, i.e. strengthen their second-order motivation. Surprisingly, we find that such square-root-free adaptive methods close the generalization gap to SGD on convolutional architectures, while maintaining their root-based counterpart's performance on transformers. The second-order perspective also has practical benefits for the development of adaptive methods with non-diagonal preconditioner. In contrast to root-based counterparts like Shampoo, they do not require numerically unstable matrix square roots and therefore work well in low precision, which we demonstrate empirically. This raises important questions regarding the currently overlooked role of adaptivity for the success of adaptive methods since the success is often attributed to sign descent induced by the root.

Structured Inverse-Free Natural Gradient: Memory-Efficient & Numerically-Stable KFAC for Large Neural Nets

Second-order methods for deep learning -- such as KFAC -- can be useful for neural net training. However, they are often memory-inefficient and numerically unstable for low-precision training since their preconditioning Kronecker factors are dense, and require high-precision matrix inversion or decomposition. Consequently, such methods are not widely used for training large neural networks such as transformer-based models. We address these two issues by (i) formulating an inverse-free update of KFAC and (ii) imposing structures in each of the Kronecker factors, resulting in a method we term structured inverse-free natural gradient descent (SINGD). On large modern neural networks, we show that, in contrast to KFAC, SINGD is memory efficient and numerically robust, and often outperforms AdamW even in half precision. Hence, our work closes a gap between first-order and second-order methods in modern low precision training for large neural nets.

A Computational Framework for Solving Wasserstein Lagrangian Flows

The dynamical formulation of the optimal transport can be extended through various choices of the underlying geometry ($\textit{kinetic energy}$), and the regularization of density paths ($\textit{potential energy}$). These combinations yield different variational problems ($\textit{Lagrangians}$), encompassing many variations of the optimal transport problem such as the Schr\"odinger bridge, unbalanced optimal transport, and optimal transport with physical constraints, among others. In general, the optimal density path is unknown, and solving these variational problems can be computationally challenging. Leveraging the dual formulation of the Lagrangians, we propose a novel deep learning based framework approaching all of these problems from a unified perspective. Our method does not require simulating or backpropagating through the trajectories of the learned dynamics, and does not need access to optimal couplings. We showcase the versatility of the proposed framework by outperforming previous approaches for the single-cell trajectory inference, where incorporating prior knowledge into the dynamics is crucial for correct predictions.

Wasserstein Quantum Monte Carlo: A Novel Approach for Solving the Quantum Many-Body Schrödinger Equation

Solving the quantum many-body Schr\"odinger equation is a fundamental and challenging problem in the fields of quantum physics, quantum chemistry, and material sciences. One of the common computational approaches to this problem is Quantum Variational Monte Carlo (QVMC), in which ground-state solutions are obtained by minimizing the energy of the system within a restricted family of parameterized wave functions. Deep learning methods partially address the limitations of traditional QVMC by representing a rich family of wave functions in terms of neural networks. However, the optimization objective in QVMC remains notoriously hard to minimize and requires second-order optimization methods such as natural gradient. In this paper, we first reformulate energy functional minimization in the space of Born distributions corresponding to particle-permutation (anti-)symmetric wave functions, rather than the space of wave functions. We then interpret QVMC as the Fisher-Rao gradient flow in this distributional space, followed by a projection step onto the variational manifold. This perspective provides us with a principled framework to derive new QMC algorithms, by endowing the distributional space with better metrics, and following the projected gradient flow induced by those metrics. More specifically, we propose "Wasserstein Quantum Monte Carlo" (WQMC), which uses the gradient flow induced by the Wasserstein metric, rather than Fisher-Rao metric, and corresponds to transporting the probability mass, rather than teleporting it. We demonstrate empirically that the dynamics of WQMC results in faster convergence to the ground state of molecular systems.

Random Edge Coding: One-Shot Bits-Back Coding of Large Labeled Graphs

We present a one-shot method for compressing large labeled graphs called Random Edge Coding. When paired with a parameter-free model based on P\'olya's Urn, the worst-case computational and memory complexities scale quasi-linearly and linearly with the number of observed edges, making it efficient on sparse graphs, and requires only integer arithmetic. Key to our method is bits-back coding, which is used to sample edges and vertices without replacement from the edge-list in a way that preserves the structure of the graph. Optimality is proven under a class of random graph models that are invariant to permutations of the edges and of vertices within an edge. Experiments indicate Random Edge Coding can achieve competitive compression performance on real-world network datasets and scales to graphs with millions of nodes and edges.

Improving Mutual Information Estimation with Annealed and Energy-Based Bounds

Mutual information (MI) is a fundamental quantity in information theory and machine learning. However, direct estimation of MI is intractable, even if the true joint probability density for the variables of interest is known, as it involves estimating a potentially high-dimensional log partition function. In this work, we present a unifying view of existing MI bounds from the perspective of importance sampling, and propose three novel bounds based on this approach. Since accurate estimation of MI without density information requires a sample size exponential in the true MI, we assume either a single marginal or the full joint density information is known. In settings where the full joint density is available, we propose Multi-Sample Annealed Importance Sampling (AIS) bounds on MI, which we demonstrate can tightly estimate large values of MI in our experiments. In settings where only a single marginal distribution is known, we propose Generalized IWAE (GIWAE) and MINE-AIS bounds. Our GIWAE bound unifies variational and contrastive bounds in a single framework that generalizes InfoNCE, IWAE, and Barber-Agakov bounds. Our MINE-AIS method improves upon existing energy-based methods such as MINE-DV and MINE-F by directly optimizing a tighter lower bound on MI. MINE-AIS uses MCMC sampling to estimate gradients for training and Multi-Sample AIS for evaluating the bound. Our methods are particularly suitable for evaluating MI in deep generative models, since explicit forms of the marginal or joint densities are often available. We evaluate our bounds on estimating the MI of VAEs and GANs trained on the MNIST and CIFAR datasets, and showcase significant gains over existing bounds in these challenging settings with high ground truth MI.

Quantum HyperNetworks: Training Binary Neural Networks in Quantum Superposition

Binary neural networks, i.e., neural networks whose parameters and activations are constrained to only two possible values, offer a compelling avenue for the deployment of deep learning models on energy- and memory-limited devices. However, their training, architectural design, and hyperparameter tuning remain challenging as these involve multiple computationally expensive combinatorial optimization problems. Here we introduce quantum hypernetworks as a mechanism to train binary neural networks on quantum computers, which unify the search over parameters, hyperparameters, and architectures in a single optimization loop. Through classical simulations, we demonstrate that of our approach effectively finds optimal parameters, hyperparameters and architectural choices with high probability on classification problems including a two-dimensional Gaussian dataset and a scaled-down version of the MNIST handwritten digits. We represent our quantum hypernetworks as variational quantum circuits, and find that an optimal circuit depth maximizes the probability of finding performant binary neural networks. Our unified approach provides an immense scope for other applications in the field of machine learning.

Action Matching: A Variational Method for Learning Stochastic Dynamics from Samples

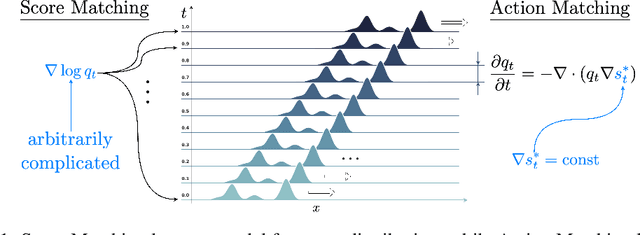
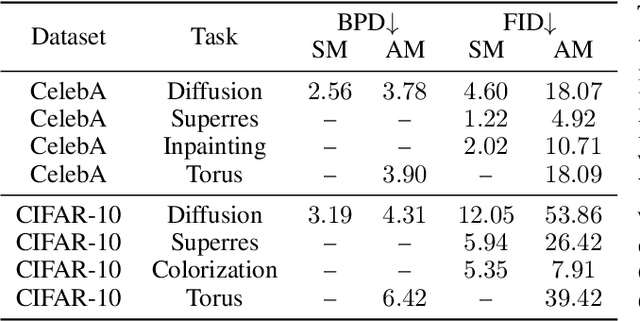
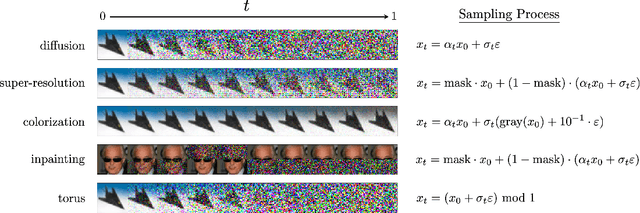
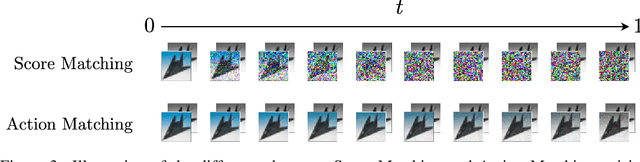
Stochastic dynamics are ubiquitous in many fields of science, from the evolution of quantum systems in physics to diffusion-based models in machine learning. Existing methods such as score matching can be used to simulate these physical processes by assuming that the dynamics is a diffusion, which is not always the case. In this work, we propose a method called "Action Matching" that enables us to learn a much broader family of stochastic dynamics. Our method requires access only to samples from different time-steps, makes no explicit assumptions about the underlying dynamics, and can be applied even when samples are uncorrelated (i.e., are not part of a trajectory). Action Matching directly learns an underlying mechanism to move samples in time without modeling the distributions at each time-step. In this work, we showcase how Action Matching can be used for several computer vision tasks such as generative modeling, super-resolution, colorization, and inpainting; and further discuss potential applications in other areas of science.