Ab-initio variational wave functions for the time-dependent many-electron Schrödinger equation

Describing the dynamics of many-electron quantum systems is crucial for applications such as predicting electronic structures in quantum chemistry, the properties of condensed matter systems, and the behaviors of complex materials. However, the real-time evolution of non-equilibrium quantum electronic systems poses a significant challenge for theoretical and computational approaches, due to the system's exploration of a vast configuration space. This work introduces a variational approach for fermionic time-dependent wave functions, surpassing mean-field approximations by capturing many-body correlations. The proposed methodology involves parameterizing the time-evolving quantum state, enabling the approximation of the state's evolution. To account for electron correlations, we employ time-dependent Jastrow factors and backflow transformations. We also show that we can incorporate neural networks to parameterize these functions. The time-dependent variational Monte Carlo technique is employed to efficiently compute the optimal time-dependent parameters. The approach is demonstrated in three distinct systems: the solvable harmonic interaction model, the dynamics of a diatomic molecule in intense laser fields, and a quenched quantum dot. In all cases, we show clear signatures of many-body correlations in the dynamics not captured by mean-field methods. The results showcase the ability of our variational approach to accurately capture the time evolution of quantum states, providing insight into the quantum dynamics of interacting electronic systems, beyond the capabilities of mean-field.

Wasserstein Quantum Monte Carlo: A Novel Approach for Solving the Quantum Many-Body Schrödinger Equation

Solving the quantum many-body Schr\"odinger equation is a fundamental and challenging problem in the fields of quantum physics, quantum chemistry, and material sciences. One of the common computational approaches to this problem is Quantum Variational Monte Carlo (QVMC), in which ground-state solutions are obtained by minimizing the energy of the system within a restricted family of parameterized wave functions. Deep learning methods partially address the limitations of traditional QVMC by representing a rich family of wave functions in terms of neural networks. However, the optimization objective in QVMC remains notoriously hard to minimize and requires second-order optimization methods such as natural gradient. In this paper, we first reformulate energy functional minimization in the space of Born distributions corresponding to particle-permutation (anti-)symmetric wave functions, rather than the space of wave functions. We then interpret QVMC as the Fisher-Rao gradient flow in this distributional space, followed by a projection step onto the variational manifold. This perspective provides us with a principled framework to derive new QMC algorithms, by endowing the distributional space with better metrics, and following the projected gradient flow induced by those metrics. More specifically, we propose "Wasserstein Quantum Monte Carlo" (WQMC), which uses the gradient flow induced by the Wasserstein metric, rather than Fisher-Rao metric, and corresponds to transporting the probability mass, rather than teleporting it. We demonstrate empirically that the dynamics of WQMC results in faster convergence to the ground state of molecular systems.

NetKet 3: Machine Learning Toolbox for Many-Body Quantum Systems

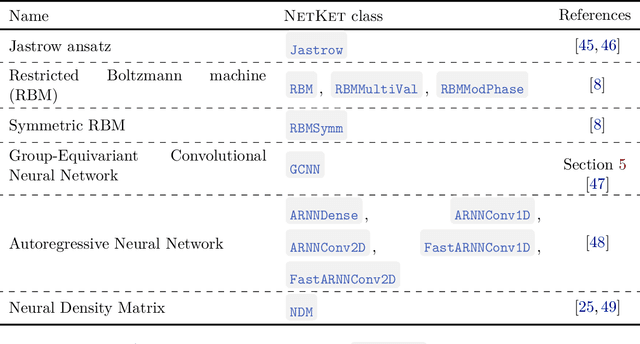
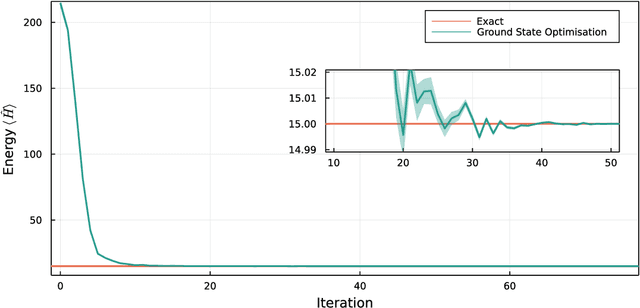
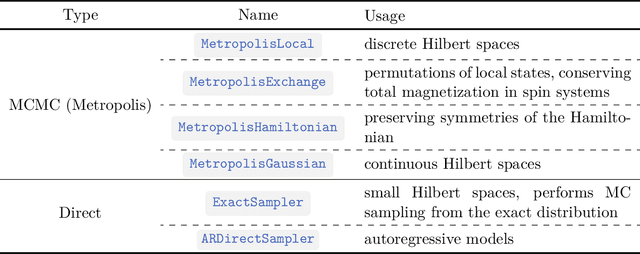
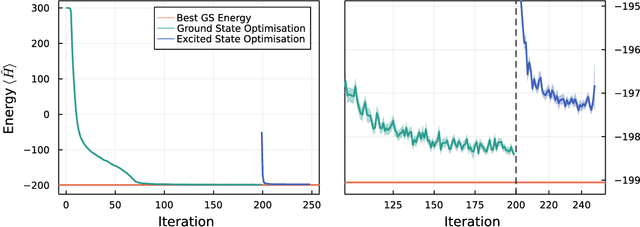
We introduce version 3 of NetKet, the machine learning toolbox for many-body quantum physics. NetKet is built around neural-network quantum states and provides efficient algorithms for their evaluation and optimization. This new version is built on top of JAX, a differentiable programming and accelerated linear algebra framework for the Python programming language. The most significant new feature is the possibility to define arbitrary neural network ans\"atze in pure Python code using the concise notation of machine-learning frameworks, which allows for just-in-time compilation as well as the implicit generation of gradients thanks to automatic differentiation. NetKet 3 also comes with support for GPU and TPU accelerators, advanced support for discrete symmetry groups, chunking to scale up to thousands of degrees of freedom, drivers for quantum dynamics applications, and improved modularity, allowing users to use only parts of the toolbox as a foundation for their own code.

Network control by a constrained external agent as a continuous optimization problem

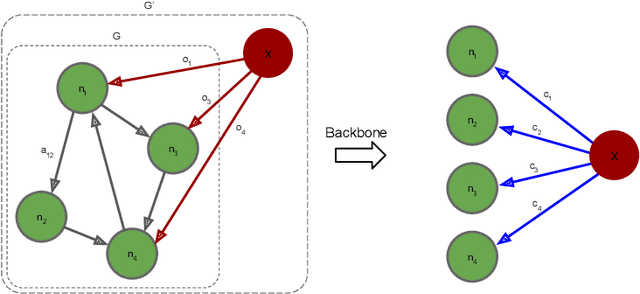
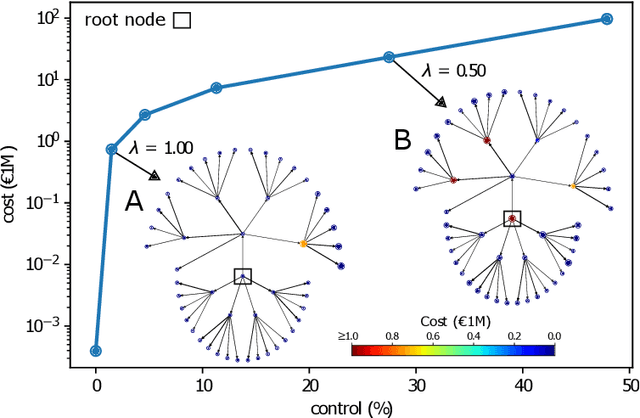
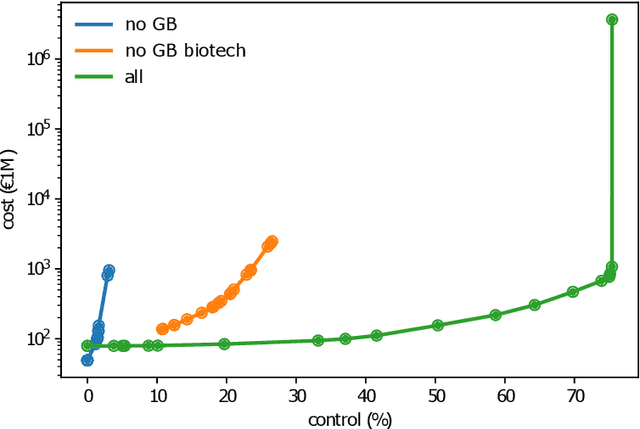
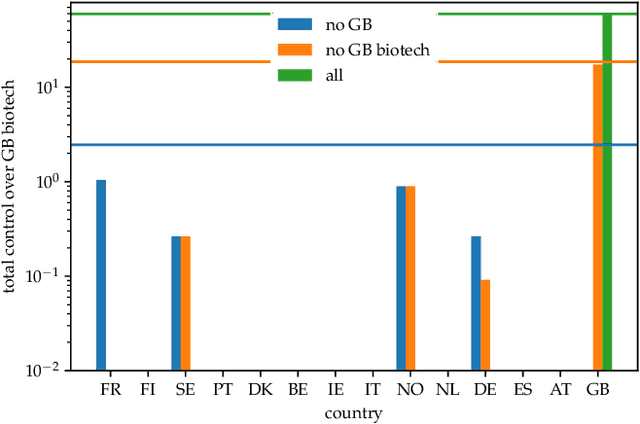
Social science studies dealing with control in networks typically resort to heuristics or describing the static control distribution. Optimal policies, however, require interventions that optimize control over a socioeconomic network subject to real-world constraints. We integrate optimisation tools from deep-learning with network science into a framework that is able to optimize such interventions in real-world networks. We demonstrate the framework in the context of corporate control, where it allows to characterize the vulnerability of strategically important corporate networks to sensitive takeovers, an important contemporaneous policy challenge. The framework produces insights that are relevant for governing real-world socioeconomic networks, and opens up new research avenues for improving our understanding and control of such complex systems.

Neural Additive Vector Autoregression Models for Causal Discovery in Time Series Data

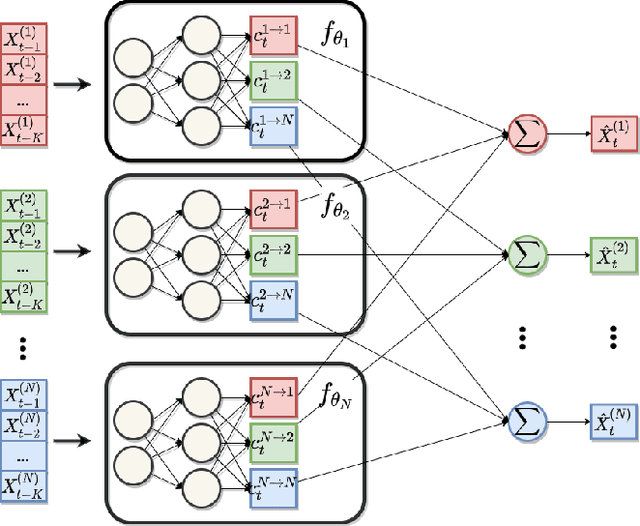
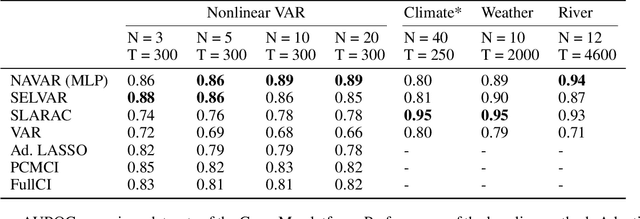
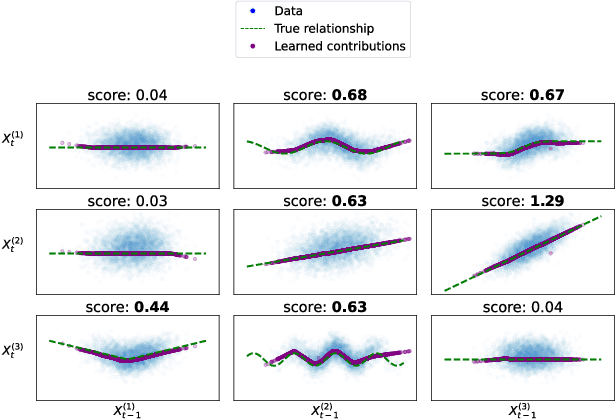
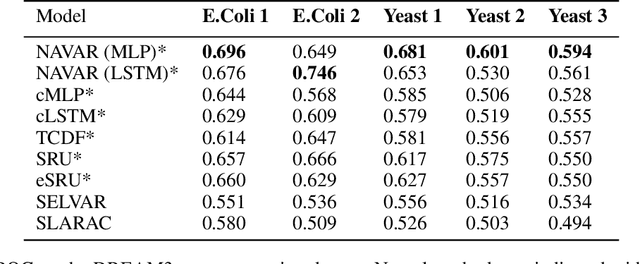
Causal structure discovery in complex dynamical systems is an important challenge for many scientific domains. Although data from (interventional) experiments is usually limited, large amounts of observational time series data sets are usually available. Current methods that learn causal structure from time series often assume linear relationships. Hence, they may fail in realistic settings that contain nonlinear relations between the variables. We propose Neural Additive Vector Autoregression (NAVAR) models, a neural approach to causal structure learning that can discover nonlinear relationships. We train deep neural networks that extract the (additive) Granger causal influences from the time evolution in multi-variate time series. The method achieves state-of-the-art results on various benchmark data sets for causal discovery, while providing clear interpretations of the mapped causal relations.