Scalable quantum dynamics compilation via quantum machine learning

Quantum dynamics compilation is an important task for improving quantum simulation efficiency: It aims to synthesize multi-qubit target dynamics into a circuit consisting of as few elementary gates as possible. Compared to deterministic methods such as Trotterization, variational quantum compilation (VQC) methods employ variational optimization to reduce gate costs while maintaining high accuracy. In this work, we explore the potential of a VQC scheme by making use of out-of-distribution generalization results in quantum machine learning (QML): By learning the action of a given many-body dynamics on a small data set of product states, we can obtain a unitary circuit that generalizes to highly entangled states such as the Haar random states. The efficiency in training allows us to use tensor network methods to compress such time-evolved product states by exploiting their low entanglement features. Our approach exceeds state-of-the-art compilation results in both system size and accuracy in one dimension ($1$D). For the first time, we extend VQC to systems on two-dimensional (2D) strips with a quasi-1D treatment, demonstrating a significant resource advantage over standard Trotterization methods, highlighting the method's promise for advancing quantum simulation tasks on near-term quantum processors.

Recurrent neural network wave functions for Rydberg atom arrays on kagome lattice

Rydberg atom array experiments have demonstrated the ability to act as powerful quantum simulators, preparing strongly-correlated phases of matter which are challenging to study for conventional computer simulations. A key direction has been the implementation of interactions on frustrated geometries, in an effort to prepare exotic many-body states such as spin liquids and glasses. In this paper, we apply two-dimensional recurrent neural network (RNN) wave functions to study the ground states of Rydberg atom arrays on the kagome lattice. We implement an annealing scheme to find the RNN variational parameters in regions of the phase diagram where exotic phases may occur, corresponding to rough optimization landscapes. For Rydberg atom array Hamiltonians studied previously on the kagome lattice, our RNN ground states show no evidence of exotic spin liquid or emergent glassy behavior. In the latter case, we argue that the presence of a non-zero Edwards-Anderson order parameter is an artifact of the long autocorrelations times experienced with quantum Monte Carlo simulations. This result emphasizes the utility of autoregressive models, such as RNNs, to explore Rydberg atom array physics on frustrated lattices and beyond.

Wasserstein Quantum Monte Carlo: A Novel Approach for Solving the Quantum Many-Body Schrödinger Equation

Solving the quantum many-body Schr\"odinger equation is a fundamental and challenging problem in the fields of quantum physics, quantum chemistry, and material sciences. One of the common computational approaches to this problem is Quantum Variational Monte Carlo (QVMC), in which ground-state solutions are obtained by minimizing the energy of the system within a restricted family of parameterized wave functions. Deep learning methods partially address the limitations of traditional QVMC by representing a rich family of wave functions in terms of neural networks. However, the optimization objective in QVMC remains notoriously hard to minimize and requires second-order optimization methods such as natural gradient. In this paper, we first reformulate energy functional minimization in the space of Born distributions corresponding to particle-permutation (anti-)symmetric wave functions, rather than the space of wave functions. We then interpret QVMC as the Fisher-Rao gradient flow in this distributional space, followed by a projection step onto the variational manifold. This perspective provides us with a principled framework to derive new QMC algorithms, by endowing the distributional space with better metrics, and following the projected gradient flow induced by those metrics. More specifically, we propose "Wasserstein Quantum Monte Carlo" (WQMC), which uses the gradient flow induced by the Wasserstein metric, rather than Fisher-Rao metric, and corresponds to transporting the probability mass, rather than teleporting it. We demonstrate empirically that the dynamics of WQMC results in faster convergence to the ground state of molecular systems.

A Framework for Demonstrating Practical Quantum Advantage: Racing Quantum against Classical Generative Models

Generative modeling has seen a rising interest in both classical and quantum machine learning, and it represents a promising candidate to obtain a practical quantum advantage in the near term. In this study, we build over a proposed framework for evaluating the generalization performance of generative models, and we establish the first quantitative comparative race towards practical quantum advantage (PQA) between classical and quantum generative models, namely Quantum Circuit Born Machines (QCBMs), Transformers (TFs), Recurrent Neural Networks (RNNs), Variational Autoencoders (VAEs), and Wasserstein Generative Adversarial Networks (WGANs). After defining four types of PQAs scenarios, we focus on what we refer to as potential PQA, aiming to compare quantum models with the best-known classical algorithms for the task at hand. We let the models race on a well-defined and application-relevant competition setting, where we illustrate and demonstrate our framework on 20 variables (qubits) generative modeling task. Our results suggest that QCBMs are more efficient in the data-limited regime than the other state-of-the-art classical generative models. Such a feature is highly desirable in a wide range of real-world applications where the available data is scarce.

Investigating Topological Order using Recurrent Neural Networks

Recurrent neural networks (RNNs), originally developed for natural language processing, hold great promise for accurately describing strongly correlated quantum many-body systems. Here, we employ 2D RNNs to investigate two prototypical quantum many-body Hamiltonians exhibiting topological order. Specifically, we demonstrate that RNN wave functions can effectively capture the topological order of the toric code and a Bose-Hubbard spin liquid on the kagome lattice by estimating their topological entanglement entropies. We also find that RNNs favor coherent superpositions of minimally-entangled states over minimally-entangled states themselves. Overall, our findings demonstrate that RNN wave functions constitute a powerful tool to study phases of matter beyond Landau's symmetry-breaking paradigm.

Quantum HyperNetworks: Training Binary Neural Networks in Quantum Superposition

Binary neural networks, i.e., neural networks whose parameters and activations are constrained to only two possible values, offer a compelling avenue for the deployment of deep learning models on energy- and memory-limited devices. However, their training, architectural design, and hyperparameter tuning remain challenging as these involve multiple computationally expensive combinatorial optimization problems. Here we introduce quantum hypernetworks as a mechanism to train binary neural networks on quantum computers, which unify the search over parameters, hyperparameters, and architectures in a single optimization loop. Through classical simulations, we demonstrate that of our approach effectively finds optimal parameters, hyperparameters and architectural choices with high probability on classification problems including a two-dimensional Gaussian dataset and a scaled-down version of the MNIST handwritten digits. We represent our quantum hypernetworks as variational quantum circuits, and find that an optimal circuit depth maximizes the probability of finding performant binary neural networks. Our unified approach provides an immense scope for other applications in the field of machine learning.

Supplementing Recurrent Neural Network Wave Functions with Symmetry and Annealing to Improve Accuracy

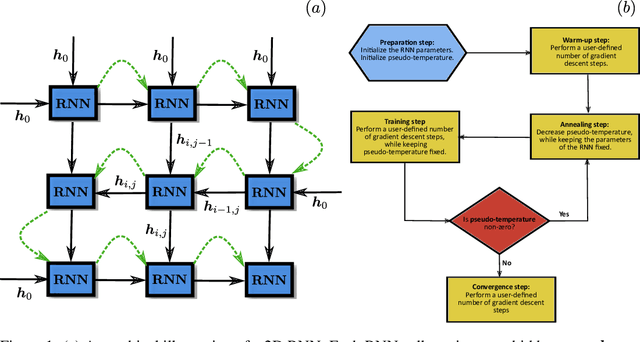
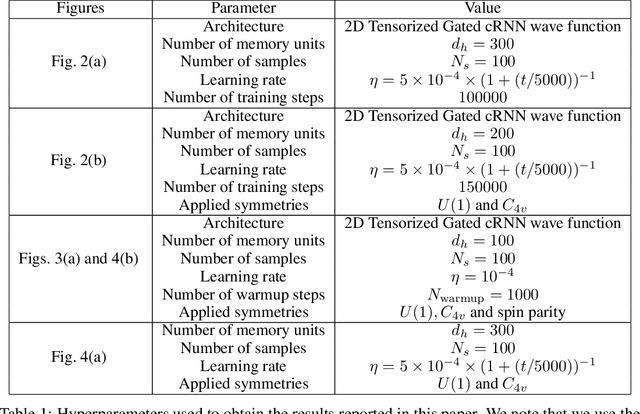
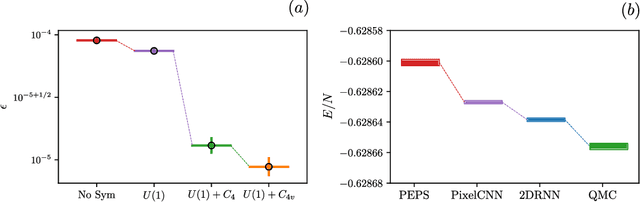
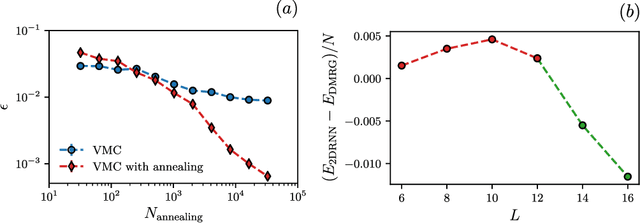
Recurrent neural networks (RNNs) are a class of neural networks that have emerged from the paradigm of artificial intelligence and has enabled lots of interesting advances in the field of natural language processing. Interestingly, these architectures were shown to be powerful ansatze to approximate the ground state of quantum systems. Here, we build over the results of [Phys. Rev. Research 2, 023358 (2020)] and construct a more powerful RNN wave function ansatz in two dimensions. We use symmetry and annealing to obtain accurate estimates of ground state energies of the two-dimensional (2D) Heisenberg model, on the square lattice and on the triangular lattice. We show that our method is superior to Density Matrix Renormalisation Group (DMRG) for system sizes larger than or equal to $14 \times 14$ on the triangular lattice.

Neural Error Mitigation of Near-Term Quantum Simulations

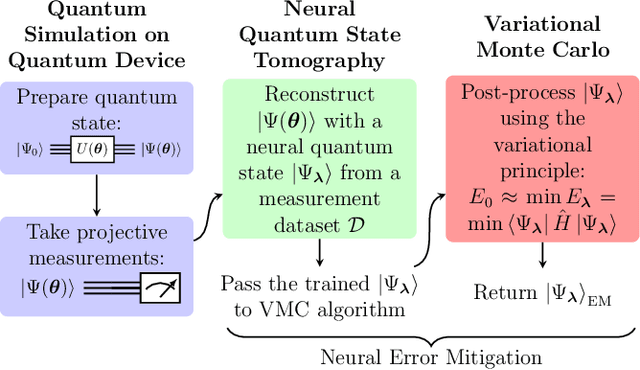
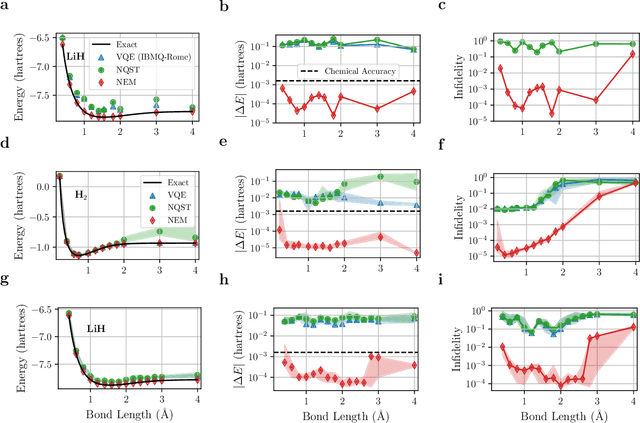
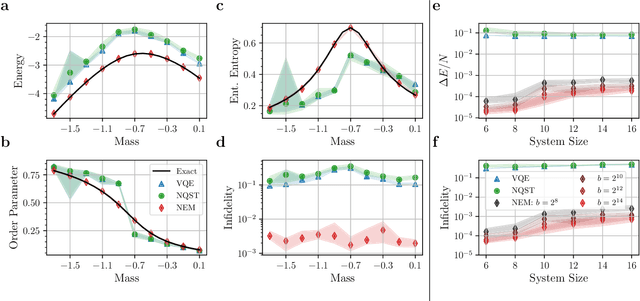
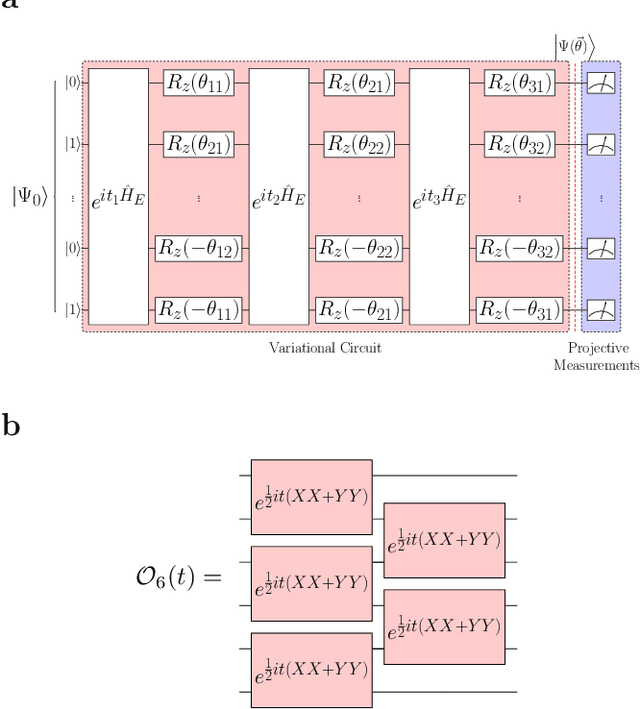
One of the promising applications of early quantum computers is the simulation of quantum systems. Variational methods for near-term quantum computers, such as the variational quantum eigensolver (VQE), are a promising approach to finding ground states of quantum systems relevant in physics, chemistry, and materials science. These approaches, however, are constrained by the effects of noise as well as the limited quantum resources of near-term quantum hardware, motivating the need for quantum error mitigation techniques to reduce the effects of noise. Here we introduce $\textit{neural error mitigation}$, a novel method that uses neural networks to improve estimates of ground states and ground-state observables obtained using VQE on near-term quantum computers. To demonstrate our method's versatility, we apply neural error mitigation to finding the ground states of H$_2$ and LiH molecular Hamiltonians, as well as the lattice Schwinger model. Our results show that neural error mitigation improves the numerical and experimental VQE computation to yield low-energy errors, low infidelities, and accurate estimations of more-complex observables like order parameters and entanglement entropy, without requiring additional quantum resources. Additionally, neural error mitigation is agnostic to both the quantum hardware and the particular noise channel, making it a versatile tool for quantum simulation. Applying quantum many-body machine learning techniques to error mitigation, our method is a promising strategy for extending the reach of near-term quantum computers to solve complex quantum simulation problems.

Variational Neural Annealing

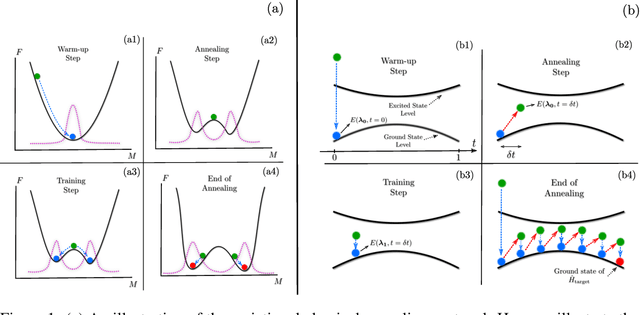
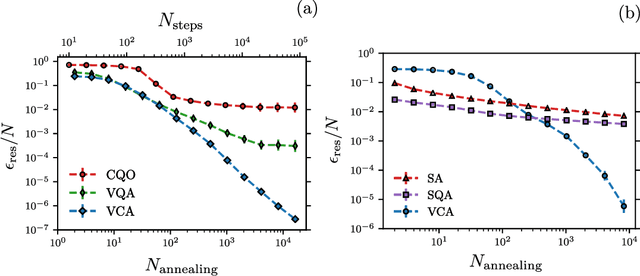
Many important challenges in science and technology can be cast as optimization problems. When viewed in a statistical physics framework, these can be tackled by simulated annealing, where a gradual cooling procedure helps search for groundstate solutions of a target Hamiltonian. While powerful, simulated annealing is known to have prohibitively slow sampling dynamics when the optimization landscape is rough or glassy. Here we show that by generalizing the target distribution with a parameterized model, an analogous annealing framework based on the variational principle can be used to search for groundstate solutions. Modern autoregressive models such as recurrent neural networks provide ideal parameterizations since they can be exactly sampled without slow dynamics even when the model encodes a rough landscape. We implement this procedure in the classical and quantum settings on several prototypical spin glass Hamiltonians, and find that it significantly outperforms traditional simulated annealing in the asymptotic limit, illustrating the potential power of this yet unexplored route to optimization.

Attention-based Quantum Tomography

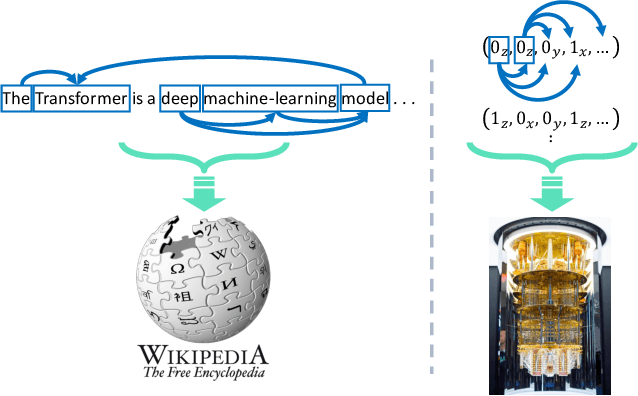
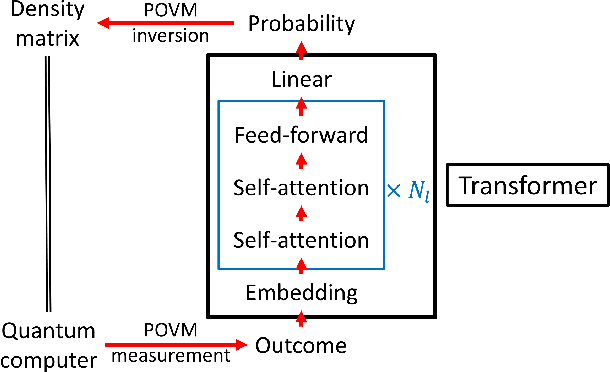
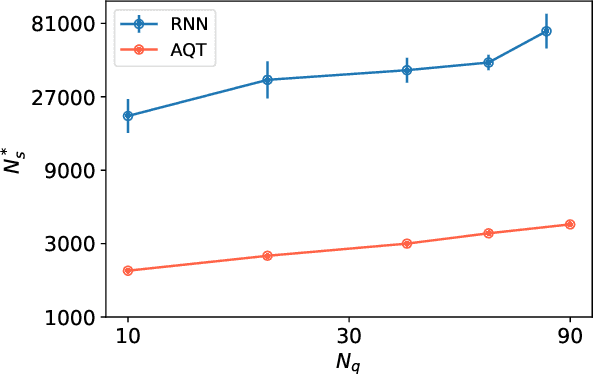
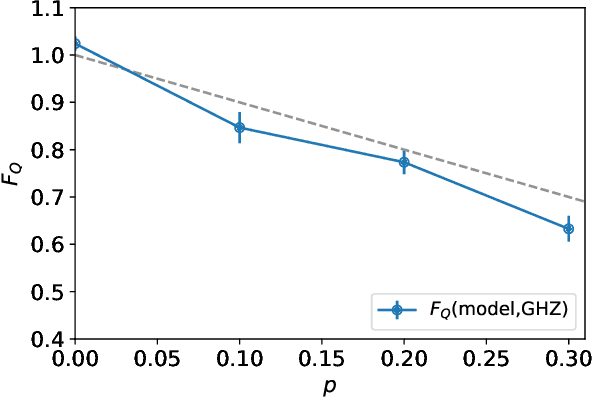
With rapid progress across platforms for quantum systems, the problem of many-body quantum state reconstruction for noisy quantum states becomes an important challenge. Recent works found promise in recasting the problem of quantum state reconstruction to learning the probability distribution of quantum state measurement vectors using generative neural network models. Here we propose the "Attention-based Quantum Tomography" (AQT), a quantum state reconstruction using an attention mechanism-based generative network that learns the mixed state density matrix of a noisy quantum state. The AQT is based on the model proposed in "Attention is all you need" by Vishwani et al (2017) that is designed to learn long-range correlations in natural language sentences and thereby outperform previous natural language processing models. We demonstrate not only that AQT outperforms earlier neural-network-based quantum state reconstruction on identical tasks but that AQT can accurately reconstruct the density matrix associated with a noisy quantum state experimentally realized in an IBMQ quantum computer. We speculate the success of the AQT stems from its ability to model quantum entanglement across the entire quantum system much as the attention model for natural language processing captures the correlations among words in a sentence.