Apertus: Democratizing Open and Compliant LLMs for Global Language Environments

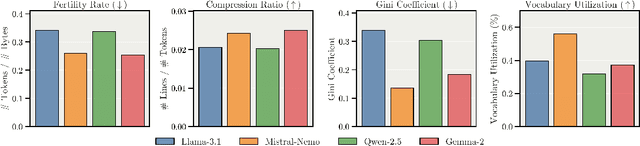
We present Apertus, a fully open suite of large language models (LLMs) designed to address two systemic shortcomings in today's open model ecosystem: data compliance and multilingual representation. Unlike many prior models that release weights without reproducible data pipelines or regard for content-owner rights, Apertus models are pretrained exclusively on openly available data, retroactively respecting robots.txt exclusions and filtering for non-permissive, toxic, and personally identifiable content. To mitigate risks of memorization, we adopt the Goldfish objective during pretraining, strongly suppressing verbatim recall of data while retaining downstream task performance. The Apertus models also expand multilingual coverage, training on 15T tokens from over 1800 languages, with ~40% of pretraining data allocated to non-English content. Released at 8B and 70B scales, Apertus approaches state-of-the-art results among fully open models on multilingual benchmarks, rivalling or surpassing open-weight counterparts. Beyond model weights, we release all scientific artifacts from our development cycle with a permissive license, including data preparation scripts, checkpoints, evaluation suites, and training code, enabling transparent audit and extension.

The Surprising Agreement Between Convex Optimization Theory and Learning-Rate Scheduling for Large Model Training

We show that learning-rate schedules for large model training behave surprisingly similar to a performance bound from non-smooth convex optimization theory. We provide a bound for the constant schedule with linear cooldown; in particular, the practical benefit of cooldown is reflected in the bound due to the absence of logarithmic terms. Further, we show that this surprisingly close match between optimization theory and practice can be exploited for learning-rate tuning: we achieve noticeable improvements for training 124M and 210M Llama-type models by (i) extending the schedule for continued training with optimal learning-rate, and (ii) transferring the optimal learning-rate across schedules.

Scaling Laws and Compute-Optimal Training Beyond Fixed Training Durations

Scale has become a main ingredient in obtaining strong machine learning models. As a result, understanding a model's scaling properties is key to effectively designing both the right training setup as well as future generations of architectures. In this work, we argue that scale and training research has been needlessly complex due to reliance on the cosine schedule, which prevents training across different lengths for the same model size. We investigate the training behavior of a direct alternative - constant learning rate and cooldowns - and find that it scales predictably and reliably similar to cosine. Additionally, we show that stochastic weight averaging yields improved performance along the training trajectory, without additional training costs, across different scales. Importantly, with these findings we demonstrate that scaling experiments can be performed with significantly reduced compute and GPU hours by utilizing fewer but reusable training runs. Our code is available at https://github.com/epfml/schedules-and-scaling.

BaCaDI: Bayesian Causal Discovery with Unknown Interventions

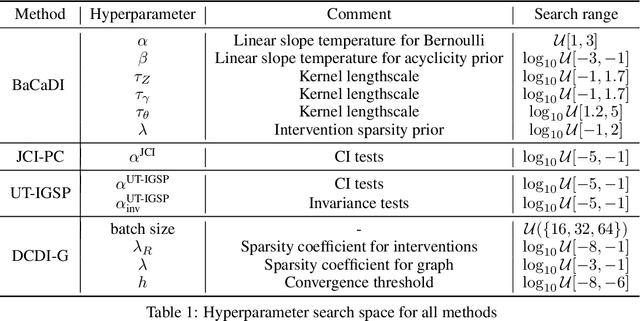
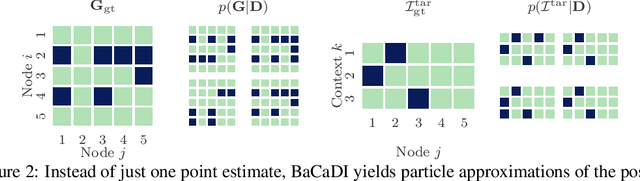
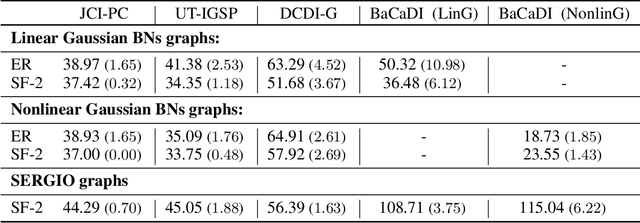
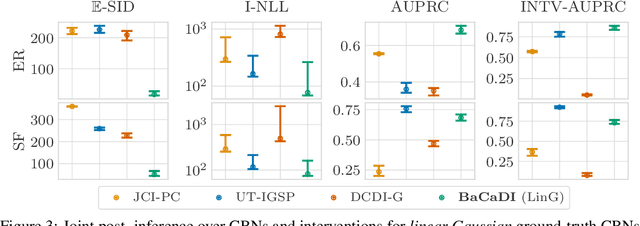
Learning causal structures from observation and experimentation is a central task in many domains. For example, in biology, recent advances allow us to obtain single-cell expression data under multiple interventions such as drugs or gene knockouts. However, a key challenge is that often the targets of the interventions are uncertain or unknown. Thus, standard causal discovery methods can no longer be used. To fill this gap, we propose a Bayesian framework (BaCaDI) for discovering the causal structure that underlies data generated under various unknown experimental/interventional conditions. BaCaDI is fully differentiable and operates in the continuous space of latent probabilistic representations of both causal structures and interventions. This enables us to approximate complex posteriors via gradient-based variational inference and to reason about the epistemic uncertainty in the predicted structure. In experiments on synthetic causal discovery tasks and simulated gene-expression data, BaCaDI outperforms related methods in identifying causal structures and intervention targets. Finally, we demonstrate that, thanks to its rigorous Bayesian approach, our method provides well-calibrated uncertainty estimates.