Learning Fast Magnetic Resonance Imaging

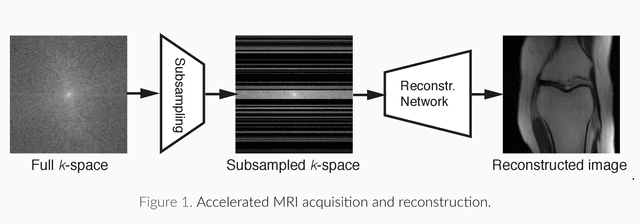
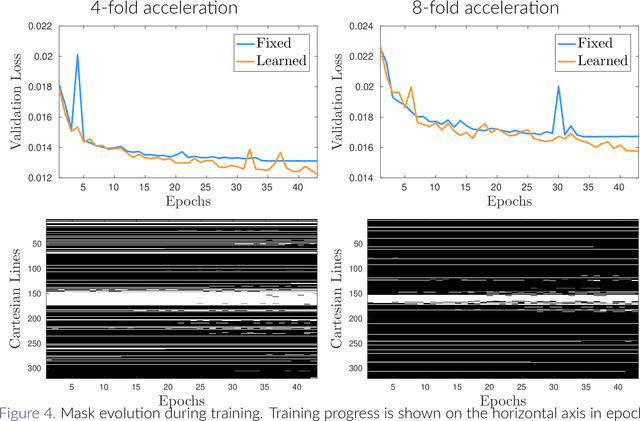
Magnetic Resonance Imaging (MRI) is considered today the golden-standard modality for soft tissues. The long acquisition times, however, make it more prone to motion artifacts as well as contribute to the relatively high costs of this examination. Over the years, multiple studies concentrated on designing reduced measurement schemes and image reconstruction schemes for MRI, however, these problems have been so far addressed separately. On the other hand, recent works in optical computational imaging have demonstrated growing success of the simultaneous learning-based design of the acquisition and reconstruction schemes manifesting significant improvement in the reconstruction quality with a constrained time budget. Inspired by these successes, in this work, we propose to learn accelerated MR acquisition schemes (in the form of Cartesian trajectories) jointly with the image reconstruction operator. To this end, we propose an algorithm for training the combined acquisition-reconstruction pipeline end-to-end in a differentiable way. We demonstrate the significance of using the learned Cartesian trajectories at different speed up rates.

Learning beamforming in ultrasound imaging

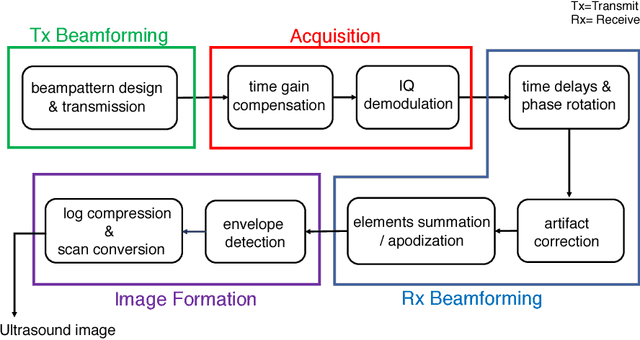
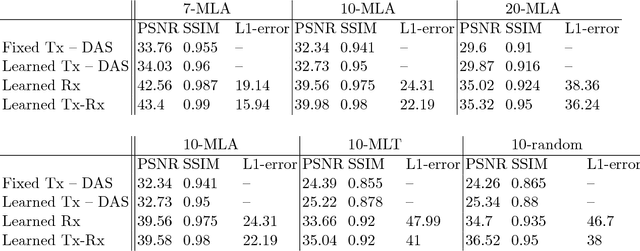
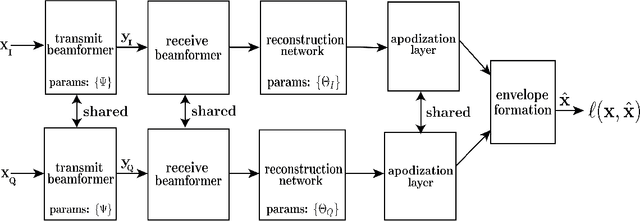
Medical ultrasound (US) is a widespread imaging modality owing its popularity to cost efficiency, portability, speed, and lack of harmful ionizing radiation. In this paper, we demonstrate that replacing the traditional ultrasound processing pipeline with a data-driven, learnable counterpart leads to significant improvement in image quality. Moreover, we demonstrate that greater improvement can be achieved through a learning-based design of the transmitted beam patterns simultaneously with learning an image reconstruction pipeline. We evaluate our method on an in-vivo first-harmonic cardiac ultrasound dataset acquired from volunteers and demonstrate the significance of the learned pipeline and transmit beam patterns on the image quality when compared to standard transmit and receive beamformers used in high frame-rate US imaging. We believe that the presented methodology provides a fundamentally different perspective on the classical problem of ultrasound beam pattern design.

Self-supervised Learning of Dense Shape Correspondence

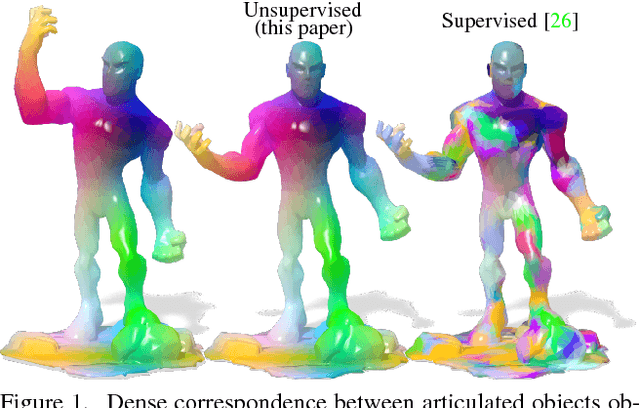
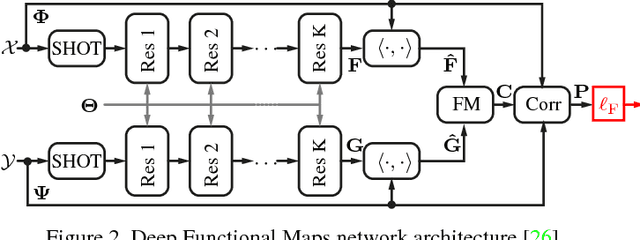
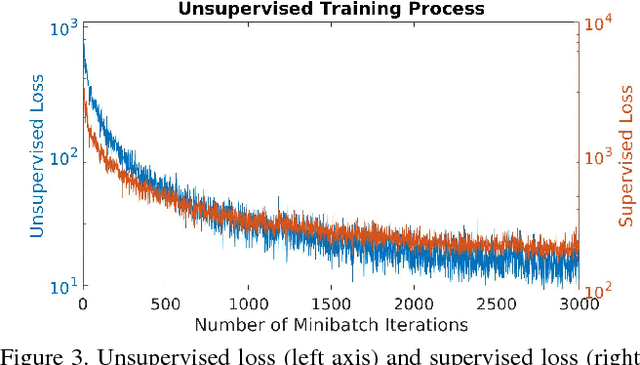
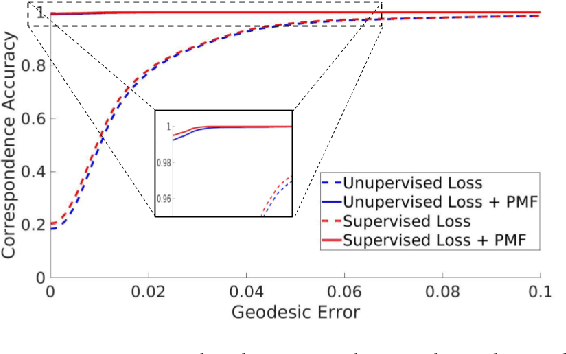
We introduce the first completely unsupervised correspondence learning approach for deformable 3D shapes. Key to our model is the understanding that natural deformations (such as changes in pose) approximately preserve the metric structure of the surface, yielding a natural criterion to drive the learning process toward distortion-minimizing predictions. On this basis, we overcome the need for annotated data and replace it by a purely geometric criterion. The resulting learning model is class-agnostic, and is able to leverage any type of deformable geometric data for the training phase. In contrast to existing supervised approaches which specialize on the class seen at training time, we demonstrate stronger generalization as well as applicability to a variety of challenging settings. We showcase our method on a wide selection of correspondence benchmarks, where we outperform other methods in terms of accuracy, generalization, and efficiency.

SGR: Self-Supervised Spectral Graph Representation Learning

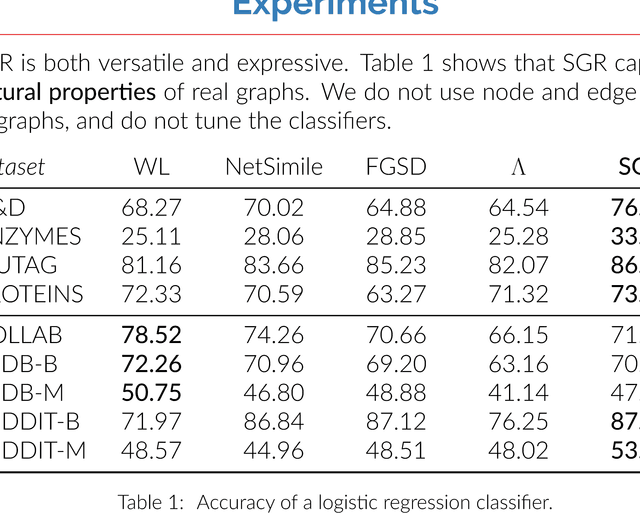
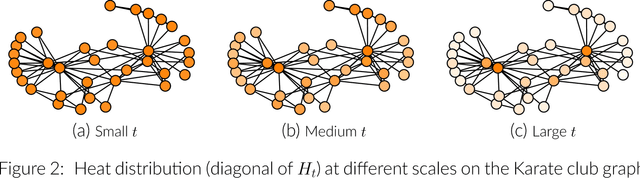
Representing a graph as a vector is a challenging task; ideally, the representation should be easily computable and conducive to efficient comparisons among graphs, tailored to the particular data and analytical task at hand. Unfortunately, a "one-size-fits-all" solution is unattainable, as different analytical tasks may require different attention to global or local graph features. We develop SGR, the first, to our knowledge, method for learning graph representations in a self-supervised manner. Grounded on spectral graph analysis, SGR seamlessly combines all aforementioned desirable properties. In extensive experiments, we show how our approach works on large graph collections, facilitates self-supervised representation learning across a variety of application domains, and performs competitively to state-of-the-art methods without re-training.

ForestHash: Semantic Hashing With Shallow Random Forests and Tiny Convolutional Networks

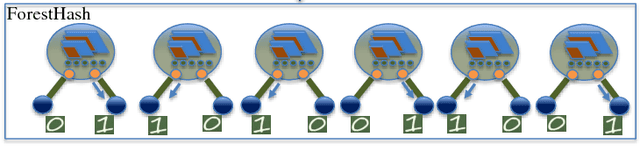
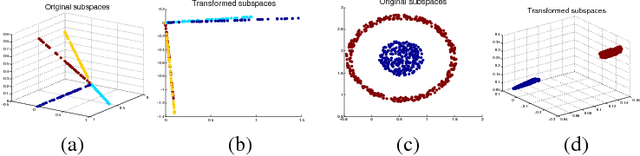
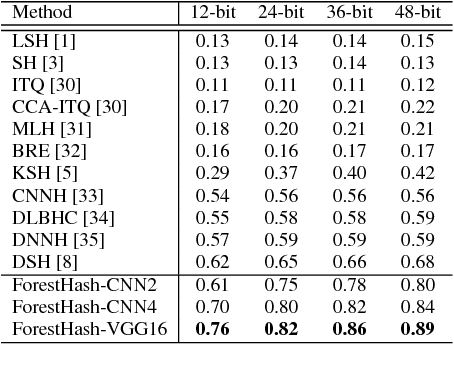
Hash codes are efficient data representations for coping with the ever growing amounts of data. In this paper, we introduce a random forest semantic hashing scheme that embeds tiny convolutional neural networks (CNN) into shallow random forests, with near-optimal information-theoretic code aggregation among trees. We start with a simple hashing scheme, where random trees in a forest act as hashing functions by setting `1' for the visited tree leaf, and `0' for the rest. We show that traditional random forests fail to generate hashes that preserve the underlying similarity between the trees, rendering the random forests approach to hashing challenging. To address this, we propose to first randomly group arriving classes at each tree split node into two groups, obtaining a significantly simplified two-class classification problem, which can be handled using a light-weight CNN weak learner. Such random class grouping scheme enables code uniqueness by enforcing each class to share its code with different classes in different trees. A non-conventional low-rank loss is further adopted for the CNN weak learners to encourage code consistency by minimizing intra-class variations and maximizing inter-class distance for the two random class groups. Finally, we introduce an information-theoretic approach for aggregating codes of individual trees into a single hash code, producing a near-optimal unique hash for each class. The proposed approach significantly outperforms state-of-the-art hashing methods for image retrieval tasks on large-scale public datasets, while performing at the level of other state-of-the-art image classification techniques while utilizing a more compact and efficient scalable representation. This work proposes a principled and robust procedure to train and deploy in parallel an ensemble of light-weight CNNs, instead of simply going deeper.

Deformable Shape Completion with Graph Convolutional Autoencoders

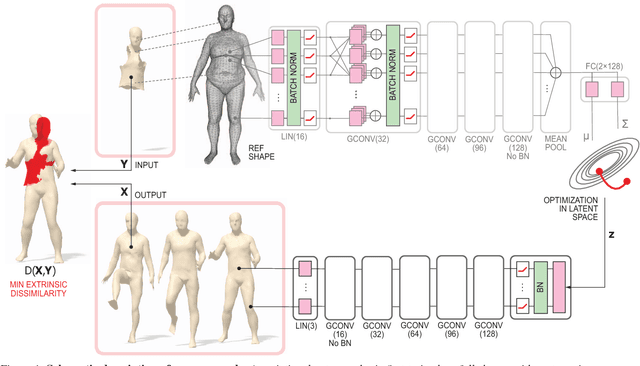
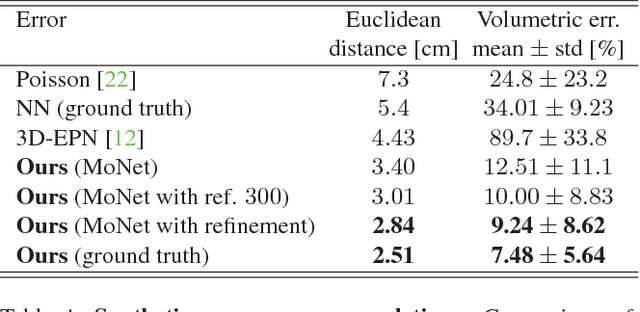
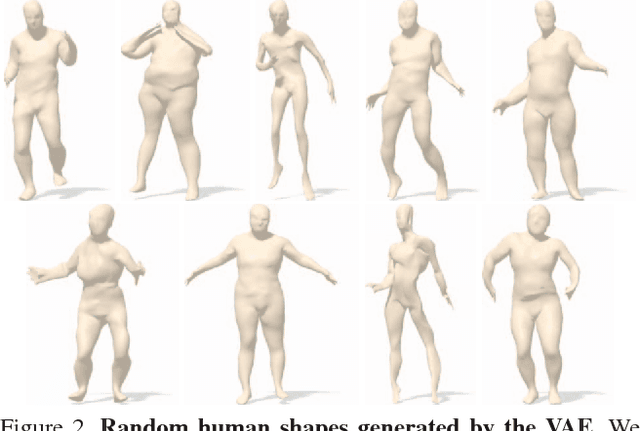
The availability of affordable and portable depth sensors has made scanning objects and people simpler than ever. However, dealing with occlusions and missing parts is still a significant challenge. The problem of reconstructing a (possibly non-rigidly moving) 3D object from a single or multiple partial scans has received increasing attention in recent years. In this work, we propose a novel learning-based method for the completion of partial shapes. Unlike the majority of existing approaches, our method focuses on objects that can undergo non-rigid deformations. The core of our method is a variational autoencoder with graph convolutional operations that learns a latent space for complete realistic shapes. At inference, we optimize to find the representation in this latent space that best fits the generated shape to the known partial input. The completed shape exhibits a realistic appearance on the unknown part. We show promising results towards the completion of synthetic and real scans of human body and face meshes exhibiting different styles of articulation and partiality.

Efficient Deformable Shape Correspondence via Kernel Matching

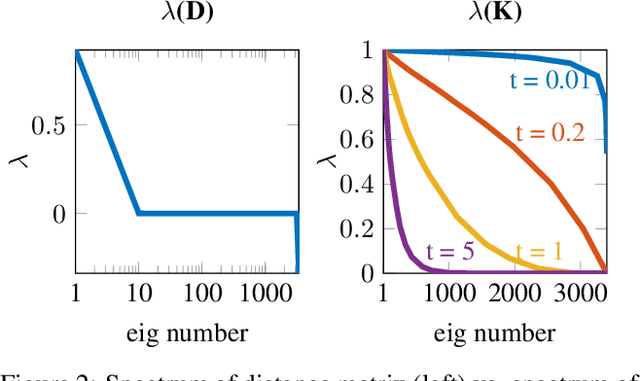
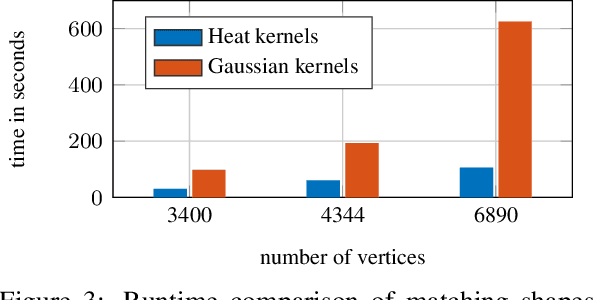
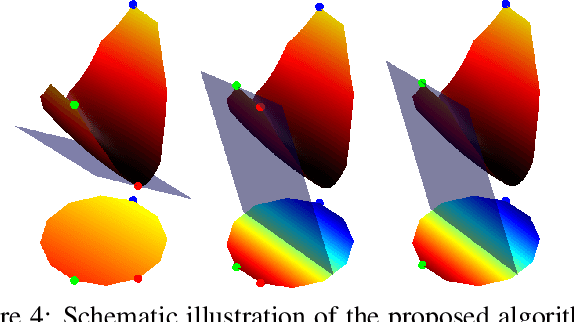
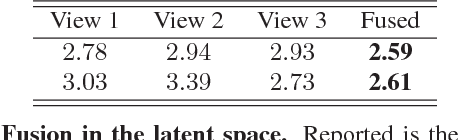
We present a method to match three dimensional shapes under non-isometric deformations, topology changes and partiality. We formulate the problem as matching between a set of pair-wise and point-wise descriptors, imposing a continuity prior on the mapping, and propose a projected descent optimization procedure inspired by difference of convex functions (DC) programming. Surprisingly, in spite of the highly non-convex nature of the resulting quadratic assignment problem, our method converges to a semantically meaningful and continuous mapping in most of our experiments, and scales well. We provide preliminary theoretical analysis and several interpretations of the method.

Hamiltonian operator for spectral shape analysis

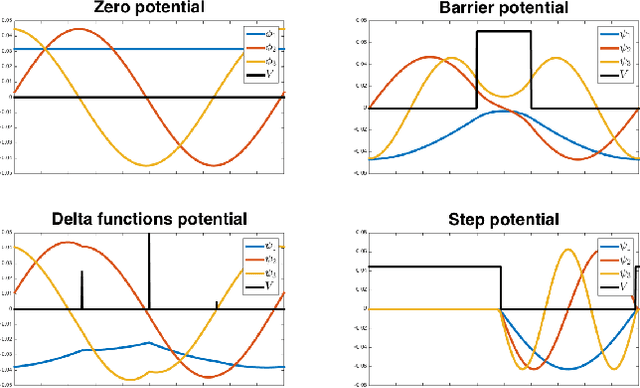
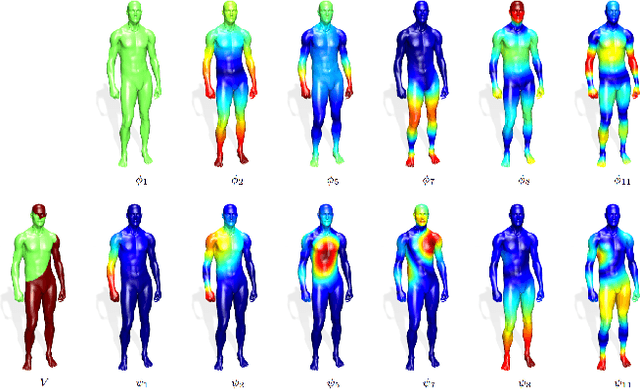
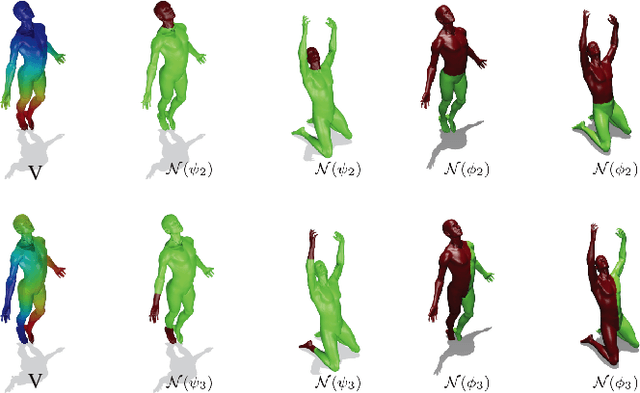
Many shape analysis methods treat the geometry of an object as a metric space that can be captured by the Laplace-Beltrami operator. In this paper, we propose to adapt the classical Hamiltonian operator from quantum mechanics to the field of shape analysis. To this end we study the addition of a potential function to the Laplacian as a generator for dual spaces in which shape processing is performed. We present a general optimization approach for solving variational problems involving the basis defined by the Hamiltonian using perturbation theory for its eigenvectors. The suggested operator is shown to produce better functional spaces to operate with, as demonstrated on different shape analysis tasks.

Product Manifold Filter: Non-Rigid Shape Correspondence via Kernel Density Estimation in the Product Space

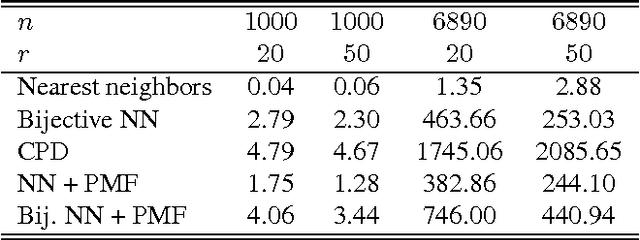
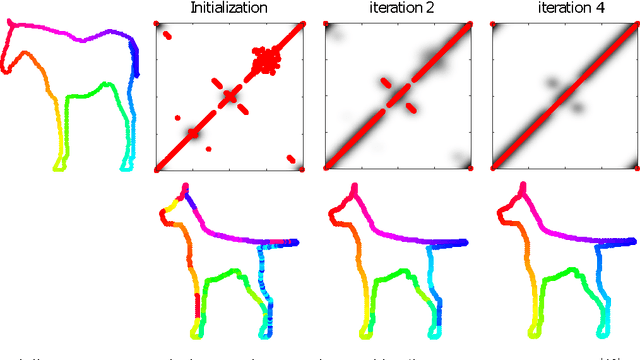
Many algorithms for the computation of correspondences between deformable shapes rely on some variant of nearest neighbor matching in a descriptor space. Such are, for example, various point-wise correspondence recovery algorithms used as a post-processing stage in the functional correspondence framework. Such frequently used techniques implicitly make restrictive assumptions (e.g., near-isometry) on the considered shapes and in practice suffer from lack of accuracy and result in poor surjectivity. We propose an alternative recovery technique capable of guaranteeing a bijective correspondence and producing significantly higher accuracy and smoothness. Unlike other methods our approach does not depend on the assumption that the analyzed shapes are isometric. We derive the proposed method from the statistical framework of kernel density estimation and demonstrate its performance on several challenging deformable 3D shape matching datasets.

Cloud Dictionary: Sparse Coding and Modeling for Point Clouds

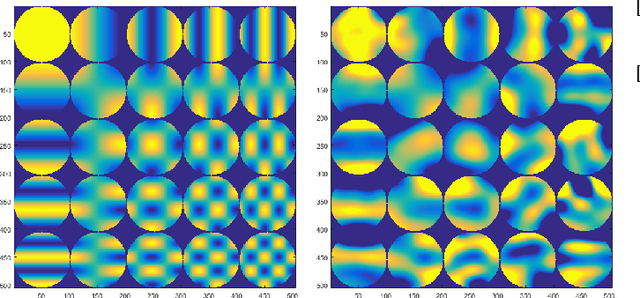
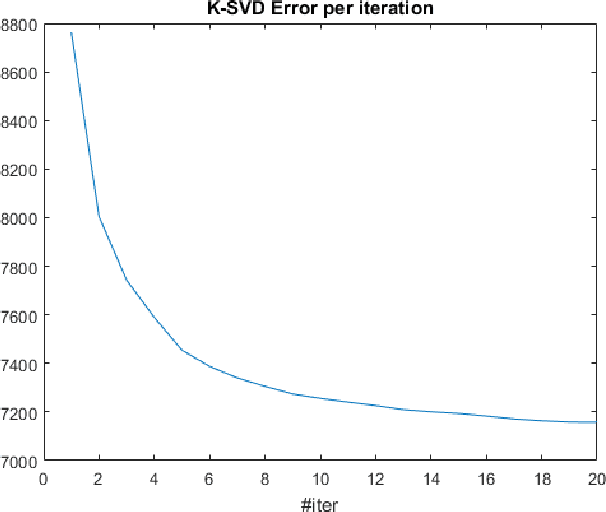
With the development of range sensors such as LIDAR and time-of-flight cameras, 3D point cloud scans have become ubiquitous in computer vision applications, the most prominent ones being gesture recognition and autonomous driving. Parsimony-based algorithms have shown great success on images and videos where data points are sampled on a regular Cartesian grid. We propose an adaptation of these techniques to irregularly sampled signals by using continuous dictionaries. We present an example application in the form of point cloud denoising.