Hamiltonian operator for spectral shape analysis

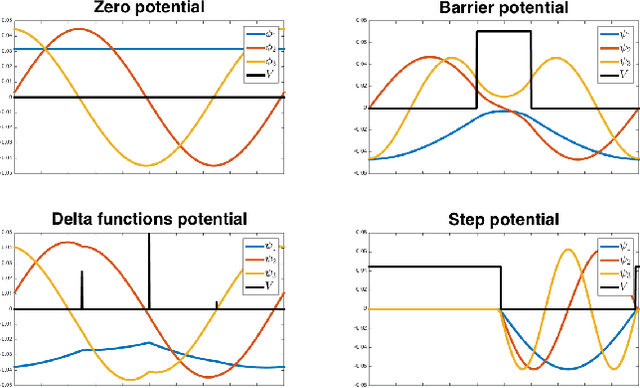
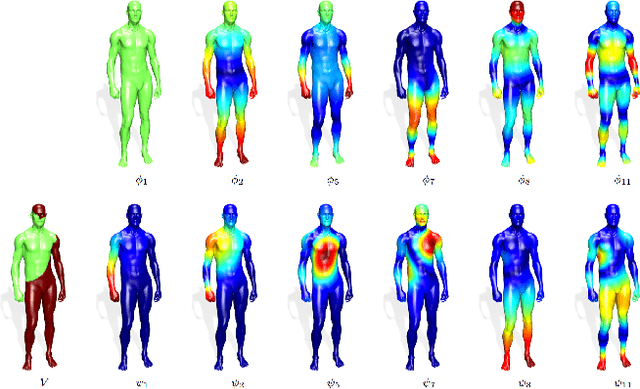
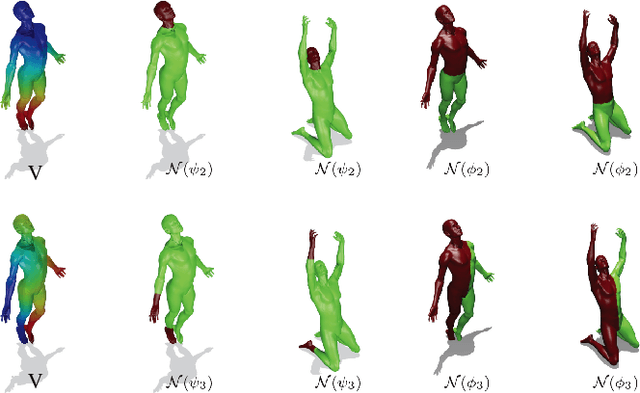
Many shape analysis methods treat the geometry of an object as a metric space that can be captured by the Laplace-Beltrami operator. In this paper, we propose to adapt the classical Hamiltonian operator from quantum mechanics to the field of shape analysis. To this end we study the addition of a potential function to the Laplacian as a generator for dual spaces in which shape processing is performed. We present a general optimization approach for solving variational problems involving the basis defined by the Hamiltonian using perturbation theory for its eigenvectors. The suggested operator is shown to produce better functional spaces to operate with, as demonstrated on different shape analysis tasks.

On Nonrigid Shape Similarity and Correspondence

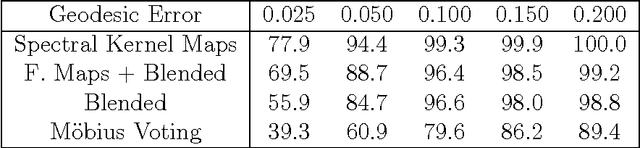
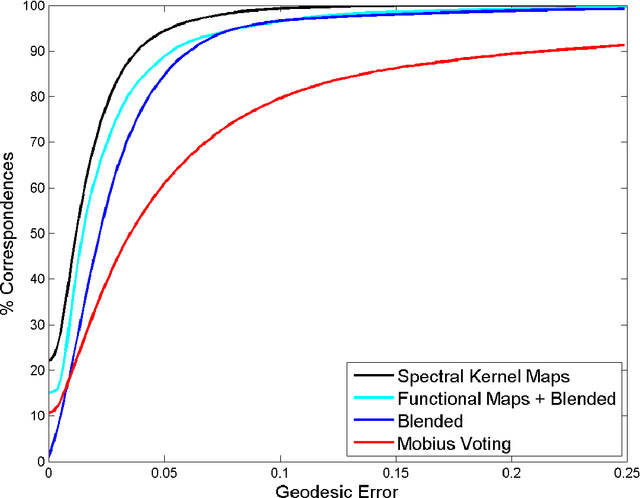
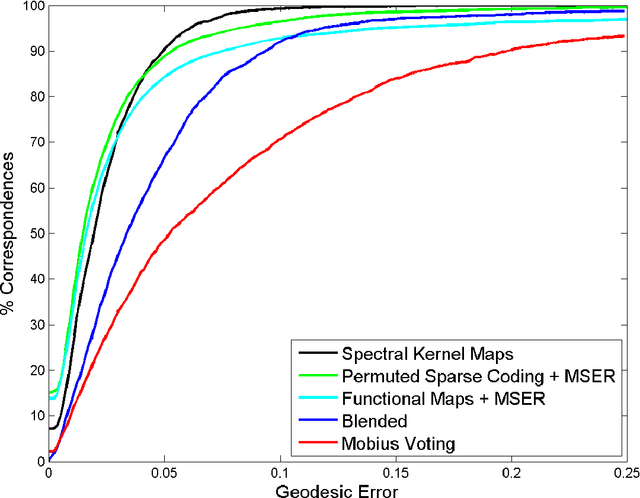
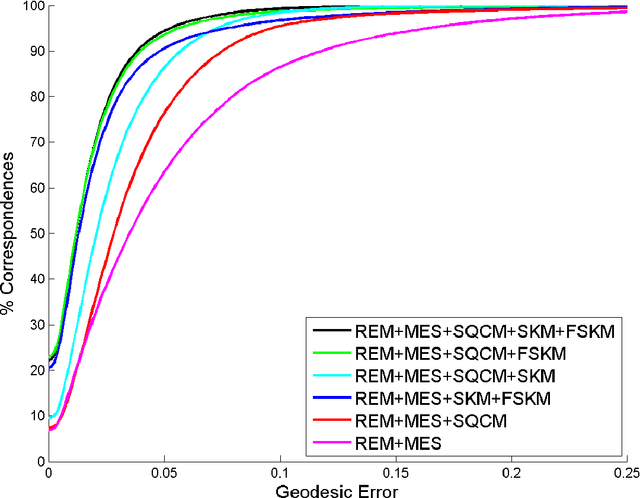
An important operation in geometry processing is finding the correspondences between pairs of shapes. The Gromov-Hausdorff distance, a measure of dissimilarity between metric spaces, has been found to be highly useful for nonrigid shape comparison. Here, we explore the applicability of related shape similarity measures to the problem of shape correspondence, adopting spectral type distances. We propose to evaluate the spectral kernel distance, the spectral embedding distance and the novel spectral quasi-conformal distance, comparing the manifolds from different viewpoints. By matching the shapes in the spectral domain, important attributes of surface structure are being aligned. For the purpose of testing our ideas, we introduce a fully automatic framework for finding intrinsic correspondence between two shapes. The proposed method achieves state-of-the-art results on the Princeton isometric shape matching protocol applied, as usual, to the TOSCA and SCAPE benchmarks.