Alessandro Lazaric
INRIA Lille - Nord Europe
A Structured Prediction Approach for Generalization in Cooperative Multi-Agent Reinforcement Learning
Oct 19, 2019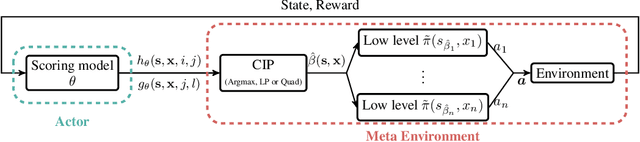
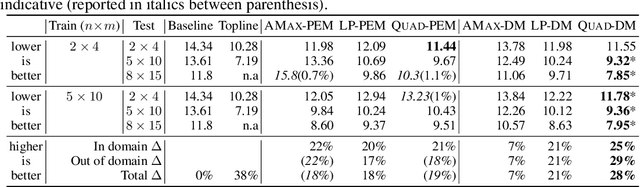
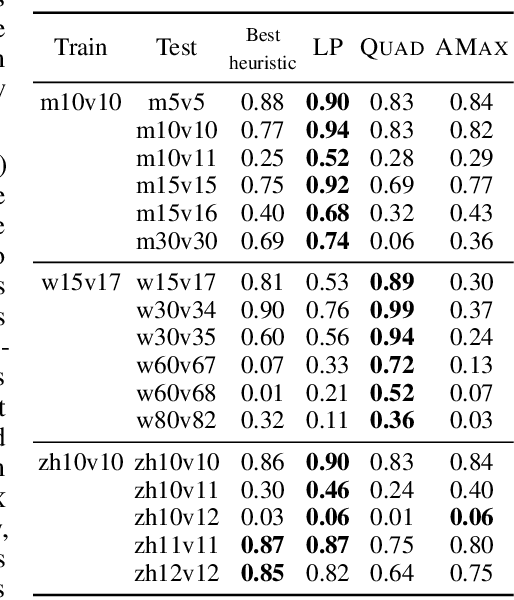
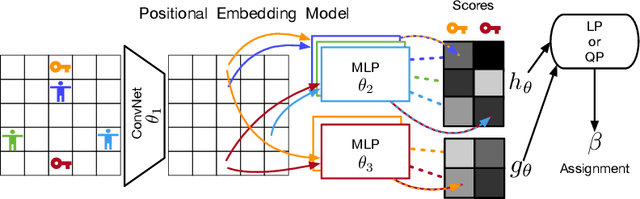
Abstract:Effective coordination is crucial to solve multi-agent collaborative (MAC) problems. While centralized reinforcement learning methods can optimally solve small MAC instances, they do not scale to large problems and they fail to generalize to scenarios different from those seen during training. In this paper, we consider MAC problems with some intrinsic notion of locality (e.g., geographic proximity) such that interactions between agents and tasks are locally limited. By leveraging this property, we introduce a novel structured prediction approach to assign agents to tasks. At each step, the assignment is obtained by solving a centralized optimization problem (the inference procedure) whose objective function is parameterized by a learned scoring model. We propose different combinations of inference procedures and scoring models able to represent coordination patterns of increasing complexity. The resulting assignment policy can be efficiently learned on small problem instances and readily reused in problems with more agents and tasks (i.e., zero-shot generalization). We report experimental results on a toy search and rescue problem and on several target selection scenarios in StarCraft: Brood War, in which our model significantly outperforms strong rule-based baselines on instances with 5 times more agents and tasks than those seen during training.
Word-order biases in deep-agent emergent communication
Jun 14, 2019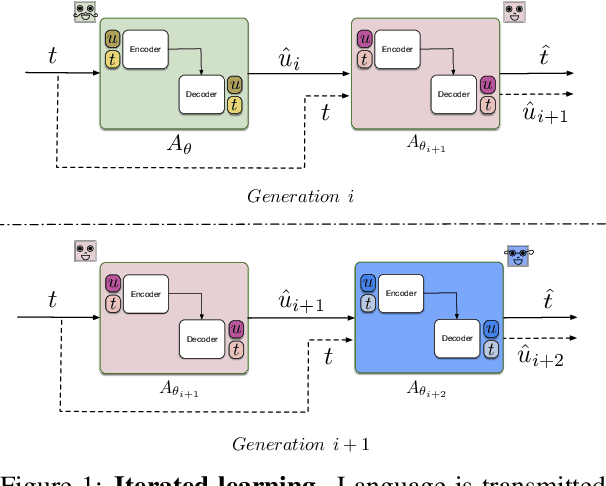
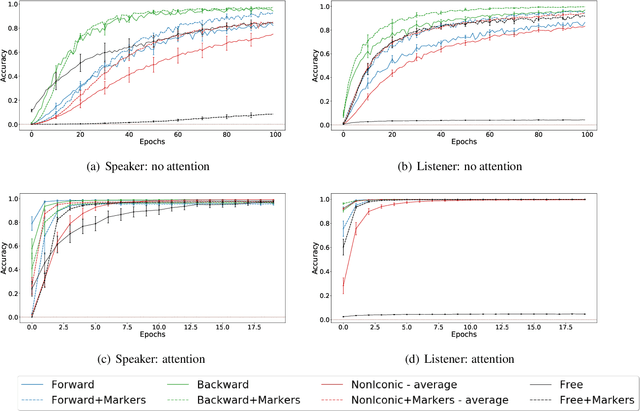
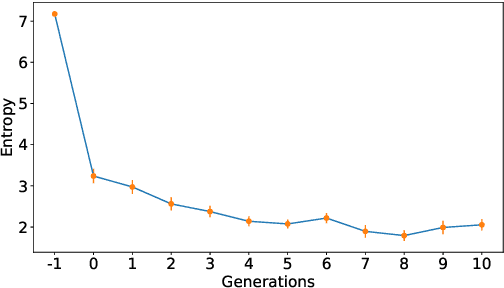
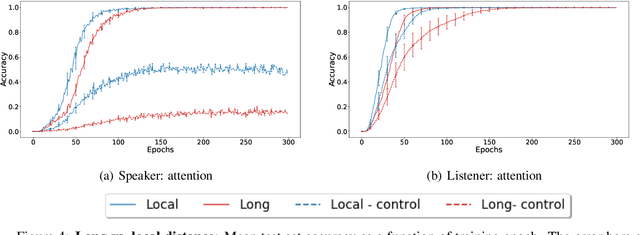
Abstract:Sequence-processing neural networks led to remarkable progress on many NLP tasks. As a consequence, there has been increasing interest in understanding to what extent they process language as humans do. We aim here to uncover which biases such models display with respect to "natural" word-order constraints. We train models to communicate about paths in a simple gridworld, using miniature languages that reflect or violate various natural language trends, such as the tendency to avoid redundancy or to minimize long-distance dependencies. We study how the controlled characteristics of our miniature languages affect individual learning and their stability across multiple network generations. The results draw a mixed picture. On the one hand, neural networks show a strong tendency to avoid long-distance dependencies. On the other hand, there is no clear preference for the efficient, non-redundant encoding of information that is widely attested in natural language. We thus suggest inoculating a notion of "effort" into neural networks, as a possible way to make their linguistic behavior more human-like.
Gaussian Process Optimization with Adaptive Sketching: Scalable and No Regret
Mar 13, 2019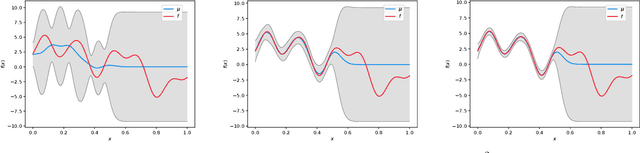
Abstract:Gaussian processes (GP) are a popular Bayesian approach for the optimization of black-box functions. Despite their effectiveness in simple problems, GP-based algorithms hardly scale to complex high-dimensional functions, as their per-iteration time and space cost is at least quadratic in the number of dimensions $d$ and iterations $t$. Given a set of $A$ alternative to choose from, the overall runtime $O(t^3A)$ quickly becomes prohibitive. In this paper, we introduce BKB (budgeted kernelized bandit), a novel approximate GP algorithm for optimization under bandit feedback that achieves near-optimal regret (and hence near-optimal convergence rate) with near-constant per-iteration complexity and no assumption on the input space or covariance of the GP. Combining a kernelized linear bandit algorithm (GP-UCB) with randomized matrix sketching technique (i.e., leverage score sampling), we prove that selecting inducing points based on their posterior variance gives an accurate low-rank approximation of the GP, preserving variance estimates and confidence intervals. As a consequence, BKB does not suffer from variance starvation, an important problem faced by many previous sparse GP approximations. Moreover, we show that our procedure selects at most $\tilde{O}(d_{eff})$ points, where $d_{eff}$ is the effective dimension of the explored space, which is typically much smaller than both $d$ and $t$. This greatly reduces the dimensionality of the problem, thus leading to a $O(TAd_{eff}^2)$ runtime and $O(A d_{eff})$ space complexity.
Active Exploration in Markov Decision Processes
Feb 28, 2019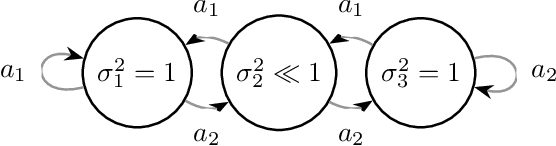
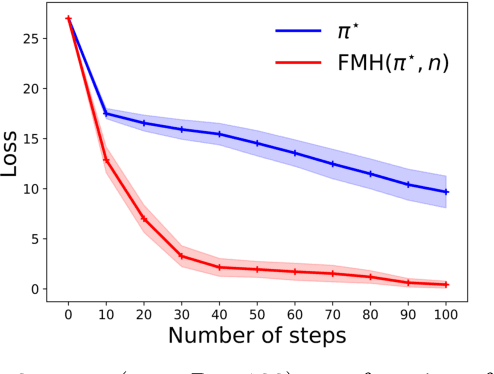
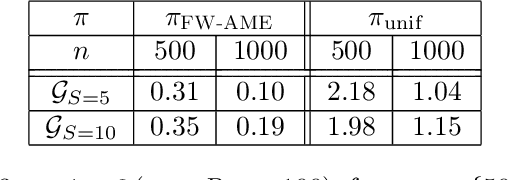
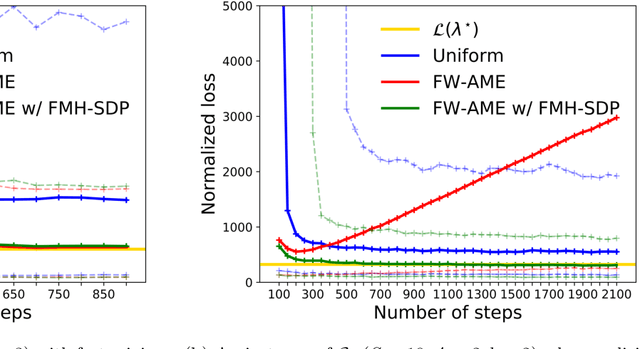
Abstract:We introduce the active exploration problem in Markov decision processes (MDPs). Each state of the MDP is characterized by a random value and the learner should gather samples to estimate the mean value of each state as accurately as possible. Similarly to active exploration in multi-armed bandit (MAB), states may have different levels of noise, so that the higher the noise, the more samples are needed. As the noise level is initially unknown, we need to trade off the exploration of the environment to estimate the noise and the exploitation of these estimates to compute a policy maximizing the accuracy of the mean predictions. We introduce a novel learning algorithm to solve this problem showing that active exploration in MDPs may be significantly more difficult than in MAB. We also derive a heuristic procedure to mitigate the negative effect of slowly mixing policies. Finally, we validate our findings on simple numerical simulations.
Exploration Bonus for Regret Minimization in Undiscounted Discrete and Continuous Markov Decision Processes
Dec 11, 2018Abstract:We introduce and analyse two algorithms for exploration-exploitation in discrete and continuous Markov Decision Processes (MDPs) based on exploration bonuses. SCAL$^+$ is a variant of SCAL (Fruit et al., 2018) that performs efficient exploration-exploitation in any unknown weakly-communicating MDP for which an upper bound C on the span of the optimal bias function is known. For an MDP with $S$ states, $A$ actions and $\Gamma \leq S$ possible next states, we prove that SCAL$^+$ achieves the same theoretical guarantees as SCAL (i.e., a high probability regret bound of $\widetilde{O}(C\sqrt{\Gamma SAT})$), with a much smaller computational complexity. Similarly, C-SCAL$^+$ exploits an exploration bonus to achieve sublinear regret in any undiscounted MDP with continuous state space. We show that C-SCAL$^+$ achieves the same regret bound as UCCRL (Ortner and Ryabko, 2012) while being the first implementable algorithm with regret guarantees in this setting. While optimistic algorithms such as UCRL, SCAL or UCCRL maintain a high-confidence set of plausible MDPs around the true unknown MDP, SCAL$^+$ and C-SCAL$^+$ leverage on an exploration bonus to directly plan on the empirically estimated MDP, thus being more computationally efficient.
Rotting bandits are no harder than stochastic ones
Nov 27, 2018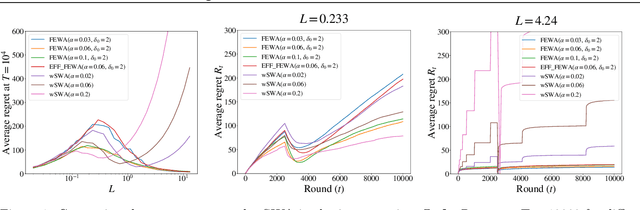
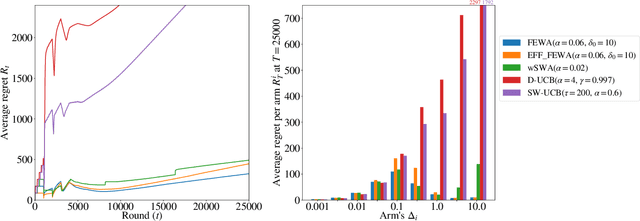
Abstract:In bandits, arms' distributions are stationary. This is often violated in practice, where rewards change over time. In applications as recommendation systems, online advertising, and crowdsourcing, the changes may be triggered by the pulls, so that the arms' rewards change as a function of the number of pulls. In this paper, we consider the specific case of non-parametric rotting bandits, where the expected reward of an arm may decrease every time it is pulled. We introduce the filtering on expanding window average (FEWA) algorithm that at each round constructs moving averages of increasing windows to identify arms that are more likely to return high rewards when pulled once more. We prove that, without any knowledge on the decreasing behavior of the arms, FEWA achieves similar anytime problem-dependent, $\widetilde{\mathcal{O}}(\log{(KT)}),$ and problem-independent, $\widetilde{\mathcal{O}}(\sqrt{KT})$, regret bounds of near-optimal stochastic algorithms as UCB1 of Auer et al. (2002a). This result substantially improves the prior result of Levine et al. (2017) which needed knowledge of the horizon and decaying parameters to achieve problem-independent bound of only $\widetilde{\mathcal{O}}(K^{1/3}T^{2/3})$. Finally, we report simulations confirming the theoretical improvements of FEWA.
Efficient Bias-Span-Constrained Exploration-Exploitation in Reinforcement Learning
Jul 06, 2018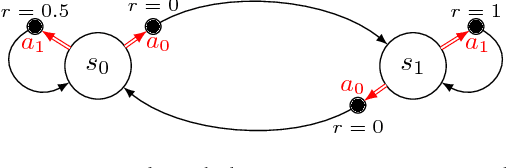
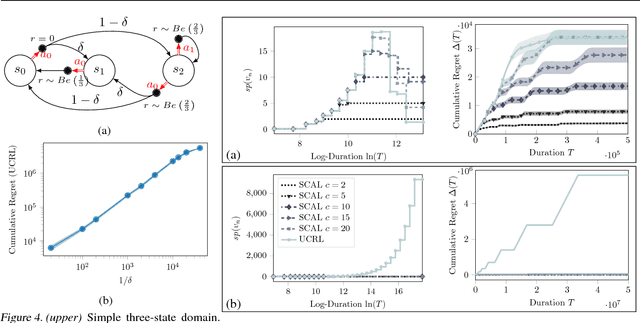
Abstract:We introduce SCAL, an algorithm designed to perform efficient exploration-exploitation in any unknown weakly-communicating Markov decision process (MDP) for which an upper bound $c$ on the span of the optimal bias function is known. For an MDP with $S$ states, $A$ actions and $\Gamma \leq S$ possible next states, we prove a regret bound of $\widetilde{O}(c\sqrt{\Gamma SAT})$, which significantly improves over existing algorithms (e.g., UCRL and PSRL), whose regret scales linearly with the MDP diameter $D$. In fact, the optimal bias span is finite and often much smaller than $D$ (e.g., $D=\infty$ in non-communicating MDPs). A similar result was originally derived by Bartlett and Tewari (2009) for REGAL.C, for which no tractable algorithm is available. In this paper, we relax the optimization problem at the core of REGAL.C, we carefully analyze its properties, and we provide the first computationally efficient algorithm to solve it. Finally, we report numerical simulations supporting our theoretical findings and showing how SCAL significantly outperforms UCRL in MDPs with large diameter and small span.
Near Optimal Exploration-Exploitation in Non-Communicating Markov Decision Processes
Jul 06, 2018
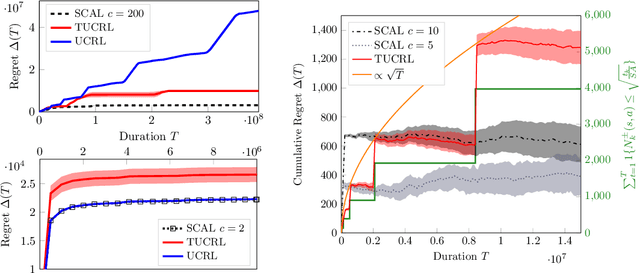
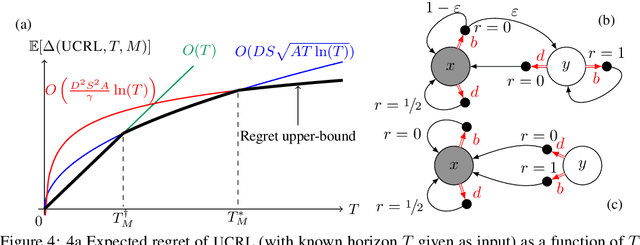
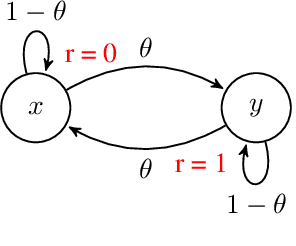
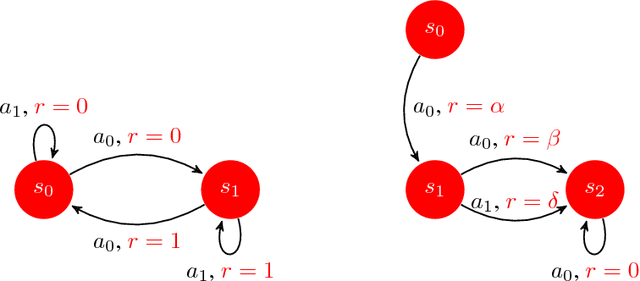
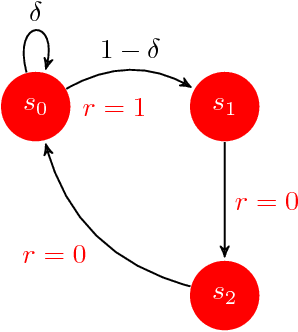
Abstract:While designing the state space of an MDP, it is common to include states that are transient or not reachable by any policy (e.g., in mountain car, the product space of speed and position contains configurations that are not physically reachable). This leads to defining weakly-communicating or multi-chain MDPs. In this paper, we introduce \tucrl, the first algorithm able to perform efficient exploration-exploitation in any finite Markov Decision Process (MDP) without requiring any form of prior knowledge. In particular, for any MDP with $S^{\texttt{C}}$ communicating states, $A$ actions and $\Gamma^{\texttt{C}} \leq S^{\texttt{C}}$ possible communicating next states, we derive a $\widetilde{O}(D^{\texttt{C}} \sqrt{\Gamma^{\texttt{C}} S^{\texttt{C}} AT})$ regret bound, where $D^{\texttt{C}}$ is the diameter (i.e., the longest shortest path) of the communicating part of the MDP. This is in contrast with optimistic algorithms (e.g., UCRL, Optimistic PSRL) that suffer linear regret in weakly-communicating MDPs, as well as posterior sampling or regularised algorithms (e.g., REGAL), which require prior knowledge on the bias span of the optimal policy to bias the exploration to achieve sub-linear regret. We also prove that in weakly-communicating MDPs, no algorithm can ever achieve a logarithmic growth of the regret without first suffering a linear regret for a number of steps that is exponential in the parameters of the MDP. Finally, we report numerical simulations supporting our theoretical findings and showing how TUCRL overcomes the limitations of the state-of-the-art.
Reinforcement Learning in Rich-Observation MDPs using Spectral Methods
Jun 19, 2018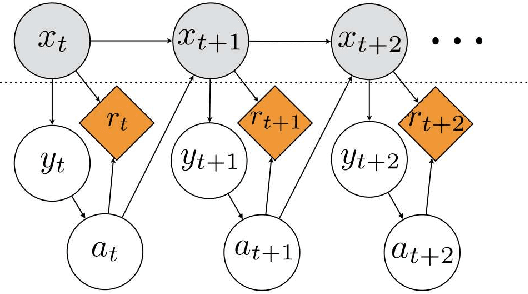
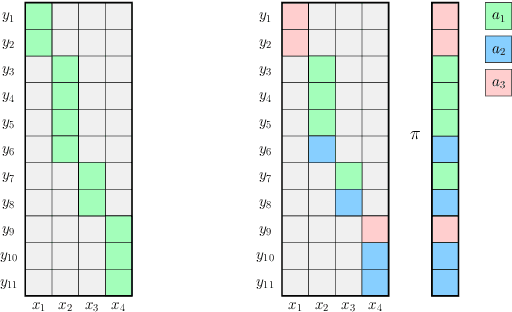
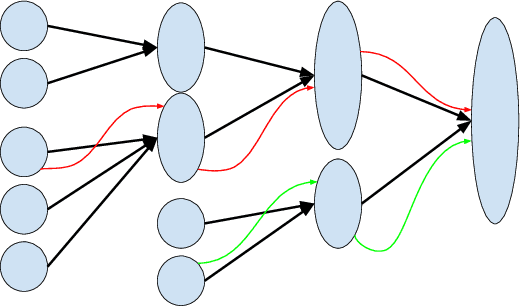
Abstract:Reinforcement learning (RL) in Markov decision processes (MDPs) with large state spaces is a challenging problem. The performance of standard RL algorithms degrades drastically with the dimensionality of state space. However, in practice, these large MDPs typically incorporate a latent or hidden low-dimensional structure. In this paper, we study the setting of rich-observation Markov decision processes (ROMDP), where there are a small number of hidden states which possess an injective mapping to the observation states. In other words, every observation state is generated through a single hidden state, and this mapping is unknown a priori. We introduce a spectral decomposition method that consistently learns this mapping, and more importantly, achieves it with low regret. The estimated mapping is integrated into an optimistic RL algorithm (UCRL), which operates on the estimated hidden space. We derive finite-time regret bounds for our algorithm with a weak dependence on the dimensionality of the observed space. In fact, our algorithm asymptotically achieves the same average regret as the oracle UCRL algorithm, which has the knowledge of the mapping from hidden to observed spaces. Thus, we derive an efficient spectral RL algorithm for ROMDPs.
Distributed Adaptive Sampling for Kernel Matrix Approximation
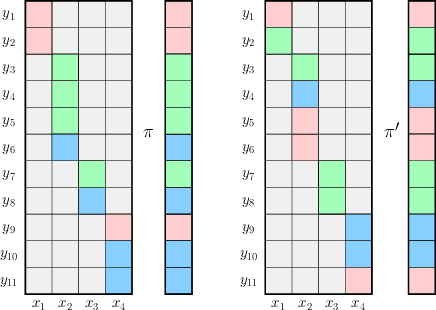
Mar 27, 2018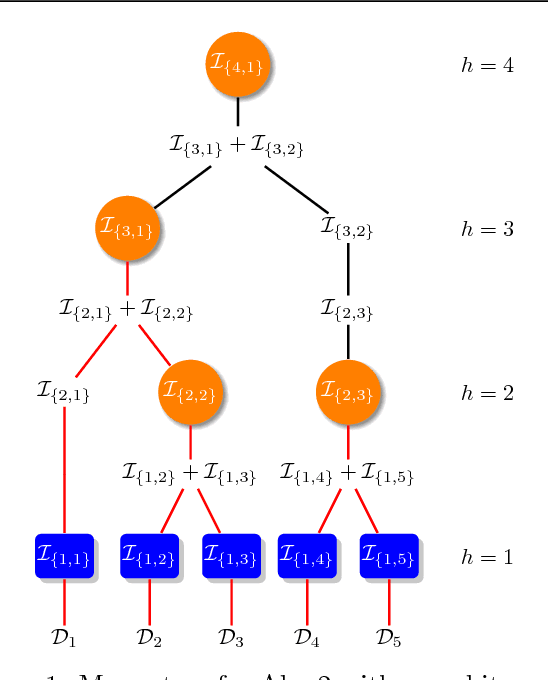

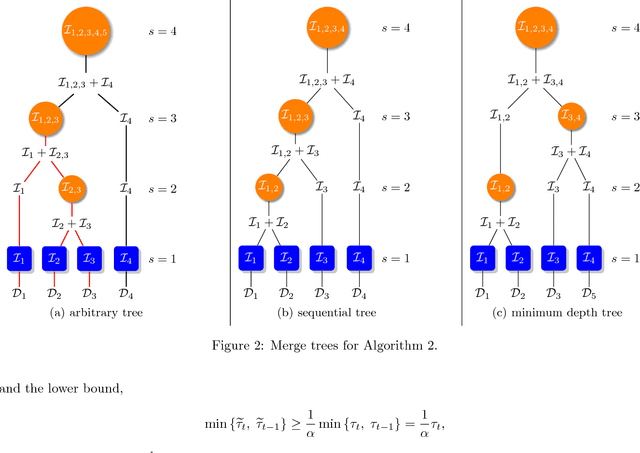
Abstract:Most kernel-based methods, such as kernel or Gaussian process regression, kernel PCA, ICA, or $k$-means clustering, do not scale to large datasets, because constructing and storing the kernel matrix $\mathbf{K}_n$ requires at least $\mathcal{O}(n^2)$ time and space for $n$ samples. Recent works show that sampling points with replacement according to their ridge leverage scores (RLS) generates small dictionaries of relevant points with strong spectral approximation guarantees for $\mathbf{K}_n$. The drawback of RLS-based methods is that computing exact RLS requires constructing and storing the whole kernel matrix. In this paper, we introduce SQUEAK, a new algorithm for kernel approximation based on RLS sampling that sequentially processes the dataset, storing a dictionary which creates accurate kernel matrix approximations with a number of points that only depends on the effective dimension $d_{eff}(\gamma)$ of the dataset. Moreover since all the RLS estimations are efficiently performed using only the small dictionary, SQUEAK is the first RLS sampling algorithm that never constructs the whole matrix $\mathbf{K}_n$, runs in linear time $\widetilde{\mathcal{O}}(nd_{eff}(\gamma)^3)$ w.r.t. $n$, and requires only a single pass over the dataset. We also propose a parallel and distributed version of SQUEAK that linearly scales across multiple machines, achieving similar accuracy in as little as $\widetilde{\mathcal{O}}(\log(n)d_{eff}(\gamma)^3)$ time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge