Rotting bandits are no harder than stochastic ones

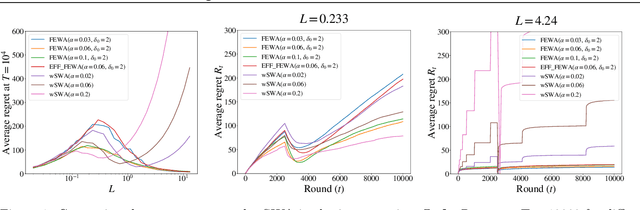
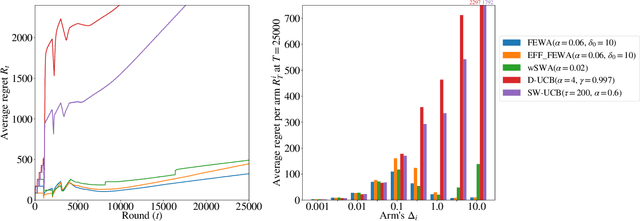
In bandits, arms' distributions are stationary. This is often violated in practice, where rewards change over time. In applications as recommendation systems, online advertising, and crowdsourcing, the changes may be triggered by the pulls, so that the arms' rewards change as a function of the number of pulls. In this paper, we consider the specific case of non-parametric rotting bandits, where the expected reward of an arm may decrease every time it is pulled. We introduce the filtering on expanding window average (FEWA) algorithm that at each round constructs moving averages of increasing windows to identify arms that are more likely to return high rewards when pulled once more. We prove that, without any knowledge on the decreasing behavior of the arms, FEWA achieves similar anytime problem-dependent, $\widetilde{\mathcal{O}}(\log{(KT)}),$ and problem-independent, $\widetilde{\mathcal{O}}(\sqrt{KT})$, regret bounds of near-optimal stochastic algorithms as UCB1 of Auer et al. (2002a). This result substantially improves the prior result of Levine et al. (2017) which needed knowledge of the horizon and decaying parameters to achieve problem-independent bound of only $\widetilde{\mathcal{O}}(K^{1/3}T^{2/3})$. Finally, we report simulations confirming the theoretical improvements of FEWA.

An Adaptive Strategy for Active Learning with Smooth Decision Boundary

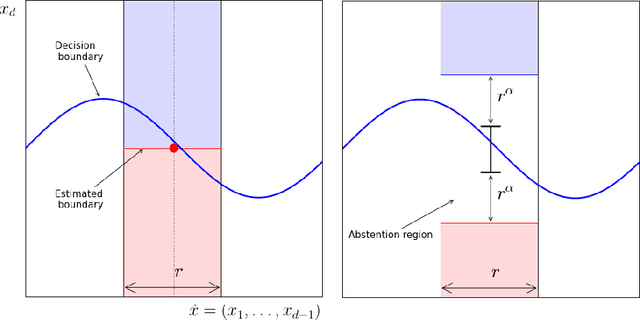
We present the first adaptive strategy for active learning in the setting of classification with smooth decision boundary. The problem of adaptivity (to unknown distributional parameters) has remained opened since the seminal work of Castro and Nowak (2007), which first established (active learning) rates for this setting. While some recent advances on this problem establish adaptive rates in the case of univariate data, adaptivity in the more practical setting of multivariate data has so far remained elusive. Combining insights from various recent works, we show that, for the multivariate case, a careful reduction to univariate-adaptive strategies yield near-optimal rates without prior knowledge of distributional parameters.

Adaptivity to Noise Parameters in Nonparametric Active Learning

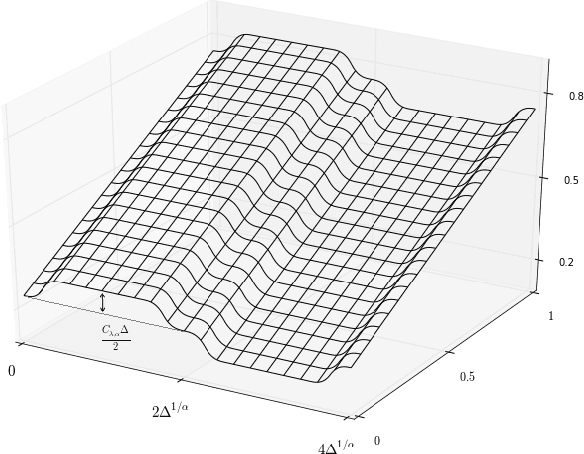
This work addresses various open questions in the theory of active learning for nonparametric classification. Our contributions are both statistical and algorithmic: -We establish new minimax-rates for active learning under common \textit{noise conditions}. These rates display interesting transitions -- due to the interaction between noise \textit{smoothness and margin} -- not present in the passive setting. Some such transitions were previously conjectured, but remained unconfirmed. -We present a generic algorithmic strategy for adaptivity to unknown noise smoothness and margin; our strategy achieves optimal rates in many general situations; furthermore, unlike in previous work, we avoid the need for \textit{adaptive confidence sets}, resulting in strictly milder distributional requirements.

Tight Bounds for the Fixed Budget Best Arm Identification Bandit Problem

We consider the problem of \textit{best arm identification} with a \textit{fixed budget $T$}, in the $K$-armed stochastic bandit setting, with arms distribution defined on $[0,1]$. We prove that any bandit strategy, for at least one bandit problem characterized by a complexity $H$, will misidentify the best arm with probability lower bounded by $$\exp\Big(-\frac{T}{\log(K)H}\Big),$$ where $H$ is the sum for all sub-optimal arms of the inverse of the squared gaps. Our result disproves formally the general belief - coming from results in the fixed confidence setting - that there must exist an algorithm for this problem whose probability of error is upper bounded by $\exp(-T/H)$. This also proves that some existing strategies based on the Successive Rejection of the arms are optimal - closing therefore the current gap between upper and lower bounds for the fixed budget best arm identification problem.

An optimal algorithm for the Thresholding Bandit Problem

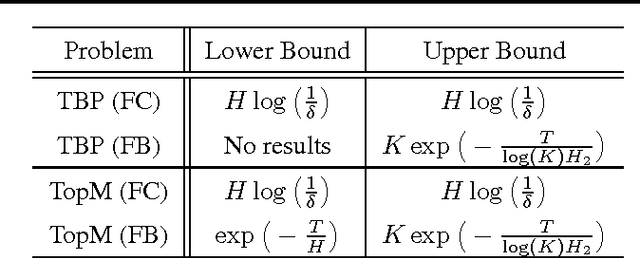
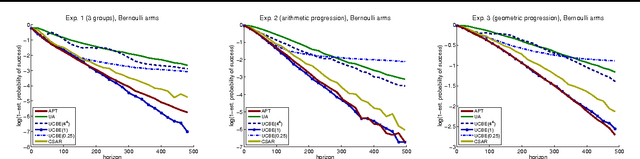
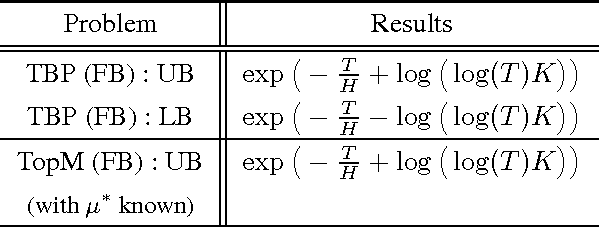
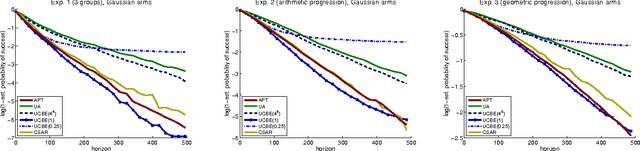
We study a specific \textit{combinatorial pure exploration stochastic bandit problem} where the learner aims at finding the set of arms whose means are above a given threshold, up to a given precision, and \textit{for a fixed time horizon}. We propose a parameter-free algorithm based on an original heuristic, and prove that it is optimal for this problem by deriving matching upper and lower bounds. To the best of our knowledge, this is the first non-trivial pure exploration setting with \textit{fixed budget} for which optimal strategies are constructed.