Improved Analysis of UCRL2 with Empirical Bernstein Inequality

We consider the problem of exploration-exploitation in communicating Markov Decision Processes. We provide an analysis of UCRL2 with Empirical Bernstein inequalities (UCRL2B). For any MDP with $S$ states, $A$ actions, $\Gamma \leq S$ next states and diameter $D$, the regret of UCRL2B is bounded as $\widetilde{O}(\sqrt{D\Gamma S A T})$.

Concentration Inequalities for Multinoulli Random Variables

We investigate concentration inequalities for Dirichlet and Multinomial random variables.

Exploration Bonus for Regret Minimization in Undiscounted Discrete and Continuous Markov Decision Processes

We introduce and analyse two algorithms for exploration-exploitation in discrete and continuous Markov Decision Processes (MDPs) based on exploration bonuses. SCAL$^+$ is a variant of SCAL (Fruit et al., 2018) that performs efficient exploration-exploitation in any unknown weakly-communicating MDP for which an upper bound C on the span of the optimal bias function is known. For an MDP with $S$ states, $A$ actions and $\Gamma \leq S$ possible next states, we prove that SCAL$^+$ achieves the same theoretical guarantees as SCAL (i.e., a high probability regret bound of $\widetilde{O}(C\sqrt{\Gamma SAT})$), with a much smaller computational complexity. Similarly, C-SCAL$^+$ exploits an exploration bonus to achieve sublinear regret in any undiscounted MDP with continuous state space. We show that C-SCAL$^+$ achieves the same regret bound as UCCRL (Ortner and Ryabko, 2012) while being the first implementable algorithm with regret guarantees in this setting. While optimistic algorithms such as UCRL, SCAL or UCCRL maintain a high-confidence set of plausible MDPs around the true unknown MDP, SCAL$^+$ and C-SCAL$^+$ leverage on an exploration bonus to directly plan on the empirically estimated MDP, thus being more computationally efficient.

Efficient Bias-Span-Constrained Exploration-Exploitation in Reinforcement Learning

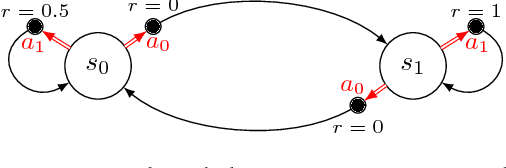
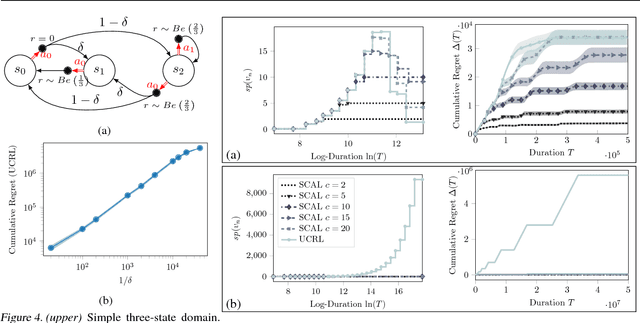
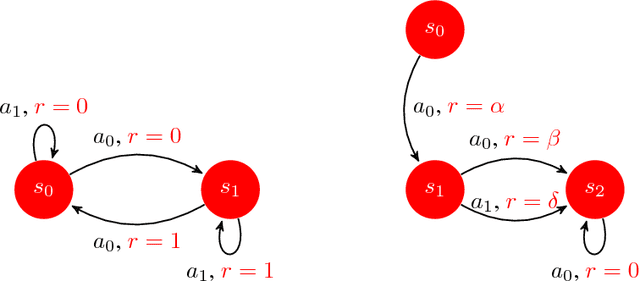
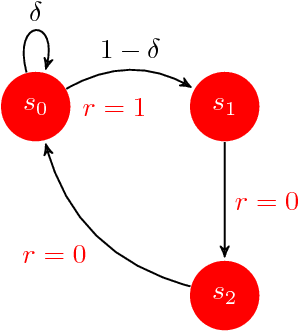
We introduce SCAL, an algorithm designed to perform efficient exploration-exploitation in any unknown weakly-communicating Markov decision process (MDP) for which an upper bound $c$ on the span of the optimal bias function is known. For an MDP with $S$ states, $A$ actions and $\Gamma \leq S$ possible next states, we prove a regret bound of $\widetilde{O}(c\sqrt{\Gamma SAT})$, which significantly improves over existing algorithms (e.g., UCRL and PSRL), whose regret scales linearly with the MDP diameter $D$. In fact, the optimal bias span is finite and often much smaller than $D$ (e.g., $D=\infty$ in non-communicating MDPs). A similar result was originally derived by Bartlett and Tewari (2009) for REGAL.C, for which no tractable algorithm is available. In this paper, we relax the optimization problem at the core of REGAL.C, we carefully analyze its properties, and we provide the first computationally efficient algorithm to solve it. Finally, we report numerical simulations supporting our theoretical findings and showing how SCAL significantly outperforms UCRL in MDPs with large diameter and small span.

Near Optimal Exploration-Exploitation in Non-Communicating Markov Decision Processes

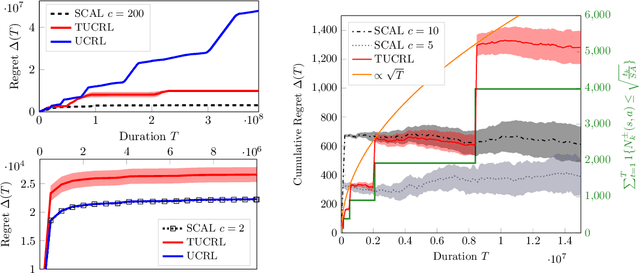
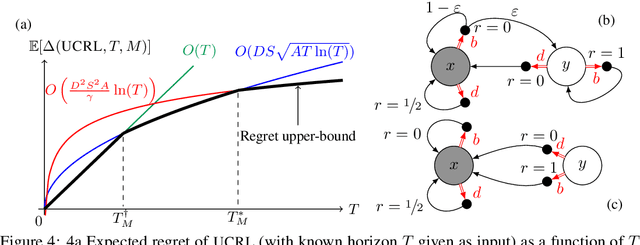
While designing the state space of an MDP, it is common to include states that are transient or not reachable by any policy (e.g., in mountain car, the product space of speed and position contains configurations that are not physically reachable). This leads to defining weakly-communicating or multi-chain MDPs. In this paper, we introduce \tucrl, the first algorithm able to perform efficient exploration-exploitation in any finite Markov Decision Process (MDP) without requiring any form of prior knowledge. In particular, for any MDP with $S^{\texttt{C}}$ communicating states, $A$ actions and $\Gamma^{\texttt{C}} \leq S^{\texttt{C}}$ possible communicating next states, we derive a $\widetilde{O}(D^{\texttt{C}} \sqrt{\Gamma^{\texttt{C}} S^{\texttt{C}} AT})$ regret bound, where $D^{\texttt{C}}$ is the diameter (i.e., the longest shortest path) of the communicating part of the MDP. This is in contrast with optimistic algorithms (e.g., UCRL, Optimistic PSRL) that suffer linear regret in weakly-communicating MDPs, as well as posterior sampling or regularised algorithms (e.g., REGAL), which require prior knowledge on the bias span of the optimal policy to bias the exploration to achieve sub-linear regret. We also prove that in weakly-communicating MDPs, no algorithm can ever achieve a logarithmic growth of the regret without first suffering a linear regret for a number of steps that is exponential in the parameters of the MDP. Finally, we report numerical simulations supporting our theoretical findings and showing how TUCRL overcomes the limitations of the state-of-the-art.

Exploration--Exploitation in MDPs with Options

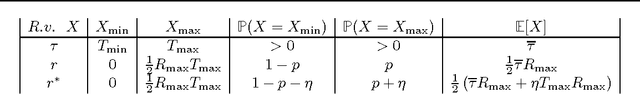
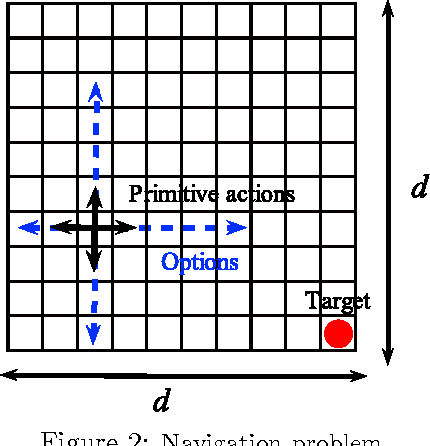
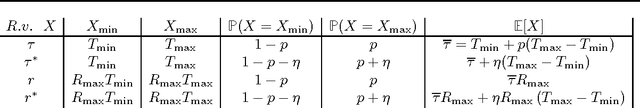
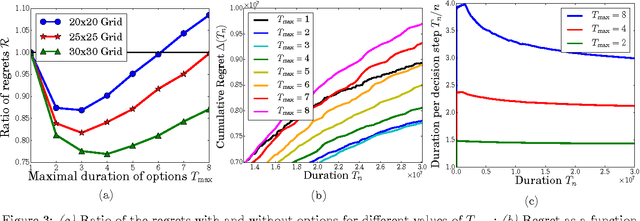
While a large body of empirical results show that temporally-extended actions and options may significantly affect the learning performance of an agent, the theoretical understanding of how and when options can be beneficial in online reinforcement learning is relatively limited. In this paper, we derive an upper and lower bound on the regret of a variant of UCRL using options. While we first analyze the algorithm in the general case of semi-Markov decision processes (SMDPs), we show how these results can be translated to the specific case of MDPs with options and we illustrate simple scenarios in which the regret of learning with options can be \textit{provably} much smaller than the regret suffered when learning with primitive actions.