Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

Structured Inverse-Free Natural Gradient: Memory-Efficient & Numerically-Stable KFAC for Large Neural Nets

Second-order methods for deep learning -- such as KFAC -- can be useful for neural net training. However, they are often memory-inefficient and numerically unstable for low-precision training since their preconditioning Kronecker factors are dense, and require high-precision matrix inversion or decomposition. Consequently, such methods are not widely used for training large neural networks such as transformer-based models. We address these two issues by (i) formulating an inverse-free update of KFAC and (ii) imposing structures in each of the Kronecker factors, resulting in a method we term structured inverse-free natural gradient descent (SINGD). On large modern neural networks, we show that, in contrast to KFAC, SINGD is memory efficient and numerically robust, and often outperforms AdamW even in half precision. Hence, our work closes a gap between first-order and second-order methods in modern low precision training for large neural nets.

Preventing Arbitrarily High Confidence on Far-Away Data in Point-Estimated Discriminative Neural Networks

Discriminatively trained, deterministic neural networks are the de facto choice for classification problems. However, even though they achieve state-of-the-art results on in-domain test sets, they tend to be overconfident on out-of-distribution (OOD) data. For instance, ReLU networks -- a popular class of neural network architectures -- have been shown to almost always yield high confidence predictions when the test data are far away from the training set, even when they are trained with OOD data. We overcome this problem by adding a term to the output of the neural network that corresponds to the logit of an extra class, that we design to dominate the logits of the original classes as we move away from the training data.This technique provably prevents arbitrarily high confidence on far-away test data while maintaining a simple discriminative point-estimate training. Evaluation on various benchmarks demonstrates strong performance against competitive baselines on both far-away and realistic OOD data.

On the Disconnect Between Theory and Practice of Overparametrized Neural Networks

The infinite-width limit of neural networks (NNs) has garnered significant attention as a theoretical framework for analyzing the behavior of large-scale, overparametrized networks. By approaching infinite width, NNs effectively converge to a linear model with features characterized by the neural tangent kernel (NTK). This establishes a connection between NNs and kernel methods, the latter of which are well understood. Based on this link, theoretical benefits and algorithmic improvements have been hypothesized and empirically demonstrated in synthetic architectures. These advantages include faster optimization, reliable uncertainty quantification and improved continual learning. However, current results quantifying the rate of convergence to the kernel regime suggest that exploiting these benefits requires architectures that are orders of magnitude wider than they are deep. This assumption raises concerns that practically relevant architectures do not exhibit behavior as predicted via the NTK. In this work, we empirically investigate whether the limiting regime either describes the behavior of large-width architectures used in practice or is informative for algorithmic improvements. Our empirical results demonstrate that this is not the case in optimization, uncertainty quantification or continual learning. This observed disconnect between theory and practice calls into question the practical relevance of the infinite-width limit.

Promises and Pitfalls of the Linearized Laplace in Bayesian Optimization

The linearized-Laplace approximation (LLA) has been shown to be effective and efficient in constructing Bayesian neural networks. It is theoretically compelling since it can be seen as a Gaussian process posterior with the mean function given by the neural network's maximum-a-posteriori predictive function and the covariance function induced by the empirical neural tangent kernel. However, while its efficacy has been studied in large-scale tasks like image classification, it has not been studied in sequential decision-making problems like Bayesian optimization where Gaussian processes -- with simple mean functions and kernels such as the radial basis function -- are the de-facto surrogate models. In this work, we study the usefulness of the LLA in Bayesian optimization and highlight its strong performance and flexibility. However, we also present some pitfalls that might arise and a potential problem with the LLA when the search space is unbounded.

The Geometry of Neural Nets' Parameter Spaces Under Reparametrization

Model reparametrization -- transforming the parameter space via a bijective differentiable map -- is a popular way to improve the training of neural networks. But reparametrizations have also been problematic since they induce inconsistencies in, e.g., Hessian-based flatness measures, optimization trajectories, and modes of probability density functions. This complicates downstream analyses, e.g. one cannot make a definitive statement about the connection between flatness and generalization. In this work, we study the invariance quantities of neural nets under reparametrization from the perspective of Riemannian geometry. We show that this notion of invariance is an inherent property of any neural net, as long as one acknowledges the assumptions about the metric that is always present, albeit often implicitly, and uses the correct transformation rules under reparametrization. We present discussions on measuring the flatness of minima, in optimization, and in probability-density maximization, along with applications in studying the biases of optimizers and in Bayesian inference.

Posterior Refinement Improves Sample Efficiency in Bayesian Neural Networks

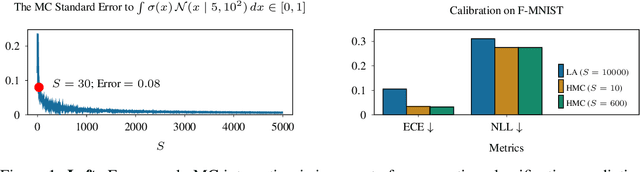
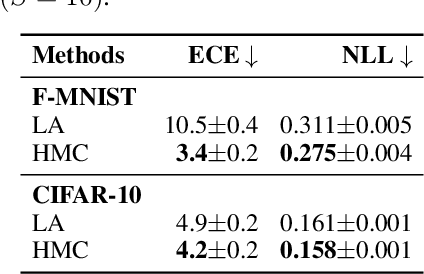
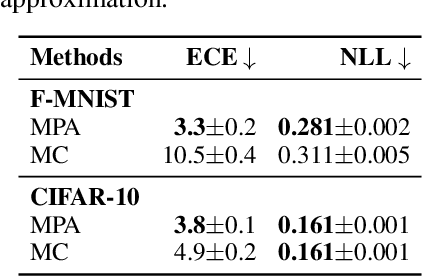
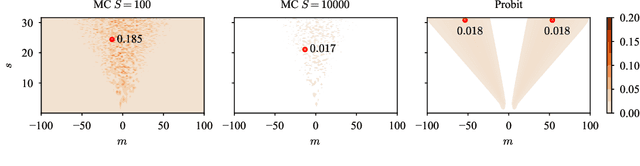
Monte Carlo (MC) integration is the de facto method for approximating the predictive distribution of Bayesian neural networks (BNNs). But, even with many MC samples, Gaussian-based BNNs could still yield bad predictive performance due to the posterior approximation's error. Meanwhile, alternatives to MC integration tend to be more expensive or biased. In this work, we experimentally show that the key to good MC-approximated predictive distributions is the quality of the approximate posterior itself. However, previous methods for obtaining accurate posterior approximations are expensive and non-trivial to implement. We, therefore, propose to refine Gaussian approximate posteriors with normalizing flows. When applied to last-layer BNNs, it yields a simple \emph{post hoc} method for improving pre-existing parametric approximations. We show that the resulting posterior approximation is competitive with even the gold-standard full-batch Hamiltonian Monte Carlo.

Discovering Inductive Bias with Gibbs Priors: A Diagnostic Tool for Approximate Bayesian Inference

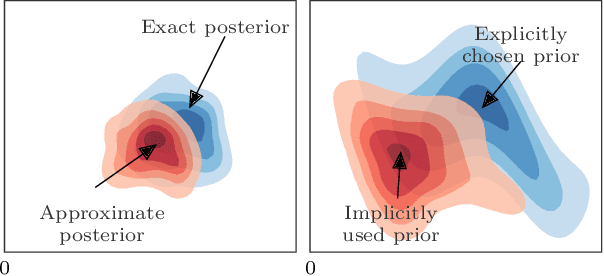
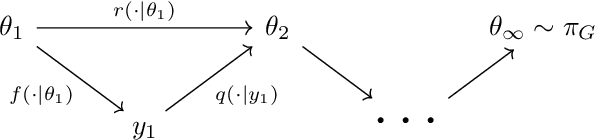
Full Bayesian posteriors are rarely analytically tractable, which is why real-world Bayesian inference heavily relies on approximate techniques. Approximations generally differ from the true posterior and require diagnostic tools to assess whether the inference can still be trusted. We investigate a new approach to diagnosing approximate inference: the approximation mismatch is attributed to a change in the inductive bias by treating the approximations as exact and reverse-engineering the corresponding prior. We show that the problem is more complicated than it appears to be at first glance, because the solution generally depends on the observation. By reframing the problem in terms of incompatible conditional distributions we arrive at a natural solution: the Gibbs prior. The resulting diagnostic is based on pseudo-Gibbs sampling, which is widely applicable and easy to implement. We illustrate how the Gibbs prior can be used to discover the inductive bias in a controlled Gaussian setting and for a variety of Bayesian models and approximations.

Mixtures of Laplace Approximations for Improved Post-Hoc Uncertainty in Deep Learning

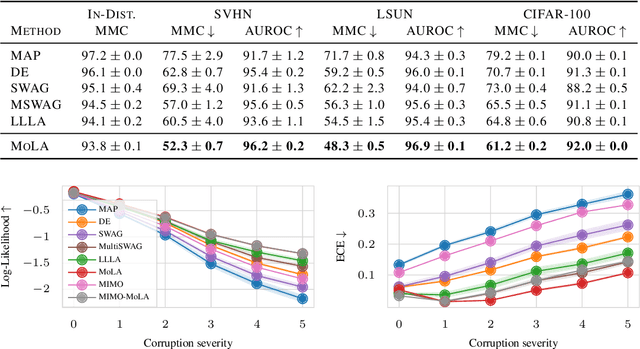
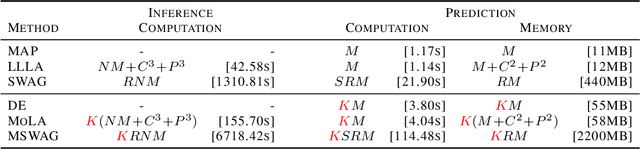
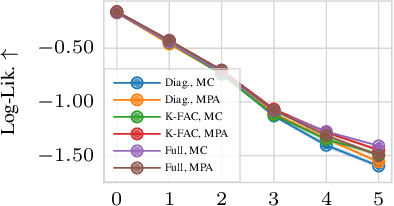
Deep neural networks are prone to overconfident predictions on outliers. Bayesian neural networks and deep ensembles have both been shown to mitigate this problem to some extent. In this work, we aim to combine the benefits of the two approaches by proposing to predict with a Gaussian mixture model posterior that consists of a weighted sum of Laplace approximations of independently trained deep neural networks. The method can be used post hoc with any set of pre-trained networks and only requires a small computational and memory overhead compared to regular ensembles. We theoretically validate that our approach mitigates overconfidence "far away" from the training data and empirically compare against state-of-the-art baselines on standard uncertainty quantification benchmarks.

Laplace Redux -- Effortless Bayesian Deep Learning

Bayesian formulations of deep learning have been shown to have compelling theoretical properties and offer practical functional benefits, such as improved predictive uncertainty quantification and model selection. The Laplace approximation (LA) is a classic, and arguably the simplest family of approximations for the intractable posteriors of deep neural networks. Yet, despite its simplicity, the LA is not as popular as alternatives like variational Bayes or deep ensembles. This may be due to assumptions that the LA is expensive due to the involved Hessian computation, that it is difficult to implement, or that it yields inferior results. In this work we show that these are misconceptions: we (i) review the range of variants of the LA including versions with minimal cost overhead; (ii) introduce "laplace", an easy-to-use software library for PyTorch offering user-friendly access to all major flavors of the LA; and (iii) demonstrate through extensive experiments that the LA is competitive with more popular alternatives in terms of performance, while excelling in terms of computational cost. We hope that this work will serve as a catalyst to a wider adoption of the LA in practical deep learning, including in domains where Bayesian approaches are not typically considered at the moment.