Computation-Aware Gaussian Processes: Model Selection And Linear-Time Inference

Model selection in Gaussian processes scales prohibitively with the size of the training dataset, both in time and memory. While many approximations exist, all incur inevitable approximation error. Recent work accounts for this error in the form of computational uncertainty, which enables -- at the cost of quadratic complexity -- an explicit tradeoff between computation and precision. Here we extend this development to model selection, which requires significant enhancements to the existing approach, including linear-time scaling in the size of the dataset. We propose a novel training loss for hyperparameter optimization and demonstrate empirically that the resulting method can outperform SGPR, CGGP and SVGP, state-of-the-art methods for GP model selection, on medium to large-scale datasets. Our experiments show that model selection for computation-aware GPs trained on 1.8 million data points can be done within a few hours on a single GPU. As a result of this work, Gaussian processes can be trained on large-scale datasets without significantly compromising their ability to quantify uncertainty -- a fundamental prerequisite for optimal decision-making.

Computation-Aware Kalman Filtering and Smoothing

Kalman filtering and smoothing are the foundational mechanisms for efficient inference in Gauss-Markov models. However, their time and memory complexities scale prohibitively with the size of the state space. This is particularly problematic in spatiotemporal regression problems, where the state dimension scales with the number of spatial observations. Existing approximate frameworks leverage low-rank approximations of the covariance matrix. Since they do not model the error introduced by the computational approximation, their predictive uncertainty estimates can be overly optimistic. In this work, we propose a probabilistic numerical method for inference in high-dimensional Gauss-Markov models which mitigates these scaling issues. Our matrix-free iterative algorithm leverages GPU acceleration and crucially enables a tunable trade-off between computational cost and predictive uncertainty. Finally, we demonstrate the scalability of our method on a large-scale climate dataset.

Accelerating Generalized Linear Models by Trading off Computation for Uncertainty

Bayesian Generalized Linear Models (GLMs) define a flexible probabilistic framework to model categorical, ordinal and continuous data, and are widely used in practice. However, exact inference in GLMs is prohibitively expensive for large datasets, thus requiring approximations in practice. The resulting approximation error adversely impacts the reliability of the model and is not accounted for in the uncertainty of the prediction. In this work, we introduce a family of iterative methods that explicitly model this error. They are uniquely suited to parallel modern computing hardware, efficiently recycle computations, and compress information to reduce both the time and memory requirements for GLMs. As we demonstrate on a realistically large classification problem, our method significantly accelerates training by explicitly trading off reduced computation for increased uncertainty.

Large-Scale Gaussian Processes via Alternating Projection

Gaussian process (GP) hyperparameter optimization requires repeatedly solving linear systems with $n \times n$ kernel matrices. To address the prohibitive $\mathcal{O}(n^3)$ time complexity, recent work has employed fast iterative numerical methods, like conjugate gradients (CG). However, as datasets increase in magnitude, the corresponding kernel matrices become increasingly ill-conditioned and still require $\mathcal{O}(n^2)$ space without partitioning. Thus, while CG increases the size of datasets GPs can be trained on, modern datasets reach scales beyond its applicability. In this work, we propose an iterative method which only accesses subblocks of the kernel matrix, effectively enabling \emph{mini-batching}. Our algorithm, based on alternating projection, has $\mathcal{O}(n)$ per-iteration time and space complexity, solving many of the practical challenges of scaling GPs to very large datasets. Theoretically, we prove our method enjoys linear convergence and empirically we demonstrate its robustness to ill-conditioning. On large-scale benchmark datasets up to four million datapoints our approach accelerates training by a factor of 2$\times$ to 27$\times$ compared to CG.

On the Disconnect Between Theory and Practice of Overparametrized Neural Networks

The infinite-width limit of neural networks (NNs) has garnered significant attention as a theoretical framework for analyzing the behavior of large-scale, overparametrized networks. By approaching infinite width, NNs effectively converge to a linear model with features characterized by the neural tangent kernel (NTK). This establishes a connection between NNs and kernel methods, the latter of which are well understood. Based on this link, theoretical benefits and algorithmic improvements have been hypothesized and empirically demonstrated in synthetic architectures. These advantages include faster optimization, reliable uncertainty quantification and improved continual learning. However, current results quantifying the rate of convergence to the kernel regime suggest that exploiting these benefits requires architectures that are orders of magnitude wider than they are deep. This assumption raises concerns that practically relevant architectures do not exhibit behavior as predicted via the NTK. In this work, we empirically investigate whether the limiting regime either describes the behavior of large-width architectures used in practice or is informative for algorithmic improvements. Our empirical results demonstrate that this is not the case in optimization, uncertainty quantification or continual learning. This observed disconnect between theory and practice calls into question the practical relevance of the infinite-width limit.

Physics-Informed Gaussian Process Regression Generalizes Linear PDE Solvers

Linear partial differential equations (PDEs) are an important, widely applied class of mechanistic models, describing physical processes such as heat transfer, electromagnetism, and wave propagation. In practice, specialized numerical methods based on discretization are used to solve PDEs. They generally use an estimate of the unknown model parameters and, if available, physical measurements for initialization. Such solvers are often embedded into larger scientific models or analyses with a downstream application such that error quantification plays a key role. However, by entirely ignoring parameter and measurement uncertainty, classical PDE solvers may fail to produce consistent estimates of their inherent approximation error. In this work, we approach this problem in a principled fashion by interpreting solving linear PDEs as physics-informed Gaussian process (GP) regression. Our framework is based on a key generalization of a widely-applied theorem for conditioning GPs on a finite number of direct observations to observations made via an arbitrary bounded linear operator. Crucially, this probabilistic viewpoint allows to (1) quantify the inherent discretization error; (2) propagate uncertainty about the model parameters to the solution; and (3) condition on noisy measurements. Demonstrating the strength of this formulation, we prove that it strictly generalizes methods of weighted residuals, a central class of PDE solvers including collocation, finite volume, pseudospectral, and (generalized) Galerkin methods such as finite element and spectral methods. This class can thus be directly equipped with a structured error estimate and the capability to incorporate uncertain model parameters and observations. In summary, our results enable the seamless integration of mechanistic models as modular building blocks into probabilistic models.

Posterior and Computational Uncertainty in Gaussian Processes

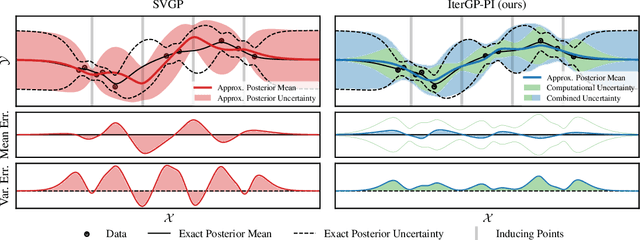
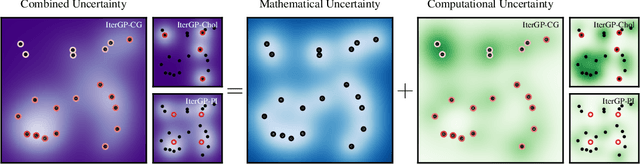
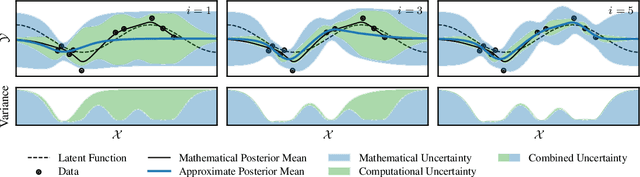
Gaussian processes scale prohibitively with the size of the dataset. In response, many approximation methods have been developed, which inevitably introduce approximation error. This additional source of uncertainty, due to limited computation, is entirely ignored when using the approximate posterior. Therefore in practice, GP models are often as much about the approximation method as they are about the data. Here, we develop a new class of methods that provides consistent estimation of the combined uncertainty arising from both the finite number of data observed and the finite amount of computation expended. The most common GP approximations map to an instance in this class, such as methods based on the Cholesky factorization, conjugate gradients, and inducing points. For any method in this class, we prove (i) convergence of its posterior mean in the associated RKHS, (ii) decomposability of its combined posterior covariance into mathematical and computational covariances, and (iii) that the combined variance is a tight worst-case bound for the squared error between the method's posterior mean and the latent function. Finally, we empirically demonstrate the consequences of ignoring computational uncertainty and show how implicitly modeling it improves generalization performance on benchmark datasets.

ProbNum: Probabilistic Numerics in Python

Probabilistic numerical methods (PNMs) solve numerical problems via probabilistic inference. They have been developed for linear algebra, optimization, integration and differential equation simulation. PNMs naturally incorporate prior information about a problem and quantify uncertainty due to finite computational resources as well as stochastic input. In this paper, we present ProbNum: a Python library providing state-of-the-art probabilistic numerical solvers. ProbNum enables custom composition of PNMs for specific problem classes via a modular design as well as wrappers for off-the-shelf use. Tutorials, documentation, developer guides and benchmarks are available online at www.probnum.org.

Reducing the Variance of Gaussian Process Hyperparameter Optimization with Preconditioning

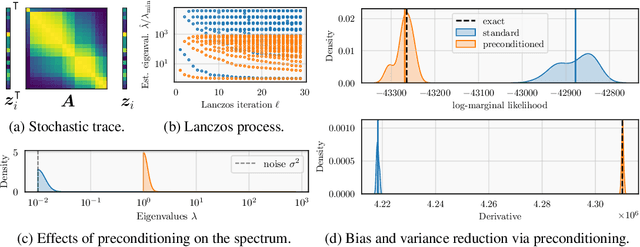
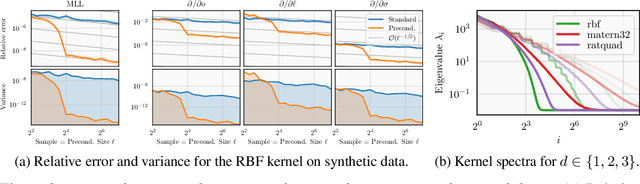
Gaussian processes remain popular as a flexible and expressive model class, but the computational cost of kernel hyperparameter optimization stands as a major limiting factor to their scaling and broader adoption. Recent work has made great strides combining stochastic estimation with iterative numerical techniques, essentially boiling down GP inference to the cost of (many) matrix-vector multiplies. Preconditioning -- a highly effective step for any iterative method involving matrix-vector multiplication -- can be used to accelerate convergence and thus reduce bias in hyperparameter optimization. Here, we prove that preconditioning has an additional benefit that has been previously unexplored. It not only reduces the bias of the $\log$-marginal likelihood estimator and its derivatives, but it also simultaneously can reduce variance at essentially negligible cost. We leverage this result to derive sample-efficient algorithms for GP hyperparameter optimization requiring as few as $\mathcal{O}(\log(\varepsilon^{-1}))$ instead of $\mathcal{O}(\varepsilon^{-2})$ samples to achieve error $\varepsilon$. Our theoretical results enable provably efficient and scalable optimization of kernel hyperparameters, which we validate empirically on a set of large-scale benchmark problems. There, variance reduction via preconditioning results in an order of magnitude speedup in hyperparameter optimization of exact GPs.

Probabilistic Linear Solvers for Machine Learning

Linear systems are the bedrock of virtually all numerical computation. Machine learning poses specific challenges for the solution of such systems due to their scale, characteristic structure, stochasticity and the central role of uncertainty in the field. Unifying earlier work we propose a class of probabilistic linear solvers which jointly infer the matrix, its inverse and the solution from matrix-vector product observations. This class emerges from a fundamental set of desiderata which constrains the space of possible algorithms and recovers the method of conjugate gradients under certain conditions. We demonstrate how to incorporate prior spectral information in order to calibrate uncertainty and experimentally showcase the potential of such solvers for machine learning.