GLEAM: Greedy Learning for Large-Scale Accelerated MRI Reconstruction

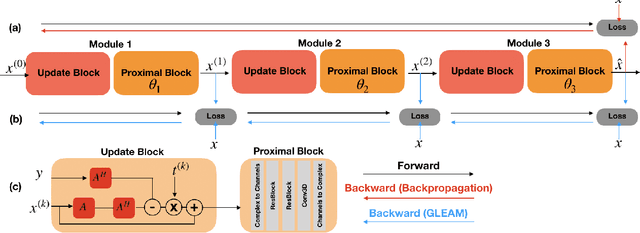
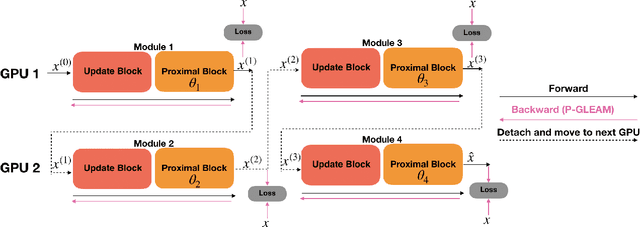
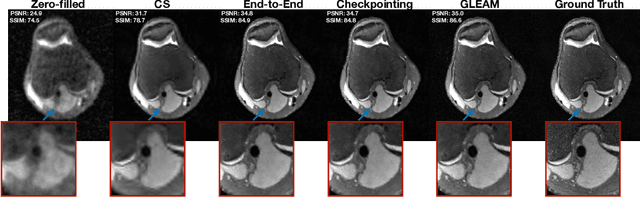
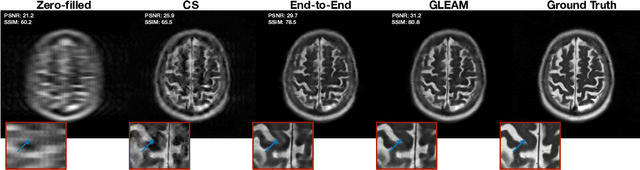
Unrolled neural networks have recently achieved state-of-the-art accelerated MRI reconstruction. These networks unroll iterative optimization algorithms by alternating between physics-based consistency and neural-network based regularization. However, they require several iterations of a large neural network to handle high-dimensional imaging tasks such as 3D MRI. This limits traditional training algorithms based on backpropagation due to prohibitively large memory and compute requirements for calculating gradients and storing intermediate activations. To address this challenge, we propose Greedy LEarning for Accelerated MRI (GLEAM) reconstruction, an efficient training strategy for high-dimensional imaging settings. GLEAM splits the end-to-end network into decoupled network modules. Each module is optimized in a greedy manner with decoupled gradient updates, reducing the memory footprint during training. We show that the decoupled gradient updates can be performed in parallel on multiple graphical processing units (GPUs) to further reduce training time. We present experiments with 2D and 3D datasets including multi-coil knee, brain, and dynamic cardiac cine MRI. We observe that: i) GLEAM generalizes as well as state-of-the-art memory-efficient baselines such as gradient checkpointing and invertible networks with the same memory footprint, but with 1.3x faster training; ii) for the same memory footprint, GLEAM yields 1.1dB PSNR gain in 2D and 1.8 dB in 3D over end-to-end baselines.

Unraveling Attention via Convex Duality: Analysis and Interpretations of Vision Transformers

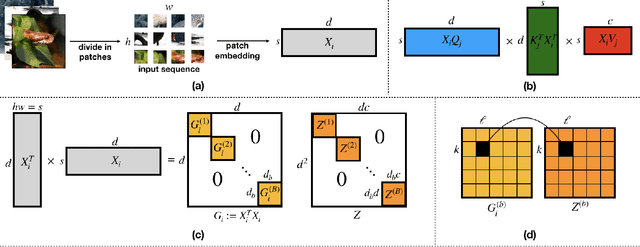
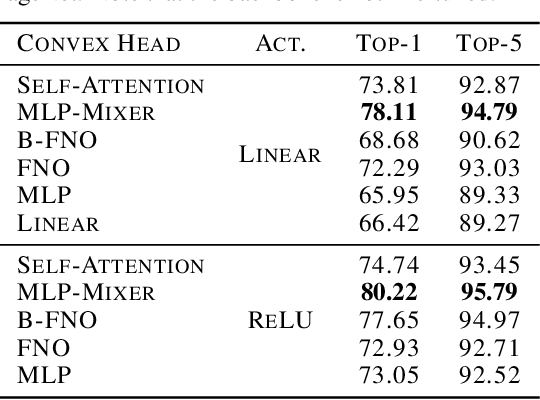
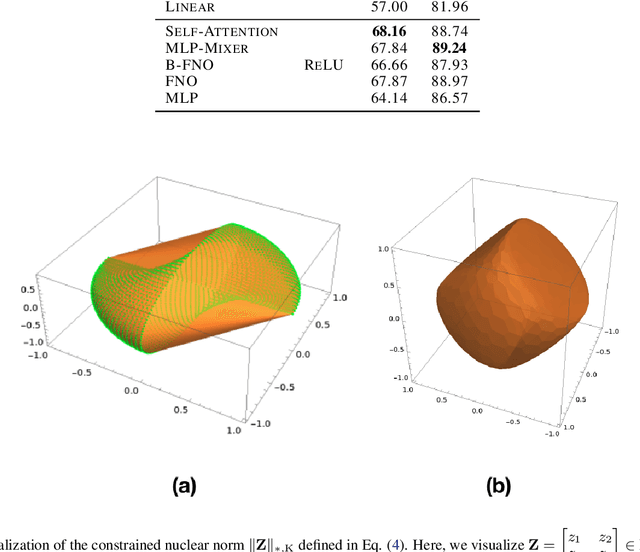
Vision transformers using self-attention or its proposed alternatives have demonstrated promising results in many image related tasks. However, the underpinning inductive bias of attention is not well understood. To address this issue, this paper analyzes attention through the lens of convex duality. For the non-linear dot-product self-attention, and alternative mechanisms such as MLP-mixer and Fourier Neural Operator (FNO), we derive equivalent finite-dimensional convex problems that are interpretable and solvable to global optimality. The convex programs lead to {\it block nuclear-norm regularization} that promotes low rank in the latent feature and token dimensions. In particular, we show how self-attention networks implicitly clusters the tokens, based on their latent similarity. We conduct experiments for transferring a pre-trained transformer backbone for CIFAR-100 classification by fine-tuning a variety of convex attention heads. The results indicate the merits of the bias induced by attention compared with the existing MLP or linear heads.

Scale-Equivariant Unrolled Neural Networks for Data-Efficient Accelerated MRI Reconstruction

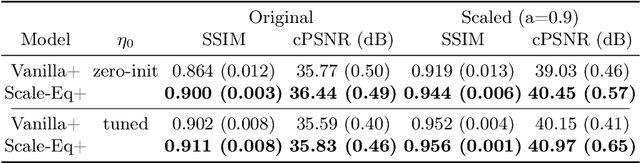
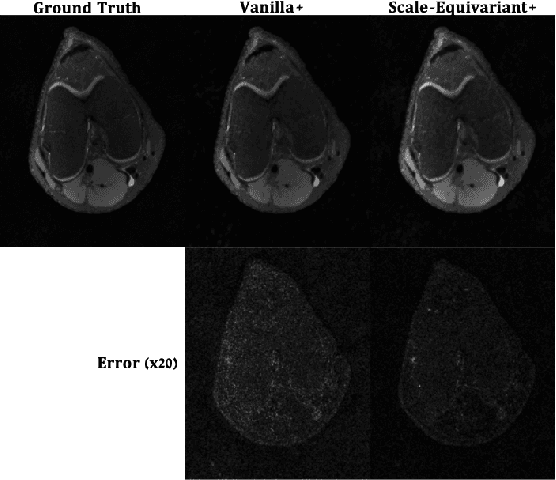
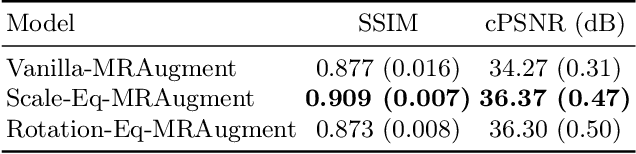
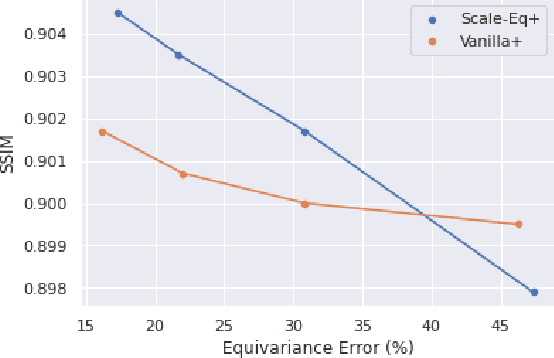
Unrolled neural networks have enabled state-of-the-art reconstruction performance and fast inference times for the accelerated magnetic resonance imaging (MRI) reconstruction task. However, these approaches depend on fully-sampled scans as ground truth data which is either costly or not possible to acquire in many clinical medical imaging applications; hence, reducing dependence on data is desirable. In this work, we propose modeling the proximal operators of unrolled neural networks with scale-equivariant convolutional neural networks in order to improve the data-efficiency and robustness to drifts in scale of the images that might stem from the variability of patient anatomies or change in field-of-view across different MRI scanners. Our approach demonstrates strong improvements over the state-of-the-art unrolled neural networks under the same memory constraints both with and without data augmentations on both in-distribution and out-of-distribution scaled images without significantly increasing the train or inference time.

Fast Convex Optimization for Two-Layer ReLU Networks: Equivalent Model Classes and Cone Decompositions

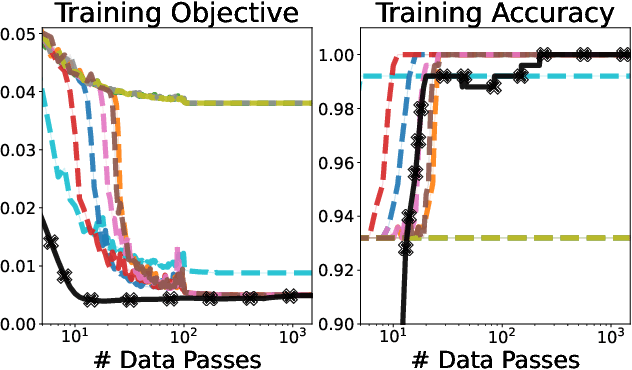
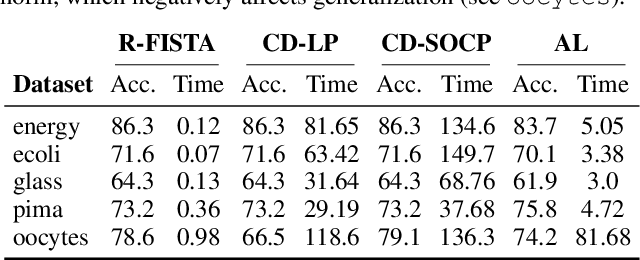
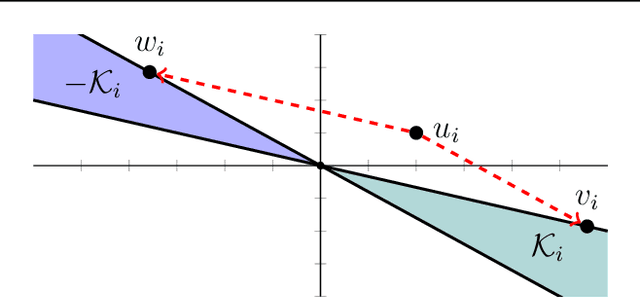
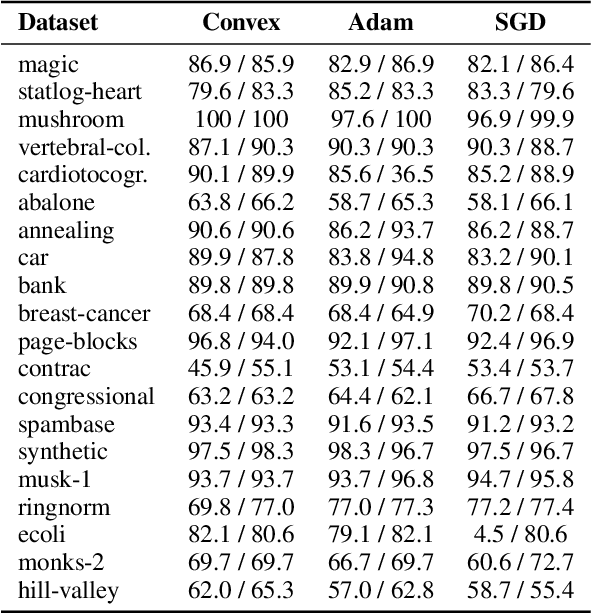
We develop fast algorithms and robust software for convex optimization of two-layer neural networks with ReLU activation functions. Our work leverages a convex reformulation of the standard weight-decay penalized training problem as a set of group-$\ell_1$-regularized data-local models, where locality is enforced by polyhedral cone constraints. In the special case of zero-regularization, we show that this problem is exactly equivalent to unconstrained optimization of a convex "gated ReLU" network. For problems with non-zero regularization, we show that convex gated ReLU models obtain data-dependent approximation bounds for the ReLU training problem. To optimize the convex reformulations, we develop an accelerated proximal gradient method and a practical augmented Lagrangian solver. We show that these approaches are faster than standard training heuristics for the non-convex problem, such as SGD, and outperform commercial interior-point solvers. Experimentally, we verify our theoretical results, explore the group-$\ell_1$ regularization path, and scale convex optimization for neural networks to image classification on MNIST and CIFAR-10.

Hidden Convexity of Wasserstein GANs: Interpretable Generative Models with Closed-Form Solutions

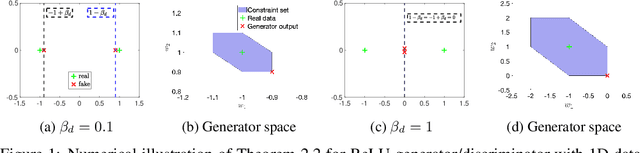
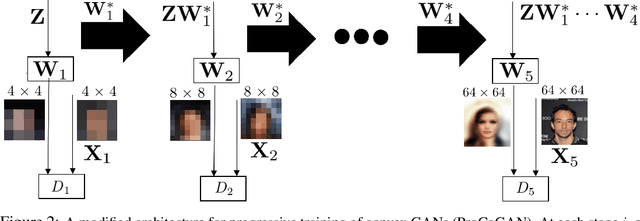
Generative Adversarial Networks (GANs) are commonly used for modeling complex distributions of data. Both the generators and discriminators of GANs are often modeled by neural networks, posing a non-transparent optimization problem which is non-convex and non-concave over the generator and discriminator, respectively. Such networks are often heuristically optimized with gradient descent-ascent (GDA), but it is unclear whether the optimization problem contains any saddle points, or whether heuristic methods can find them in practice. In this work, we analyze the training of Wasserstein GANs with two-layer neural network discriminators through the lens of convex duality, and for a variety of generators expose the conditions under which Wasserstein GANs can be solved exactly with convex optimization approaches, or can be represented as convex-concave games. Using this convex duality interpretation, we further demonstrate the impact of different activation functions of the discriminator. Our observations are verified with numerical results demonstrating the power of the convex interpretation, with applications in progressive training of convex architectures corresponding to linear generators and quadratic-activation discriminators for CelebA image generation. The code for our experiments is available at https://github.com/ardasahiner/ProCoGAN.

Demystifying Batch Normalization in ReLU Networks: Equivalent Convex Optimization Models and Implicit Regularization

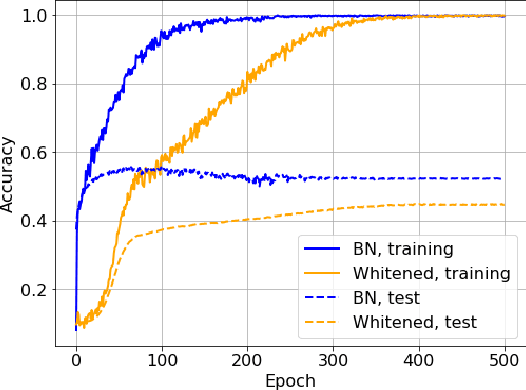
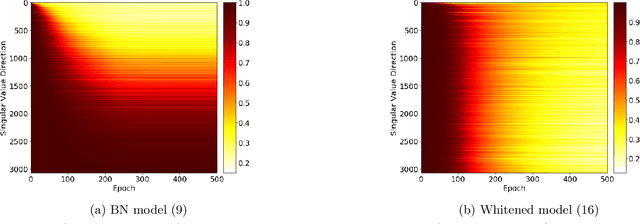
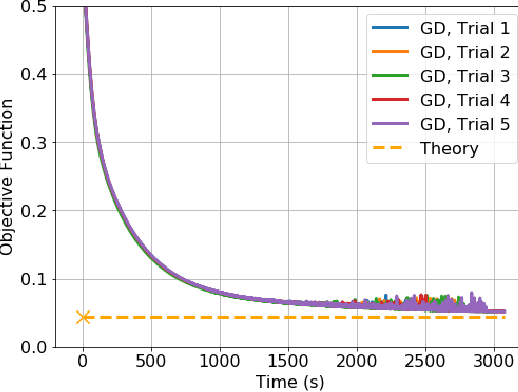
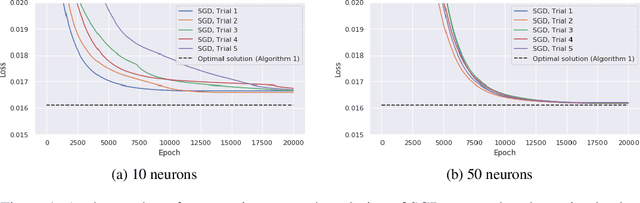
Batch Normalization (BN) is a commonly used technique to accelerate and stabilize training of deep neural networks. Despite its empirical success, a full theoretical understanding of BN is yet to be developed. In this work, we analyze BN through the lens of convex optimization. We introduce an analytic framework based on convex duality to obtain exact convex representations of weight-decay regularized ReLU networks with BN, which can be trained in polynomial-time. Our analyses also show that optimal layer weights can be obtained as simple closed-form formulas in the high-dimensional and/or overparameterized regimes. Furthermore, we find that Gradient Descent provides an algorithmic bias effect on the standard non-convex BN network, and we design an approach to explicitly encode this implicit regularization into the convex objective. Experiments with CIFAR image classification highlight the effectiveness of this explicit regularization for mimicking and substantially improving the performance of standard BN networks.

Vector-output ReLU Neural Network Problems are Copositive Programs: Convex Analysis of Two Layer Networks and Polynomial-time Algorithms

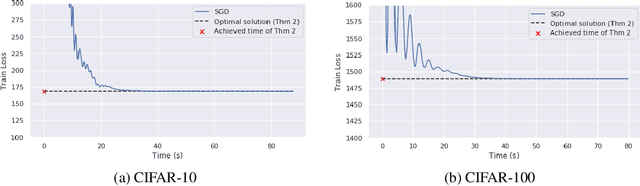
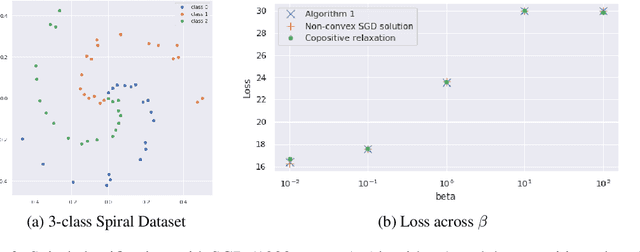
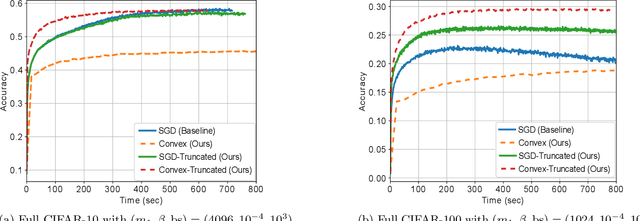
We describe the convex semi-infinite dual of the two-layer vector-output ReLU neural network training problem. This semi-infinite dual admits a finite dimensional representation, but its support is over a convex set which is difficult to characterize. In particular, we demonstrate that the non-convex neural network training problem is equivalent to a finite-dimensional convex copositive program. Our work is the first to identify this strong connection between the global optima of neural networks and those of copositive programs. We thus demonstrate how neural networks implicitly attempt to solve copositive programs via semi-nonnegative matrix factorization, and draw key insights from this formulation. We describe the first algorithms for provably finding the global minimum of the vector output neural network training problem, which are polynomial in the number of samples for a fixed data rank, yet exponential in the dimension. However, in the case of convolutional architectures, the computational complexity is exponential in only the filter size and polynomial in all other parameters. We describe the circumstances in which we can find the global optimum of this neural network training problem exactly with soft-thresholded SVD, and provide a copositive relaxation which is guaranteed to be exact for certain classes of problems, and which corresponds with the solution of Stochastic Gradient Descent in practice.

Convex Regularization Behind Neural Reconstruction

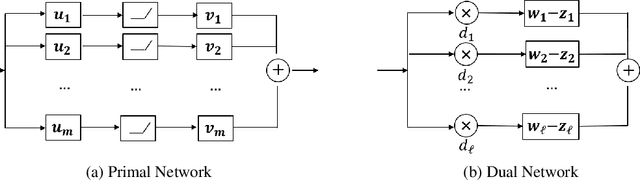
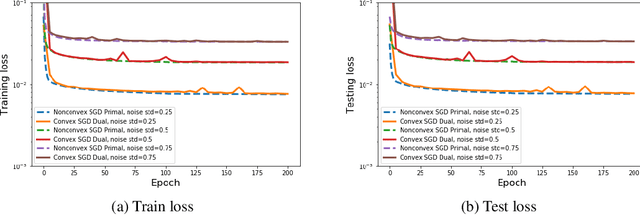
Neural networks have shown tremendous potential for reconstructing high-resolution images in inverse problems. The non-convex and opaque nature of neural networks, however, hinders their utility in sensitive applications such as medical imaging. To cope with this challenge, this paper advocates a convex duality framework that makes a two-layer fully-convolutional ReLU denoising network amenable to convex optimization. The convex dual network not only offers the optimum training with convex solvers, but also facilitates interpreting training and prediction. In particular, it implies training neural networks with weight decay regularization induces path sparsity while the prediction is piecewise linear filtering. A range of experiments with MNIST and fastMRI datasets confirm the efficacy of the dual network optimization problem.