Smoothing DiLoCo with Primal Averaging for Faster Training of LLMs

We propose Generalized Primal Averaging (GPA), an extension of Nesterov's method in its primal averaging formulation that addresses key limitations of recent averaging-based optimizers such as single-worker DiLoCo and Schedule-Free (SF) in the non-distributed setting. These two recent algorithmic approaches improve the performance of base optimizers, such as AdamW, through different iterate averaging strategies. Schedule-Free explicitly maintains a uniform average of past weights, while single-worker DiLoCo performs implicit averaging by periodically aggregating trajectories, called pseudo-gradients, to update the model parameters. However, single-worker DiLoCo's periodic averaging introduces a two-loop structure, increasing its memory requirements and number of hyperparameters. GPA overcomes these limitations by decoupling the interpolation constant in the primal averaging formulation of Nesterov. This decoupling enables GPA to smoothly average iterates at every step, generalizing and improving upon single-worker DiLoCo. Empirically, GPA consistently outperforms single-worker DiLoCo while removing the two-loop structure, simplifying hyperparameter tuning, and reducing its memory overhead to a single additional buffer. On the Llama-160M model, GPA provides a 24.22% speedup in terms of steps to reach the baseline (AdamW's) validation loss. Likewise, GPA achieves speedups of 12% and 27% on small and large batch setups, respectively, to attain AdamW's validation accuracy on the ImageNet ViT workload. Furthermore, we prove that for any base optimizer with regret bounded by $O(\sqrt{T})$, where $T$ is the number of iterations, GPA can match or exceed the convergence guarantee of the original optimizer, depending on the choice of interpolation constants.

PARQ: Piecewise-Affine Regularized Quantization

We develop a principled method for quantization-aware training (QAT) of large-scale machine learning models. Specifically, we show that convex, piecewise-affine regularization (PAR) can effectively induce the model parameters to cluster towards discrete values. We minimize PAR-regularized loss functions using an aggregate proximal stochastic gradient method (AProx) and prove that it has last-iterate convergence. Our approach provides an interpretation of the straight-through estimator (STE), a widely used heuristic for QAT, as the asymptotic form of PARQ. We conduct experiments to demonstrate that PARQ obtains competitive performance on convolution- and transformer-based vision tasks.

The Road Less Scheduled

Existing learning rate schedules that do not require specification of the optimization stopping step T are greatly out-performed by learning rate schedules that depend on T. We propose an approach that avoids the need for this stopping time by eschewing the use of schedules entirely, while exhibiting state-of-the-art performance compared to schedules across a wide family of problems ranging from convex problems to large-scale deep learning problems. Our Schedule-Free approach introduces no additional hyper-parameters over standard optimizers with momentum. Our method is a direct consequence of a new theory we develop that unifies scheduling and iterate averaging. An open source implementation of our method is available (https://github.com/facebookresearch/schedule_free).

Directional Smoothness and Gradient Methods: Convergence and Adaptivity

We develop new sub-optimality bounds for gradient descent (GD) that depend on the conditioning of the objective along the path of optimization, rather than on global, worst-case constants. Key to our proofs is directional smoothness, a measure of gradient variation that we use to develop upper-bounds on the objective. Minimizing these upper-bounds requires solving implicit equations to obtain a sequence of strongly adapted step-sizes; we show that these equations are straightforward to solve for convex quadratics and lead to new guarantees for two classical step-sizes. For general functions, we prove that the Polyak step-size and normalized GD obtain fast, path-dependent rates despite using no knowledge of the directional smoothness. Experiments on logistic regression show our convergence guarantees are tighter than the classical theory based on L-smoothness.

When, Why and How Much? Adaptive Learning Rate Scheduling by Refinement

Learning rate schedules used in practice bear little resemblance to those recommended by theory. We close much of this theory/practice gap, and as a consequence are able to derive new problem-adaptive learning rate schedules. Our key technical contribution is a refined analysis of learning rate schedules for a wide class of optimization algorithms (including SGD). In contrast to most prior works that study the convergence of the average iterate, we study the last iterate, which is what most people use in practice. When considering only worst-case analysis, our theory predicts that the best choice is the linear decay schedule: a popular choice in practice that sets the stepsize proportionally to $1 - t/T$, where $t$ is the current iteration and $T$ is the total number of steps. To go beyond this worst-case analysis, we use the observed gradient norms to derive schedules refined for any particular task. These refined schedules exhibit learning rate warm-up and rapid learning rate annealing near the end of training. Ours is the first systematic approach to automatically yield both of these properties. We perform the most comprehensive evaluation of learning rate schedules to date, evaluating across 10 diverse deep learning problems, a series of LLMs, and a suite of logistic regression problems. We validate that overall, the linear-decay schedule matches or outperforms all commonly used default schedules including cosine annealing, and that our schedule refinement method gives further improvements.

Prodigy: An Expeditiously Adaptive Parameter-Free Learner

We consider the problem of estimating the learning rate in adaptive methods, such as Adagrad and Adam. We describe two techniques, Prodigy and Resetting, to provably estimate the distance to the solution $D$, which is needed to set the learning rate optimally. Our techniques are modifications of the D-Adaptation method for learning-rate-free learning. Our methods improve upon the convergence rate of D-Adaptation by a factor of $O(\sqrt{\log(D/d_0)})$, where $d_0$ is the initial estimate of $D$. We test our methods on 12 common logistic-regression benchmark datasets, VGG11 and ResNet-50 training on CIFAR10, ViT training on Imagenet, LSTM training on IWSLT14, DLRM training on Criteo dataset, VarNet on Knee MRI dataset, as well as RoBERTa and GPT transformer training on BookWiki. Our experimental results show that our approaches consistently outperform D-Adaptation and reach test accuracy values close to that of hand-tuned Adam.

Mechanic: A Learning Rate Tuner

We introduce a technique for tuning the learning rate scale factor of any base optimization algorithm and schedule automatically, which we call \textsc{mechanic}. Our method provides a practical realization of recent theoretical reductions for accomplishing a similar goal in online convex optimization. We rigorously evaluate \textsc{mechanic} on a range of large scale deep learning tasks with varying batch sizes, schedules, and base optimization algorithms. These experiments demonstrate that depending on the problem, \textsc{mechanic} either comes very close to, matches or even improves upon manual tuning of learning rates.

MoMo: Momentum Models for Adaptive Learning Rates

We present new adaptive learning rates that can be used with any momentum method. To showcase our new learning rates we develop MoMo and MoMo-Adam, which are SGD with momentum (SGDM) and Adam together with our new adaptive learning rates. Our MoMo methods are motivated through model-based stochastic optimization, wherein we use momentum estimates of the batch losses and gradients sampled at each iteration to build a model of the loss function. Our model also makes use of any known lower bound of the loss function by using truncation. Indeed most losses are bounded below by zero. We then approximately minimize this model at each iteration to compute the next step. For losses with unknown lower bounds, we develop new on-the-fly estimates of the lower bound that we use in our model. Numerical experiments show that our MoMo methods improve over SGDM and Adam in terms of accuracy and robustness to hyperparameter tuning for training image classifiers on MNIST, CIFAR10, CIFAR100, Imagenet32, DLRM on the Criteo dataset, and a transformer model on the translation task IWSLT14.

Learning-Rate-Free Learning by D-Adaptation

The speed of gradient descent for convex Lipschitz functions is highly dependent on the choice of learning rate. Setting the learning rate to achieve the optimal convergence rate requires knowing the distance D from the initial point to the solution set. In this work, we describe a single-loop method, with no back-tracking or line searches, which does not require knowledge of $D$ yet asymptotically achieves the optimal rate of convergence for the complexity class of convex Lipschitz functions. Our approach is the first parameter-free method for this class without additional multiplicative log factors in the convergence rate. We present extensive experiments for SGD and Adam variants of our method, where the method automatically matches hand-tuned learning rates across more than a dozen diverse machine learning problems, including large-scale vision and language problems. Our method is practical, efficient and requires no additional function value or gradient evaluations each step. An open-source implementation is available (https://github.com/facebookresearch/dadaptation).

Grad-GradaGrad? A Non-Monotone Adaptive Stochastic Gradient Method

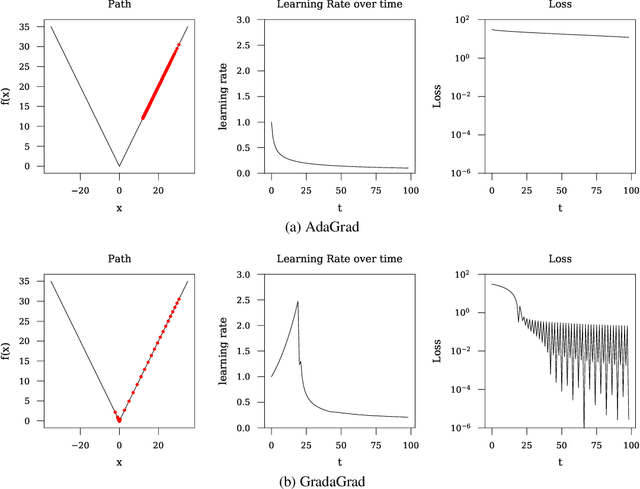
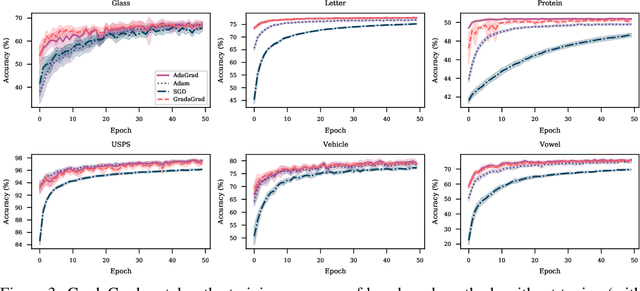
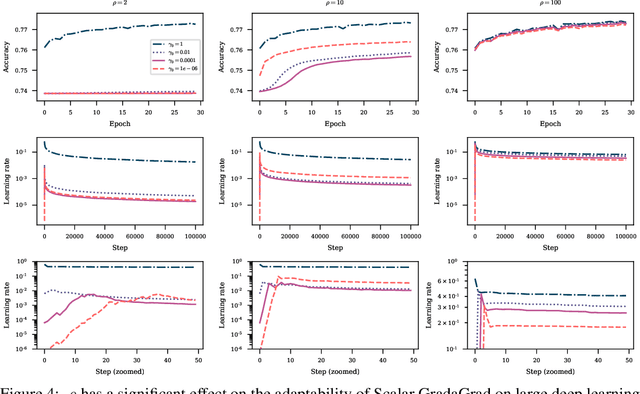
The classical AdaGrad method adapts the learning rate by dividing by the square root of a sum of squared gradients. Because this sum on the denominator is increasing, the method can only decrease step sizes over time, and requires a learning rate scaling hyper-parameter to be carefully tuned. To overcome this restriction, we introduce GradaGrad, a method in the same family that naturally grows or shrinks the learning rate based on a different accumulation in the denominator, one that can both increase and decrease. We show that it obeys a similar convergence rate as AdaGrad and demonstrate its non-monotone adaptation capability with experiments.