SAES-SVD: Self-Adaptive Suppression of Accumulated and Local Errors for SVD-based LLM Compression

The rapid growth in the parameter scale of large language models (LLMs) has created a high demand for efficient compression techniques. As a hardware-agnostic and highly compatible technique, low-rank compression has been widely adopted. However, existing methods typically compress each layer independently by minimizing per-layer reconstruction error, overlooking a critical limitation: the reconstruction error propagates and accumulates through the network, which leads to amplified global deviations from the full-precision baseline. To address this, we propose Self-Adaptive Error Suppression SVD (SAES-SVD), a LLMs compression framework that jointly optimizes intra-layer reconstruction and inter-layer error compensation. SAES-SVD is composed of two novel components: (1) Cumulative Error-Aware Layer Compression (CEALC), which formulates the compression objective as a combination of local reconstruction and weighted cumulative error compensation. Based on it, we derive a closed-form low-rank solution relied on second-order activation statistics, which explicitly aligns each layer's output with its full-precision counterpart to compensate for accumulated errors. (2) Adaptive Collaborative Error Suppression (ACES), which automatically adjusts the weighting coefficient to enhance the low-rank structure of the compression objective in CEALC. Specifically, the coefficient is optimized to maximize the ratio between the Frobenius norm of the compressed layer's output and that of the compression objective under a fixed rank, thus ensuring that the rank budget is utilized effectively. Extensive experiments across multiple LLM architectures and tasks show that, without fine-tuning or mixed-rank strategies, SAES-SVD consistently improves post-compression performance.

PCDVQ: Enhancing Vector Quantization for Large Language Models via Polar Coordinate Decoupling

Large Language Models (LLMs) face significant challenges in edge deployment due to their massive parameter scale. Vector Quantization (VQ), a clustering-based quantization method, serves as a prevalent solution to this issue for its extremely low-bit (even at 2-bit) and considerable accuracy. Since a vector is a quantity in mathematics and physics that has both direction and magnitude, existing VQ works typically quantize them in a coupled manner. However, we find that direction exhibits significantly greater sensitivity to quantization compared to the magnitude. For instance, when separately clustering the directions and magnitudes of weight vectors in LLaMA-2-7B, the accuracy drop of zero-shot tasks are 46.5\% and 2.3\%, respectively. This gap even increases with the reduction of clustering centers. Further, Euclidean distance, a common metric to access vector similarities in current VQ works, places greater emphasis on reducing the magnitude error. This property is contrary to the above finding, unavoidably leading to larger quantization errors. To these ends, this paper proposes Polar Coordinate Decoupled Vector Quantization (PCDVQ), an effective and efficient VQ framework consisting of two key modules: 1) Polar Coordinate Decoupling (PCD), which transforms vectors into their polar coordinate representations and perform independent quantization of the direction and magnitude parameters.2) Distribution Aligned Codebook Construction (DACC), which optimizes the direction and magnitude codebooks in accordance with the source distribution. Experimental results show that PCDVQ outperforms baseline methods at 2-bit level by at least 1.5\% zero-shot accuracy, establishing a novel paradigm for accurate and highly compressed LLMs.

RWKVQuant: Quantizing the RWKV Family with Proxy Guided Hybrid of Scalar and Vector Quantization

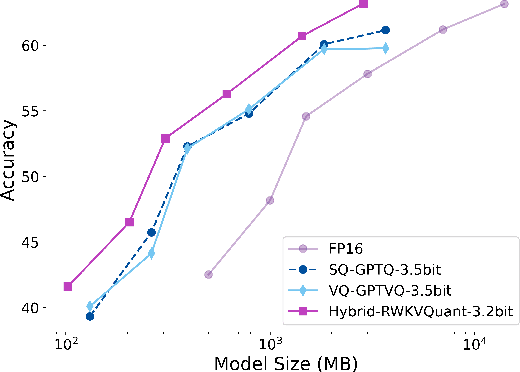
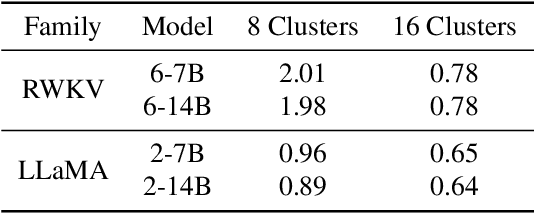
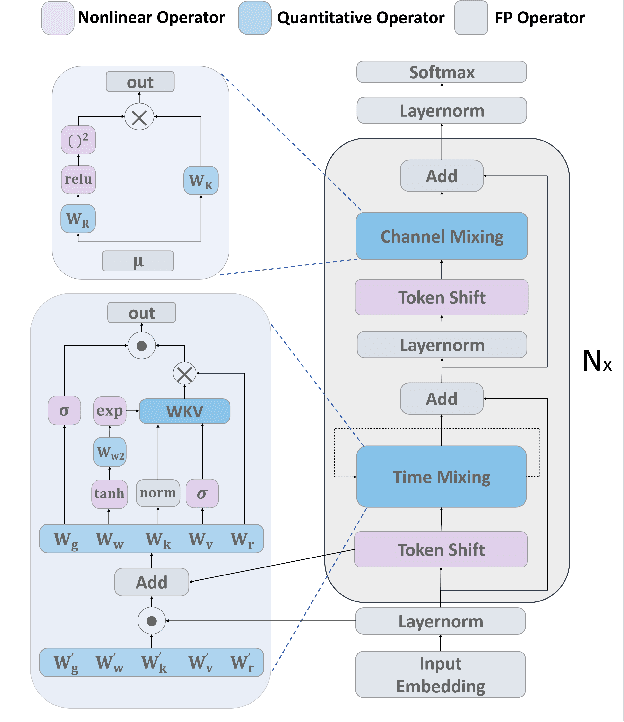
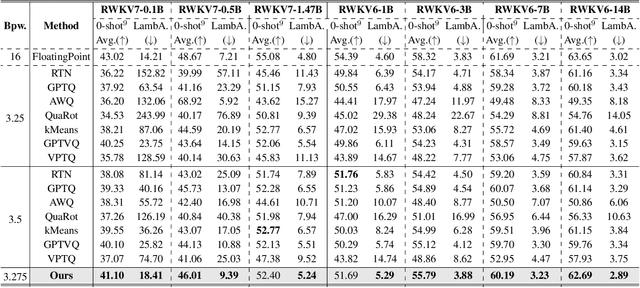
RWKV is a modern RNN architecture with comparable performance to Transformer, but still faces challenges when deployed to resource-constrained devices. Post Training Quantization (PTQ), which is a an essential technique to reduce model size and inference latency, has been widely used in Transformer models. However, it suffers significant degradation of performance when applied to RWKV. This paper investigates and identifies two key constraints inherent in the properties of RWKV: (1) Non-linear operators hinder the parameter-fusion of both smooth- and rotation-based quantization, introducing extra computation overhead. (2) The larger amount of uniformly distributed weights poses challenges for cluster-based quantization, leading to reduced accuracy. To this end, we propose RWKVQuant, a PTQ framework tailored for RWKV models, consisting of two novel techniques: (1) a coarse-to-fine proxy capable of adaptively selecting different quantization approaches by assessing the uniformity and identifying outliers in the weights, and (2) a codebook optimization algorithm that enhances the performance of cluster-based quantization methods for element-wise multiplication in RWKV. Experiments show that RWKVQuant can quantize RWKV-6-14B into about 3-bit with less than 1% accuracy loss and 2.14x speed up.

MoEQuant: Enhancing Quantization for Mixture-of-Experts Large Language Models via Expert-Balanced Sampling and Affinity Guidance

Mixture-of-Experts (MoE) large language models (LLMs), which leverage dynamic routing and sparse activation to enhance efficiency and scalability, have achieved higher performance while reducing computational costs. However, these models face significant memory overheads, limiting their practical deployment and broader adoption. Post-training quantization (PTQ), a widely used method for compressing LLMs, encounters severe accuracy degradation and diminished generalization performance when applied to MoE models. This paper investigates the impact of MoE's sparse and dynamic characteristics on quantization and identifies two primary challenges: (1) Inter-expert imbalance, referring to the uneven distribution of samples across experts, which leads to insufficient and biased calibration for less frequently utilized experts; (2) Intra-expert imbalance, arising from MoE's unique aggregation mechanism, which leads to varying degrees of correlation between different samples and their assigned experts. To address these challenges, we propose MoEQuant, a novel quantization framework tailored for MoE LLMs. MoE-Quant includes two novel techniques: 1) Expert-Balanced Self-Sampling (EBSS) is an efficient sampling method that efficiently constructs a calibration set with balanced expert distributions by leveraging the cumulative probabilities of tokens and expert balance metrics as guiding factors. 2) Affinity-Guided Quantization (AGQ), which incorporates affinities between experts and samples into the quantization process, thereby accurately assessing the impact of individual samples on different experts within the MoE layer. Experiments demonstrate that MoEQuant achieves substantial performance gains (more than 10 points accuracy gain in the HumanEval for DeepSeekMoE-16B under 4-bit quantization) and boosts efficiency.