Efficient Adaptive Regret Minimization

In online convex optimization the player aims to minimize her regret against a fixed comparator over the entire repeated game. Algorithms that minimize standard regret may converge to a fixed decision, which is undesireable in changing or dynamic environments. This motivates the stronger metric of adaptive regret, or the maximum regret over any continuous sub-interval in time. Existing adaptive regret algorithms suffer from a computational penalty - typically on the order of a multiplicative factor that grows logarithmically in the number of game iterations. In this paper we show how to reduce this computational penalty to be doubly logarithmic in the number of game iterations, and with minimal degradation to the optimal attainable adaptive regret bounds.

Adaptive Online Learning of Quantum States

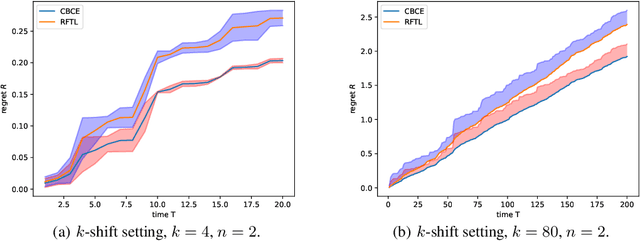
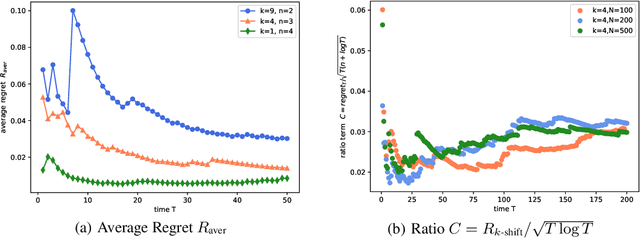
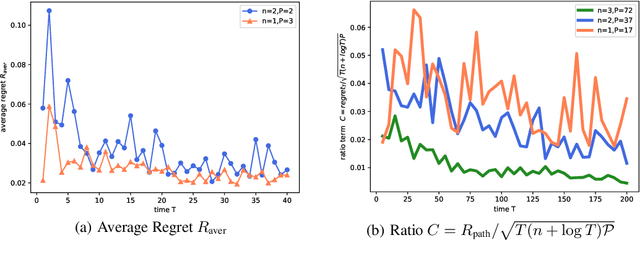
In the fundamental problem of shadow tomography, the goal is to efficiently learn an unknown $d$-dimensional quantum state using projective measurements. However, it is rarely the case that the underlying state remains stationary: changes may occur due to measurements, environmental noise, or an underlying Hamiltonian state evolution. In this paper we adopt tools from adaptive online learning to learn a changing state, giving adaptive and dynamic regret bounds for online shadow tomography that are polynomial in the number of qubits and sublinear in the number of measurements. Our analysis utilizes tools from complex matrix analysis to cope with complex numbers, which may be of independent interest in online learning. In addition, we provide numerical experiments that corroborate our theoretical results.

Non-convex online learning via algorithmic equivalence

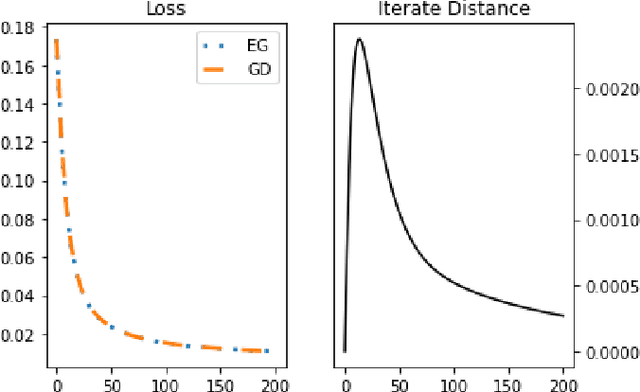
We study an algorithmic equivalence technique between nonconvex gradient descent and convex mirror descent. We start by looking at a harder problem of regret minimization in online non-convex optimization. We show that under certain geometric and smoothness conditions, online gradient descent applied to non-convex functions is an approximation of online mirror descent applied to convex functions under reparameterization. In continuous time, the gradient flow with this reparameterization was shown to be exactly equivalent to continuous-time mirror descent by Amid and Warmuth 2020, but theory for the analogous discrete time algorithms is left as an open problem. We prove an $O(T^{\frac{2}{3}})$ regret bound for non-convex online gradient descent in this setting, answering this open problem. Our analysis is based on a new and simple algorithmic equivalence method.

Adaptive Gradient Methods with Local Guarantees

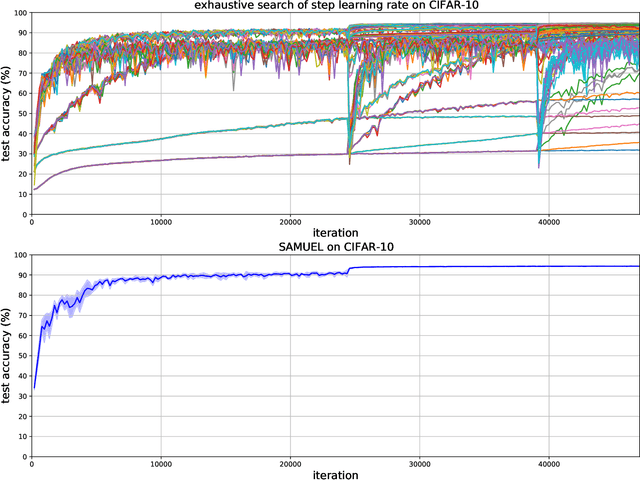
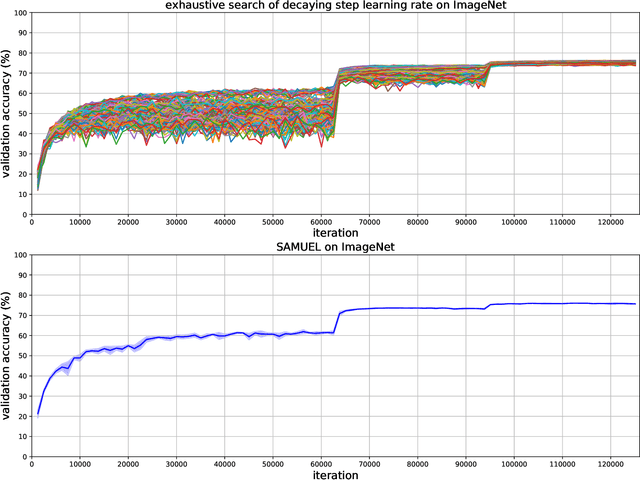
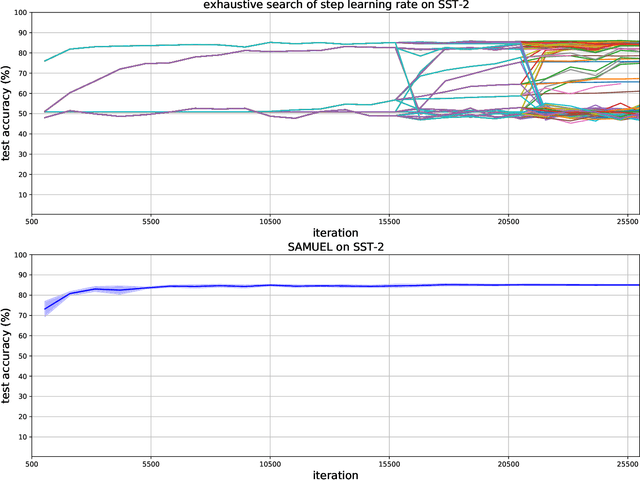
Adaptive gradient methods are the method of choice for optimization in machine learning and used to train the largest deep models. In this paper we study the problem of learning a local preconditioner, that can change as the data is changing along the optimization trajectory. We propose an adaptive gradient method that has provable adaptive regret guarantees vs. the best local preconditioner. To derive this guarantee, we prove a new adaptive regret bound in online learning that improves upon previous adaptive online learning methods. We demonstrate the robustness of our method in automatically choosing the optimal learning rate schedule for popular benchmarking tasks in vision and language domains. Without the need to manually tune a learning rate schedule, our method can, in a single run, achieve comparable and stable task accuracy as a fine-tuned optimizer.

The Convergence Rate of SGD's Final Iterate: Analysis on Dimension Dependence

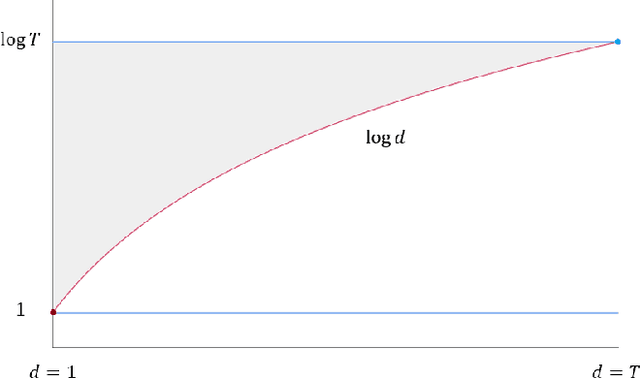
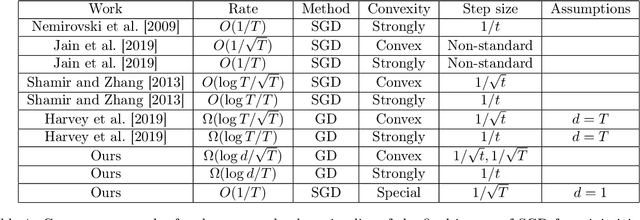
Stochastic Gradient Descent (SGD) is among the simplest and most popular methods in optimization. The convergence rate for SGD has been extensively studied and tight analyses have been established for the running average scheme, but the sub-optimality of the final iterate is still not well-understood. shamir2013stochastic gave the best known upper bound for the final iterate of SGD minimizing non-smooth convex functions, which is $O(\log T/\sqrt{T})$ for Lipschitz convex functions and $O(\log T/ T)$ with additional assumption on strongly convexity. The best known lower bounds, however, are worse than the upper bounds by a factor of $\log T$. harvey2019tight gave matching lower bounds but their construction requires dimension $d= T$. It was then asked by koren2020open how to characterize the final-iterate convergence of SGD in the constant dimension setting. In this paper, we answer this question in the more general setting for any $d\leq T$, proving $\Omega(\log d/\sqrt{T})$ and $\Omega(\log d/T)$ lower bounds for the sub-optimality of the final iterate of SGD in minimizing non-smooth Lipschitz convex and strongly convex functions respectively with standard step size schedules. Our results provide the first general dimension dependent lower bound on the convergence of SGD's final iterate, partially resolving a COLT open question raised by koren2020open. We also present further evidence to show the correct rate in one dimension should be $\Theta(1/\sqrt{T})$, such as a proof of a tight $O(1/\sqrt{T})$ upper bound for one-dimensional special cases in settings more general than koren2020open.

Curse of Dimensionality in Unconstrained Private Convex ERM

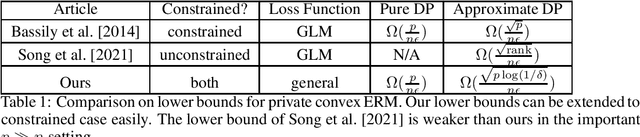
We consider the lower bounds of differentially private empirical risk minimization for general convex functions in this paper. For convex generalized linear models (GLMs), the well-known tight bound of DP-ERM in the constrained case is $\tilde{\Theta}(\frac{\sqrt{p}}{\epsilon n})$, while recently, \cite{sstt21} find the tight bound of DP-ERM in the unconstrained case is $\tilde{\Theta}(\frac{\sqrt{\text{rank}}}{\epsilon n})$ where $p$ is the dimension, $n$ is the sample size and $\text{rank}$ is the rank of the feature matrix of the GLM objective function. As $\text{rank}\leq \min\{n,p\}$, a natural and important question arises that whether we can evade the curse of dimensionality for over-parameterized models where $n\ll p$, for more general convex functions beyond GLM. We answer this question negatively by giving the first and tight lower bound of unconstrained private ERM for the general convex function, matching the current upper bound $\tilde{O}(\frac{\sqrt{p}}{n\epsilon})$ for unconstrained private ERM. We also give an $\Omega(\frac{p}{n\epsilon})$ lower bound for unconstrained pure-DP ERM which recovers the result in the constrained case.

Towards Certifying $\ell_\infty$ Robustness using Neural Networks with $\ell_\infty$-dist Neurons

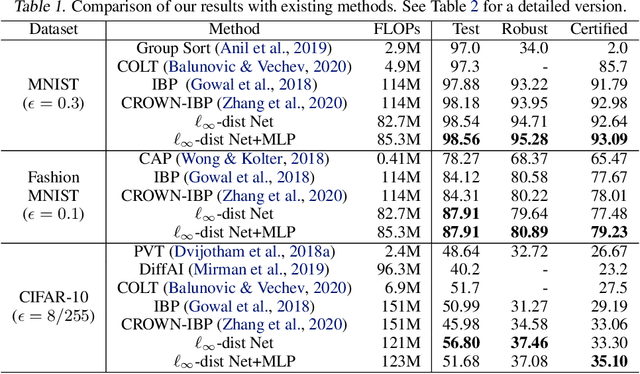
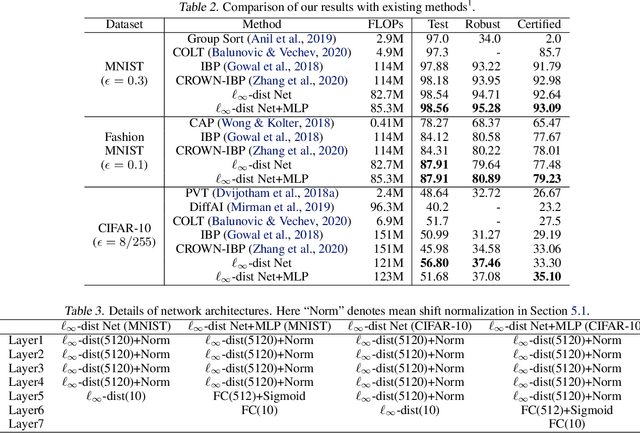
It is well-known that standard neural networks, even with a high classification accuracy, are vulnerable to small $\ell_\infty$-norm bounded adversarial perturbations. Although many attempts have been made, most previous works either can only provide empirical verification of the defense to a particular attack method, or can only develop a certified guarantee of the model robustness in limited scenarios. In this paper, we seek for a new approach to develop a theoretically principled neural network that inherently resists $\ell_\infty$ perturbations. In particular, we design a novel neuron that uses $\ell_\infty$-distance as its basic operation (which we call $\ell_\infty$-dist neuron), and show that any neural network constructed with $\ell_\infty$-dist neurons (called $\ell_{\infty}$-dist net) is naturally a 1-Lipschitz function with respect to $\ell_\infty$-norm. This directly provides a rigorous guarantee of the certified robustness based on the margin of prediction outputs. We also prove that such networks have enough expressive power to approximate any 1-Lipschitz function with robust generalization guarantee. Our experimental results show that the proposed network is promising. Using $\ell_{\infty}$-dist nets as the basic building blocks, we consistently achieve state-of-the-art performance on commonly used datasets: 93.09% certified accuracy on MNIST ($\epsilon=0.3$), 79.23% on Fashion MNIST ($\epsilon=0.1$) and 35.10% on CIFAR-10 ($\epsilon=8/255$).

A Note on the Representation Power of GHHs

In this note we prove a sharp lower bound on the necessary number of nestings of nested absolute-value functions of generalized hinging hyperplanes (GHH) to represent arbitrary CPWL functions. Previous upper bound states that $n+1$ nestings is sufficient for GHH to achieve universal representation power, but the corresponding lower bound was unknown. We prove that $n$ nestings is necessary for universal representation power, which provides an almost tight lower bound. We also show that one-hidden-layer neural networks don't have universal approximation power over the whole domain. The analysis is based on a key lemma showing that any finite sum of periodic functions is either non-integrable or the zero function, which might be of independent interest.

A Tight Lower Bound for Uniformly Stable Algorithms

Leveraging algorithmic stability to derive sharp generalization bounds is a classic and powerful approach in learning theory. Since Vapnik and Chervonenkis [1974] first formalized the idea for analyzing SVMs, it has been utilized to study many fundamental learning algorithms (e.g., $k$-nearest neighbors [Rogers and Wagner, 1978], stochastic gradient method [Hardt et al., 2016], linear regression [Maurer, 2017], etc). In a recent line of great works by Feldman and Vondrak [2018, 2019] as well as Bousquet et al. [2020b], they prove a high probability generalization upper bound of order $\tilde{\mathcal{O}}(\gamma +\frac{L}{\sqrt{n}})$ for any uniformly $\gamma$-stable algorithm and $L$-bounded loss function. Although much progress was achieved in proving generalization upper bounds for stable algorithms, our knowledge of lower bounds is rather limited. In fact, there is no nontrivial lower bound known ever since the study of uniform stability [Bousquet and Elisseeff, 2002], to the best of our knowledge. In this paper we fill the gap by proving a tight generalization lower bound of order $\Omega(\gamma+\frac{L}{\sqrt{n}})$, which matches the best known upper bound up to logarithmic factors

A Note on John Simplex with Positive Dilation

We prove a Johns theorem for simplices in $R^d$ with positive dilation factor $d+2$, which improves the previously known $d^2$ upper bound. This bound is tight in view of the $d$ lower bound. Furthermore, we give an example that $d$ isn't the optimal lower bound when $d=2$. Our results answered both questions regarding Johns theorem for simplices with positive dilation raised by \cite{leme2020costly}.