Zhenbang Wang
MANZANO: A Simple and Scalable Unified Multimodal Model with a Hybrid Vision Tokenizer
Sep 19, 2025
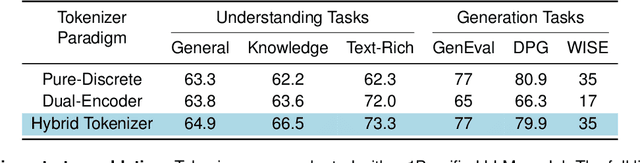
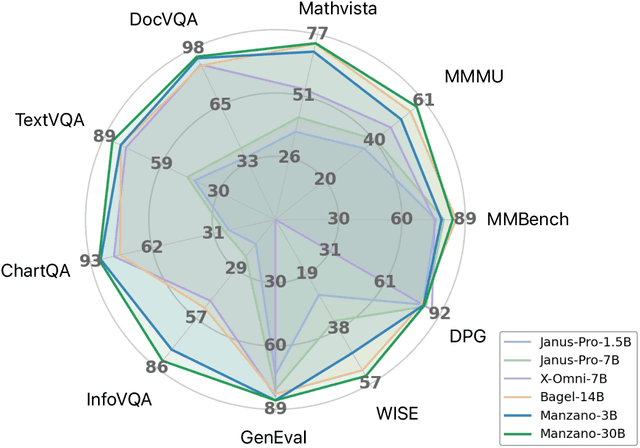
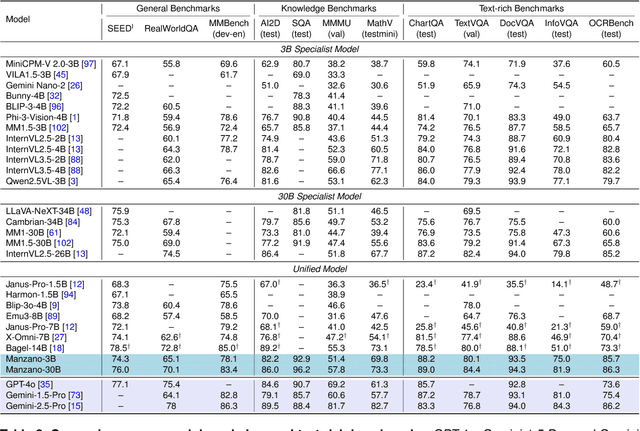
Abstract:Unified multimodal Large Language Models (LLMs) that can both understand and generate visual content hold immense potential. However, existing open-source models often suffer from a performance trade-off between these capabilities. We present Manzano, a simple and scalable unified framework that substantially reduces this tension by coupling a hybrid image tokenizer with a well-curated training recipe. A single shared vision encoder feeds two lightweight adapters that produce continuous embeddings for image-to-text understanding and discrete tokens for text-to-image generation within a common semantic space. A unified autoregressive LLM predicts high-level semantics in the form of text and image tokens, with an auxiliary diffusion decoder subsequently translating the image tokens into pixels. The architecture, together with a unified training recipe over understanding and generation data, enables scalable joint learning of both capabilities. Manzano achieves state-of-the-art results among unified models, and is competitive with specialist models, particularly on text-rich evaluation. Our studies show minimal task conflicts and consistent gains from scaling model size, validating our design choice of a hybrid tokenizer.
APTOS-2024 challenge report: Generation of synthetic 3D OCT images from fundus photographs
Jun 09, 2025Abstract:Optical Coherence Tomography (OCT) provides high-resolution, 3D, and non-invasive visualization of retinal layers in vivo, serving as a critical tool for lesion localization and disease diagnosis. However, its widespread adoption is limited by equipment costs and the need for specialized operators. In comparison, 2D color fundus photography offers faster acquisition and greater accessibility with less dependence on expensive devices. Although generative artificial intelligence has demonstrated promising results in medical image synthesis, translating 2D fundus images into 3D OCT images presents unique challenges due to inherent differences in data dimensionality and biological information between modalities. To advance generative models in the fundus-to-3D-OCT setting, the Asia Pacific Tele-Ophthalmology Society (APTOS-2024) organized a challenge titled Artificial Intelligence-based OCT Generation from Fundus Images. This paper details the challenge framework (referred to as APTOS-2024 Challenge), including: the benchmark dataset, evaluation methodology featuring two fidelity metrics-image-based distance (pixel-level OCT B-scan similarity) and video-based distance (semantic-level volumetric consistency), and analysis of top-performing solutions. The challenge attracted 342 participating teams, with 42 preliminary submissions and 9 finalists. Leading methodologies incorporated innovations in hybrid data preprocessing or augmentation (cross-modality collaborative paradigms), pre-training on external ophthalmic imaging datasets, integration of vision foundation models, and model architecture improvement. The APTOS-2024 Challenge is the first benchmark demonstrating the feasibility of fundus-to-3D-OCT synthesis as a potential solution for improving ophthalmic care accessibility in under-resourced healthcare settings, while helping to expedite medical research and clinical applications.
Regularization for Shuffled Data Problems via Exponential Family Priors on the Permutation Group
Nov 02, 2021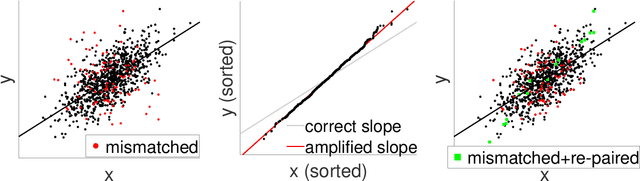
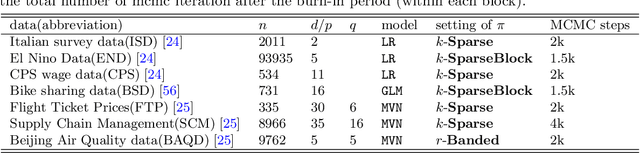
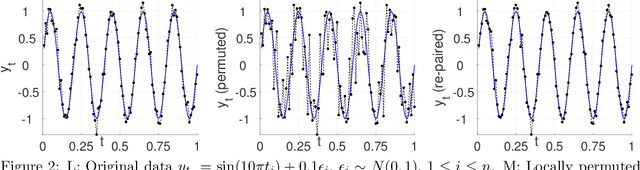
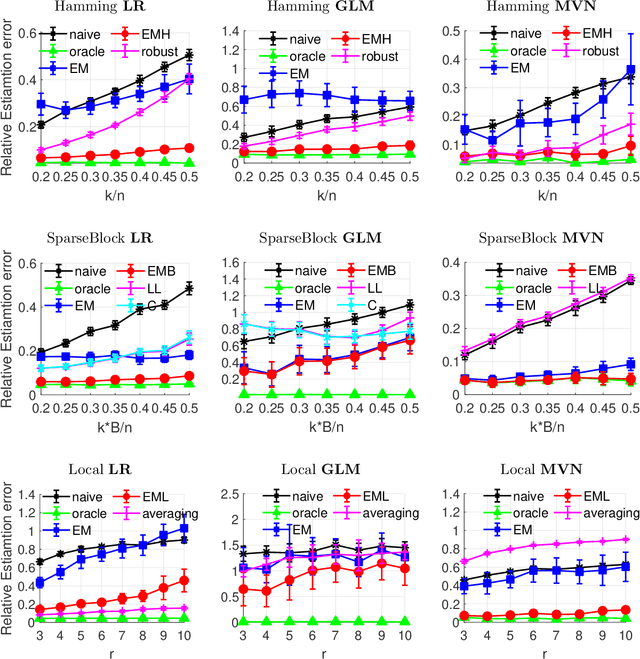
Abstract:In the analysis of data sets consisting of (X, Y)-pairs, a tacit assumption is that each pair corresponds to the same observation unit. If, however, such pairs are obtained via record linkage of two files, this assumption can be violated as a result of mismatch error rooting, for example, in the lack of reliable identifiers in the two files. Recently, there has been a surge of interest in this setting under the term "Shuffled data" in which the underlying correct pairing of (X, Y)-pairs is represented via an unknown index permutation. Explicit modeling of the permutation tends to be associated with substantial overfitting, prompting the need for suitable methods of regularization. In this paper, we propose a flexible exponential family prior on the permutation group for this purpose that can be used to integrate various structures such as sparse and locally constrained shuffling. This prior turns out to be conjugate for canonical shuffled data problems in which the likelihood conditional on a fixed permutation can be expressed as product over the corresponding (X,Y)-pairs. Inference is based on the EM algorithm in which the intractable E-step is approximated by the Fisher-Yates algorithm. The M-step is shown to admit a significant reduction from $n^2$ to $n$ terms if the likelihood of (X,Y)-pairs has exponential family form as in the case of generalized linear models. Comparisons on synthetic and real data show that the proposed approach compares favorably to competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge