Learning Generalizable Shape Completion with SIM(3) Equivariance

3D shape completion methods typically assume scans are pre-aligned to a canonical frame. This leaks pose and scale cues that networks may exploit to memorize absolute positions rather than inferring intrinsic geometry. When such alignment is absent in real data, performance collapses. We argue that robust generalization demands architectural equivariance to the similarity group, SIM(3), so the model remains agnostic to pose and scale. Following this principle, we introduce the first SIM(3)-equivariant shape completion network, whose modular layers successively canonicalize features, reason over similarity-invariant geometry, and restore the original frame. Under a de-biased evaluation protocol that removes the hidden cues, our model outperforms both equivariant and augmentation baselines on the PCN benchmark. It also sets new cross-domain records on real driving and indoor scans, lowering minimal matching distance on KITTI by 17% and Chamfer distance $\ell1$ on OmniObject3D by 14%. Perhaps surprisingly, ours under the stricter protocol still outperforms competitors under their biased settings. These results establish full SIM(3) equivariance as an effective route to truly generalizable shape completion. Project page: https://sime-completion.github.io.

TUM2TWIN: Introducing the Large-Scale Multimodal Urban Digital Twin Benchmark Dataset

Urban Digital Twins (UDTs) have become essential for managing cities and integrating complex, heterogeneous data from diverse sources. Creating UDTs involves challenges at multiple process stages, including acquiring accurate 3D source data, reconstructing high-fidelity 3D models, maintaining models' updates, and ensuring seamless interoperability to downstream tasks. Current datasets are usually limited to one part of the processing chain, hampering comprehensive UDTs validation. To address these challenges, we introduce the first comprehensive multimodal Urban Digital Twin benchmark dataset: TUM2TWIN. This dataset includes georeferenced, semantically aligned 3D models and networks along with various terrestrial, mobile, aerial, and satellite observations boasting 32 data subsets over roughly 100,000 $m^2$ and currently 767 GB of data. By ensuring georeferenced indoor-outdoor acquisition, high accuracy, and multimodal data integration, the benchmark supports robust analysis of sensors and the development of advanced reconstruction methods. Additionally, we explore downstream tasks demonstrating the potential of TUM2TWIN, including novel view synthesis of NeRF and Gaussian Splatting, solar potential analysis, point cloud semantic segmentation, and LoD3 building reconstruction. We are convinced this contribution lays a foundation for overcoming current limitations in UDT creation, fostering new research directions and practical solutions for smarter, data-driven urban environments. The project is available under: https://tum2t.win

Parametric Point Cloud Completion for Polygonal Surface Reconstruction

Existing polygonal surface reconstruction methods heavily depend on input completeness and struggle with incomplete point clouds. We argue that while current point cloud completion techniques may recover missing points, they are not optimized for polygonal surface reconstruction, where the parametric representation of underlying surfaces remains overlooked. To address this gap, we introduce parametric completion, a novel paradigm for point cloud completion, which recovers parametric primitives instead of individual points to convey high-level geometric structures. Our presented approach, PaCo, enables high-quality polygonal surface reconstruction by leveraging plane proxies that encapsulate both plane parameters and inlier points, proving particularly effective in challenging scenarios with highly incomplete data. Comprehensive evaluations of our approach on the ABC dataset establish its effectiveness with superior performance and set a new standard for polygonal surface reconstruction from incomplete data. Project page: https://parametric-completion.github.io.

Beyond Grid Data: Exploring Graph Neural Networks for Earth Observation

Earth Observation (EO) data analysis has been significantly revolutionized by deep learning (DL), with applications typically limited to grid-like data structures. Graph Neural Networks (GNNs) emerge as an important innovation, propelling DL into the non-Euclidean domain. Naturally, GNNs can effectively tackle the challenges posed by diverse modalities, multiple sensors, and the heterogeneous nature of EO data. To introduce GNNs in the related domains, our review begins by offering fundamental knowledge on GNNs. Then, we summarize the generic problems in EO, to which GNNs can offer potential solutions. Following this, we explore a broad spectrum of GNNs' applications to scientific problems in Earth systems, covering areas such as weather and climate analysis, disaster management, air quality monitoring, agriculture, land cover classification, hydrological process modeling, and urban modeling. The rationale behind adopting GNNs in these fields is explained, alongside methodologies for organizing graphs and designing favorable architectures for various tasks. Furthermore, we highlight methodological challenges of implementing GNNs in these domains and possible solutions that could guide future research. While acknowledging that GNNs are not a universal solution, we conclude the paper by comparing them with other popular architectures like transformers and analyzing their potential synergies.

PolyGNN: Polyhedron-based Graph Neural Network for 3D Building Reconstruction from Point Clouds

We present PolyGNN, a polyhedron-based graph neural network for 3D building reconstruction from point clouds. PolyGNN learns to assemble primitives obtained by polyhedral decomposition via graph node classification, achieving a watertight, compact, and weakly semantic reconstruction. To effectively represent arbitrary-shaped polyhedra in the neural network, we propose three different sampling strategies to select representative points as polyhedron-wise queries, enabling efficient occupancy inference. Furthermore, we incorporate the inter-polyhedron adjacency to enhance the classification of the graph nodes. We also observe that existing city-building models are abstractions of the underlying instances. To address this abstraction gap and provide a fair evaluation of the proposed method, we develop our method on a large-scale synthetic dataset covering 500k+ buildings with well-defined ground truths of polyhedral class labels. We further conduct a transferability analysis across cities and on real-world point clouds. Both qualitative and quantitative results demonstrate the effectiveness of our method, particularly its efficiency for large-scale reconstructions. The source code and data of our work are available at https://github.com/chenzhaiyu/polygnn.

Reconstructing Compact Building Models from Point Clouds Using Deep Implicit Fields

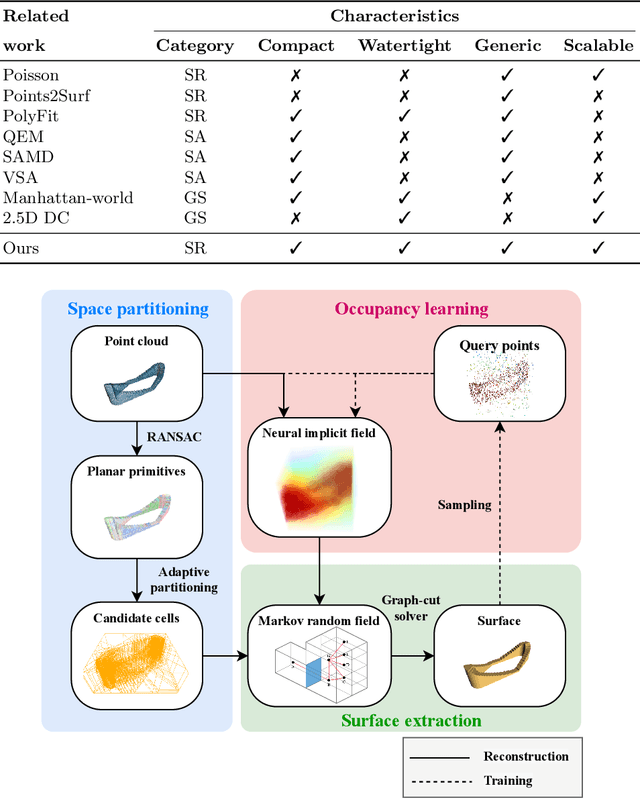
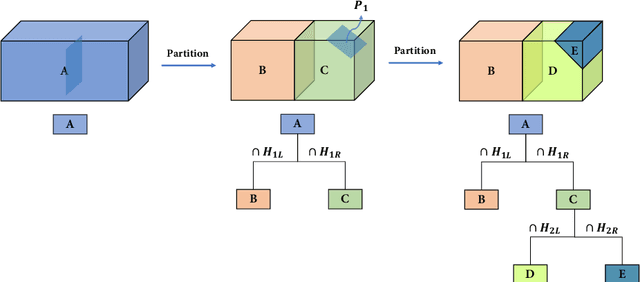
Three-dimensional (3D) building models play an increasingly pivotal role in many real-world applications while obtaining a compact representation of buildings remains an open problem. In this paper, we present a novel framework for reconstructing compact, watertight, polygonal building models from point clouds. Our framework comprises three components: (a) a cell complex is generated via adaptive space partitioning that provides a polyhedral embedding as the candidate set; (b) an implicit field is learned by a deep neural network that facilitates building occupancy estimation; (c) a Markov random field is formulated to extract the outer surface of a building via combinatorial optimization. We evaluate and compare our method with state-of-the-art methods in shape reconstruction, surface approximation, and geometry simplification. Experiments on both synthetic and real-world point clouds have demonstrated that, with our neural-guided strategy, high-quality building models can be obtained with significant advantages in fidelity, compactness, and computational efficiency. Our method shows robustness to noise and insufficient measurements, and it can directly generalize from synthetic scans to real-world measurements. The source code of this work is freely available at https://github.com/chenzhaiyu/points2poly.