Manifold Proximal Point Algorithms for Dual Principal Component Pursuit and Orthogonal Dictionary Learning

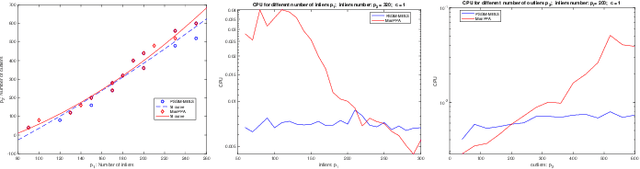
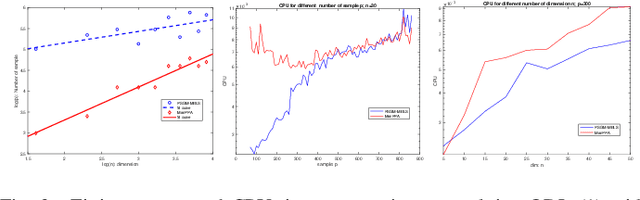
We consider the problem of maximizing the $\ell_1$ norm of a linear map over the sphere, which arises in various machine learning applications such as orthogonal dictionary learning (ODL) and robust subspace recovery (RSR). The problem is numerically challenging due to its nonsmooth objective and nonconvex constraint, and its algorithmic aspects have not been well explored. In this paper, we show how the manifold structure of the sphere can be exploited to design fast algorithms for tackling this problem. Specifically, our contribution is threefold. First, we present a manifold proximal point algorithm (ManPPA) for the problem and show that it converges at a sublinear rate. Furthermore, we show that ManPPA can achieve a quadratic convergence rate when applied to the ODL and RSR problems. Second, we propose a stochastic variant of ManPPA called StManPPA, which is well suited for large-scale computation, and establish its sublinear convergence rate. Both ManPPA and StManPPA have provably faster convergence rates than existing subgradient-type methods. Third, using ManPPA as a building block, we propose a new approach to solving a matrix analog of the problem, in which the sphere is replaced by the Stiefel manifold. The results from our extensive numerical experiments on the ODL and RSR problems demonstrate the efficiency and efficacy of our proposed methods.

Nonsmooth Optimization over Stiefel Manifold: Riemannian Subgradient Methods

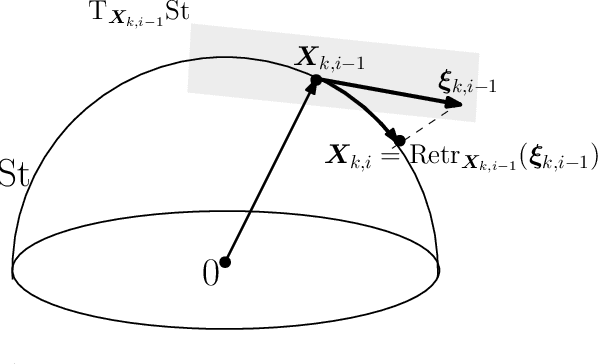
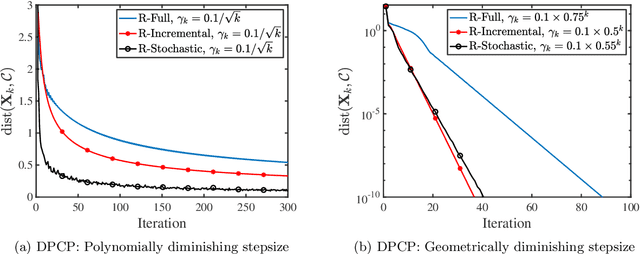
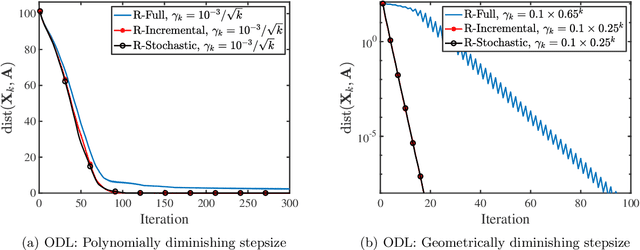
We consider a class of nonsmooth optimization problems over Stefiel manifold, which are ubiquitous in engineering applications but still largely unexplored. We study this type of nonconvex optimization problems under the settings that the function is weakly convex in Euclidean space and locally Lipschitz continuous, where we propose to address these problems using a family of Riemannian subgradient methods. First, we show iteration complexity ${\cal O}(\varepsilon^{-4})$ for these algorithms driving a natural stationary measure to be smaller than $\varepsilon$. Moreover, local linear convergence can be achieved for Riemannian subgradient and incremental subgradient methods if the optimization problem further satisfies the sharpness property and the algorithms are initialized close to the set of weak sharp minima. As a result, we provide the first convergence rate guarantees for a family of Riemannian subgradient methods utilized to optimize nonsmooth functions over Stiefel manifold, under reasonable regularities of the functions. The fundamental ingredient for establishing the aforementioned convergence results is that any weakly convex function in Euclidean space admits an important property holding uniformly over Stiefel manifold which we name Riemannian subgradient inequality. We then extend our convergence results to a broader class of compact Riemannian manifolds embedded in Euclidean space. Finally, we discuss the sharpness property for robust subspace recovery and orthogonal dictionary learning, and demonstrate the established convergence performance of our algorithms on both problems via numerical simulations.

Voting-Based Multi-Agent Reinforcement Learning

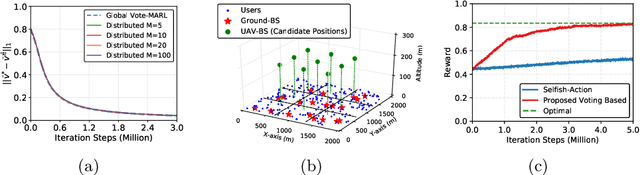
The recent success of single-agent reinforcement learning (RL) encourages the exploration of multi-agent reinforcement learning (MARL), which is more challenging due to the interactions among different agents. In this paper, we consider a voting-based MARL problem, in which the agents vote to make group decisions and the goal is to maximize the globally averaged returns. To this end, we formulate the MARL problem based on the linear programming form of the policy optimization problem and propose a distributed primal-dual algorithm to obtain the optimal solution. We also propose a voting mechanism through which the distributed learning achieves the same sub-linear convergence rate as centralized learning. In other words, the distributed decision making does not slow down the global consensus to optimal. We also verify the convergence of our proposed algorithm with numerical simulations and conduct case studies in practical multi-agent systems.

An Efficient Augmented Lagrangian Based Method for Constrained Lasso

Variable selection is one of the most important tasks in statistics and machine learning. To incorporate more prior information about the regression coefficients, the constrained Lasso model has been proposed in the literature. In this paper, we present an inexact augmented Lagrangian method to solve the Lasso problem with linear equality constraints. By fully exploiting second-order sparsity of the problem, we are able to greatly reduce the computational cost and obtain highly efficient implementations. Furthermore, numerical results on both synthetic data and real data show that our algorithm is superior to existing first-order methods in terms of both running time and solution accuracy.