Nonsmooth Optimization over Stiefel Manifold: Riemannian Subgradient Methods

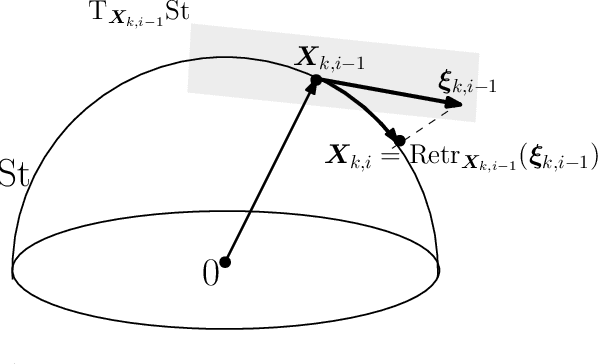
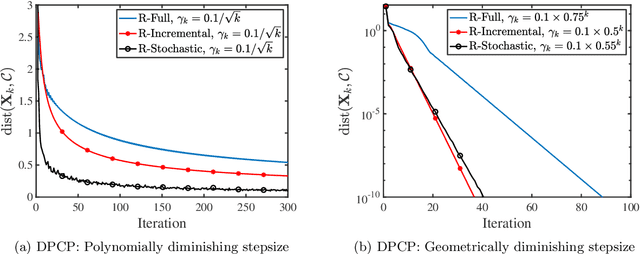
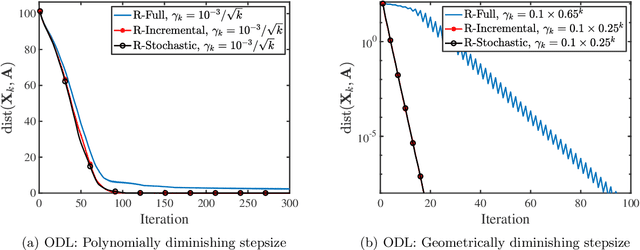
We consider a class of nonsmooth optimization problems over Stefiel manifold, which are ubiquitous in engineering applications but still largely unexplored. We study this type of nonconvex optimization problems under the settings that the function is weakly convex in Euclidean space and locally Lipschitz continuous, where we propose to address these problems using a family of Riemannian subgradient methods. First, we show iteration complexity ${\cal O}(\varepsilon^{-4})$ for these algorithms driving a natural stationary measure to be smaller than $\varepsilon$. Moreover, local linear convergence can be achieved for Riemannian subgradient and incremental subgradient methods if the optimization problem further satisfies the sharpness property and the algorithms are initialized close to the set of weak sharp minima. As a result, we provide the first convergence rate guarantees for a family of Riemannian subgradient methods utilized to optimize nonsmooth functions over Stiefel manifold, under reasonable regularities of the functions. The fundamental ingredient for establishing the aforementioned convergence results is that any weakly convex function in Euclidean space admits an important property holding uniformly over Stiefel manifold which we name Riemannian subgradient inequality. We then extend our convergence results to a broader class of compact Riemannian manifolds embedded in Euclidean space. Finally, we discuss the sharpness property for robust subspace recovery and orthogonal dictionary learning, and demonstrate the established convergence performance of our algorithms on both problems via numerical simulations.