A Taylor Series Approach to Correction of Input Errors in Gaussian Process Regression

Gaussian Processes (GPs) are widely recognized as powerful non-parametric models for regression and classification. Traditional GP frameworks predominantly operate under the assumption that the inputs are either accurately known or subject to zero-mean noise. However, several real-world applications such as mobile sensors have imperfect localization, leading to inputs with biased errors. These biases can typically be estimated through measurements collected over time using, for example, Kalman filters. To avoid recomputation of the entire GP model when better estimates of the inputs used in the training data become available, we introduce a technique for updating a trained GP model to incorporate updated estimates of the inputs. By leveraging the differentiability of the mean and covariance functions derived from the squared exponential kernel, a second-order correction algorithm is developed to update the trained GP models. Precomputed Jacobians and Hessians of kernels enable real-time refinement of the mean and covariance predictions. The efficacy of the developed approach is demonstrated using two simulation studies, with error analyses revealing improvements in both predictive accuracy and uncertainty quantification.

Improved Dwell-times for Switched Nonlinear Systems using Memory Regression Extension

This paper presents a switched systems approach for extending the dwell-time of an autonomous agent during GPS-denied operation by leveraging memory regressor extension (MRE) techniques. To maintain accurate trajectory tracking despite unknown dynamics and environmental disturbances, the agent periodically acquires access to GPS, allowing it to correct accumulated state estimation errors. The motivation for this work arises from the limitations of existing switched system approaches, where increasing estimation errors during GPS-denied intervals and overly conservative dwell-time conditions restrict the operational efficiency of the agent. By leveraging MRE techniques during GPS-available intervals, the developed method refines the estimates of unknown system parameters, thereby enabling longer and more reliable operation in GPS-denied environments. A Lyapunov-based switched-system stability analysis establishes that improved parameter estimates obtained through concurrent learning allow extended operation in GPS-denied intervals without compromising closed-loop system stability. Simulation results validate the theoretical findings, demonstrating dwell-time extensions and enhanced trajectory tracking performance.

A Zeroth-Order Momentum Method for Risk-Averse Online Convex Games

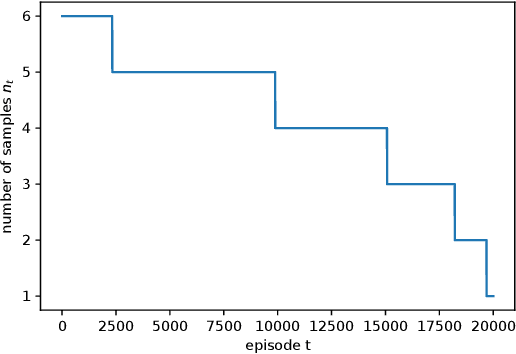
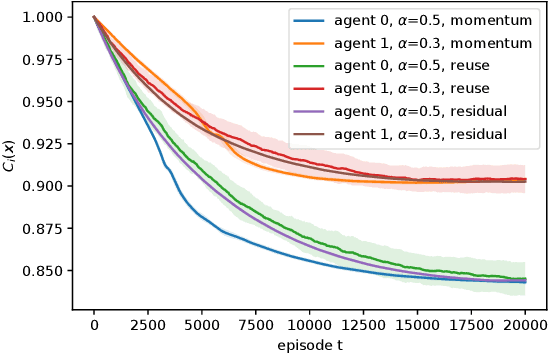
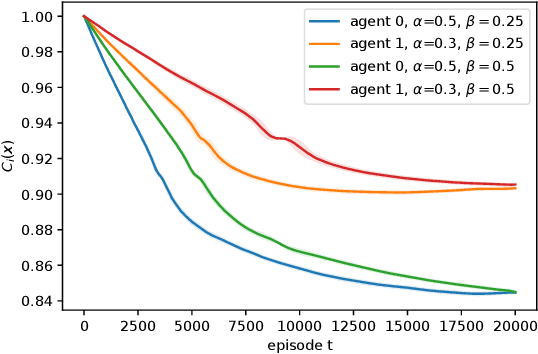
We consider risk-averse learning in repeated unknown games where the goal of the agents is to minimize their individual risk of incurring significantly high cost. Specifically, the agents use the conditional value at risk (CVaR) as a risk measure and rely on bandit feedback in the form of the cost values of the selected actions at every episode to estimate their CVaR values and update their actions. A major challenge in using bandit feedback to estimate CVaR is that the agents can only access their own cost values, which, however, depend on the actions of all agents. To address this challenge, we propose a new risk-averse learning algorithm with momentum that utilizes the full historical information on the cost values. We show that this algorithm achieves sub-linear regret and matches the best known algorithms in the literature. We provide numerical experiments for a Cournot game that show that our method outperforms existing methods.