Analyzing and Improving Diffusion Models for Time-Series Data Imputation: A Proximal Recursion Perspective

Diffusion models (DMs) have shown promise for Time-Series Data Imputation (TSDI); however, their performance remains inconsistent in complex scenarios. We attribute this to two primary obstacles: (1) non-stationary temporal dynamics, which can bias the inference trajectory and lead to outlier-sensitive imputations; and (2) objective inconsistency, since imputation favors accurate pointwise recovery whereas DMs are inherently trained to generate diverse samples. To better understand these issues, we analyze DM-based TSDI process through a proximal-operator perspective and uncover that an implicit Wasserstein distance regularization inherent in the process hinders the model's ability to counteract non-stationarity and dissipative regularizer, thereby amplifying diversity at the expense of fidelity. Building on this insight, we propose a novel framework called SPIRIT (Semi-Proximal Transport Regularized time-series Imputation). Specifically, we introduce entropy-induced Bregman divergence to relax the mass preserving constraint in the Wasserstein distance, formulate the semi-proximal transport (SPT) discrepancy, and theoretically prove the robustness of SPT against non-stationarity. Subsequently, we remove the dissipative structure and derive the complete SPIRIT workflow, with SPT serving as the proximal operator. Extensive experiments demonstrate the effectiveness of the proposed SPIRIT approach.

Rethinking the Flow-Based Gradual Domain Adaption: A Semi-Dual Optimal Transport Perspective

Gradual domain adaptation (GDA) aims to mitigate domain shift by progressively adapting models from the source domain to the target domain via intermediate domains. However, real intermediate domains are often unavailable or ineffective, necessitating the synthesis of intermediate samples. Flow-based models have recently been used for this purpose by interpolating between source and target distributions; however, their training typically relies on sample-based log-likelihood estimation, which can discard useful information and thus degrade GDA performance. The key to addressing this limitation is constructing the intermediate domains via samples directly. To this end, we propose an Entropy-regularized Semi-dual Unbalanced Optimal Transport (E-SUOT) framework to construct intermediate domains. Specifically, we reformulate flow-based GDA as a Lagrangian dual problem and derive an equivalent semi-dual objective that circumvents the need for likelihood estimation. However, the dual problem leads to an unstable min-max training procedure. To alleviate this issue, we further introduce entropy regularization to convert it into a more stable alternative optimization procedure. Based on this, we propose a novel GDA training framework and provide theoretical analysis in terms of stability and generalization. Finally, extensive experiments are conducted to demonstrate the efficacy of the E-SUOT framework.

AutoDrop: Training Deep Learning Models with Automatic Learning Rate Drop

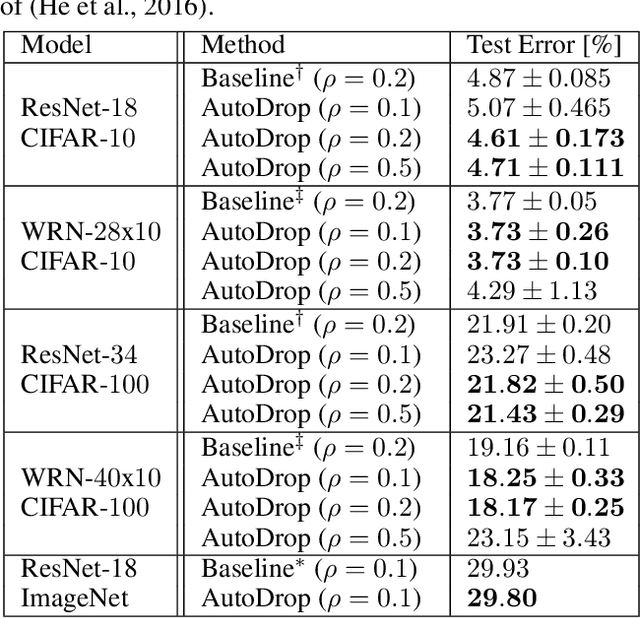
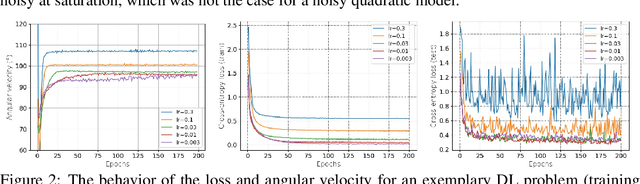
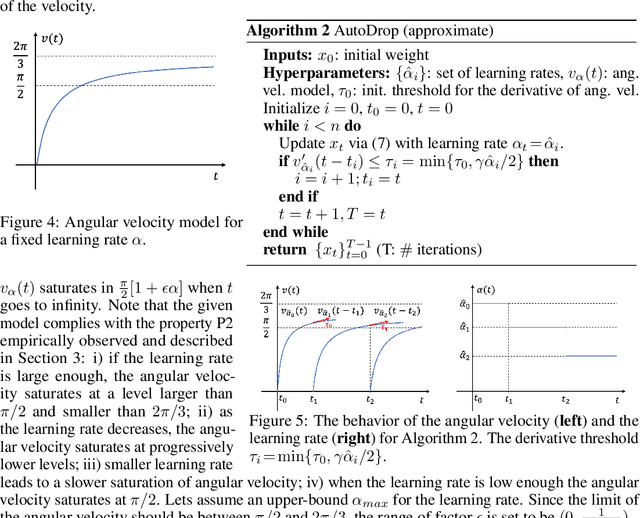
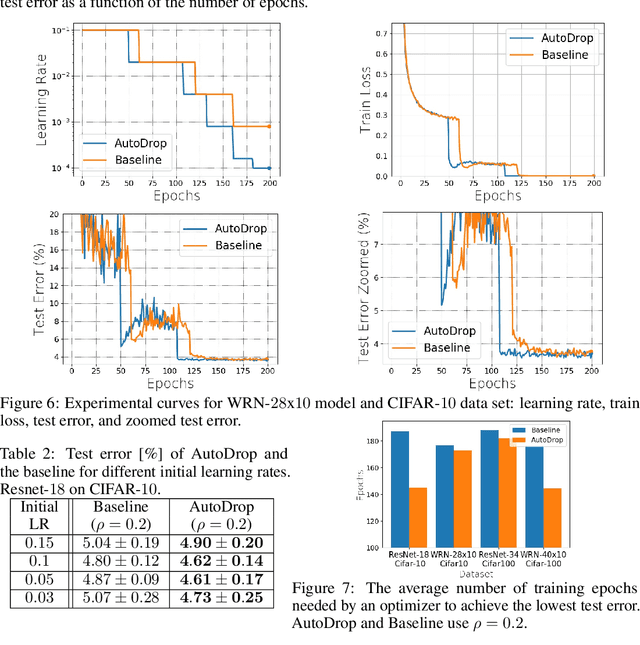
Modern deep learning (DL) architectures are trained using variants of the SGD algorithm that is run with a $\textit{manually}$ defined learning rate schedule, i.e., the learning rate is dropped at the pre-defined epochs, typically when the training loss is expected to saturate. In this paper we develop an algorithm that realizes the learning rate drop $\textit{automatically}$. The proposed method, that we refer to as AutoDrop, is motivated by the observation that the angular velocity of the model parameters, i.e., the velocity of the changes of the convergence direction, for a fixed learning rate initially increases rapidly and then progresses towards soft saturation. At saturation the optimizer slows down thus the angular velocity saturation is a good indicator for dropping the learning rate. After the drop, the angular velocity "resets" and follows the previously described pattern - it increases again until saturation. We show that our method improves over SOTA training approaches: it accelerates the training of DL models and leads to a better generalization. We also show that our method does not require any extra hyperparameter tuning. AutoDrop is furthermore extremely simple to implement and computationally cheap. Finally, we develop a theoretical framework for analyzing our algorithm and provide convergence guarantees.

Continual learning with direction-constrained optimization

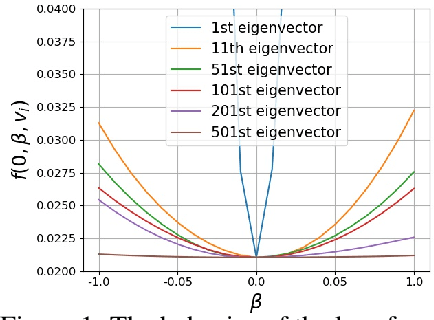
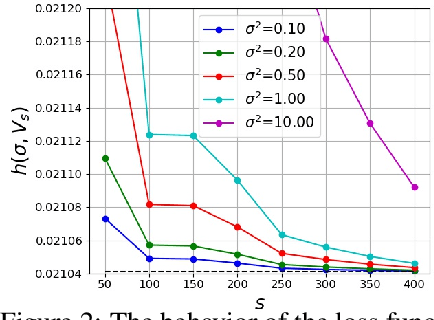
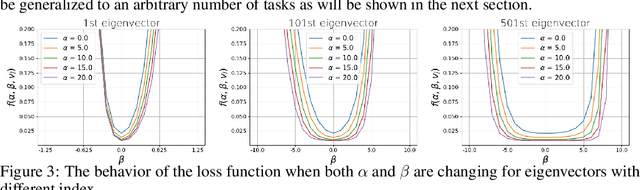
This paper studies a new design of the optimization algorithm for training deep learning models with a fixed architecture of the classification network in a continual learning framework, where the training data is non-stationary and the non-stationarity is imposed by a sequence of distinct tasks. This setting implies the existence of a manifold of network parameters that correspond to good performance of the network on all tasks. Our algorithm is derived from the geometrical properties of this manifold. We first analyze a deep model trained on only one learning task in isolation and identify a region in network parameter space, where the model performance is close to the recovered optimum. We provide empirical evidence that this region resembles a cone that expands along the convergence direction. We study the principal directions of the trajectory of the optimizer after convergence and show that traveling along a few top principal directions can quickly bring the parameters outside the cone but this is not the case for the remaining directions. We argue that catastrophic forgetting in a continual learning setting can be alleviated when the parameters are constrained to stay within the intersection of the plausible cones of individual tasks that were so far encountered during training. Enforcing this is equivalent to preventing the parameters from moving along the top principal directions of convergence corresponding to the past tasks. For each task we introduce a new linear autoencoder to approximate its corresponding top forbidden principal directions. They are then incorporated into the loss function in the form of a regularization term for the purpose of learning the coming tasks without forgetting. We empirically demonstrate that our algorithm performs favorably compared to other state-of-art regularization-based continual learning methods, including EWC and SI.

Leader Stochastic Gradient Descent for Distributed Training of Deep Learning Models

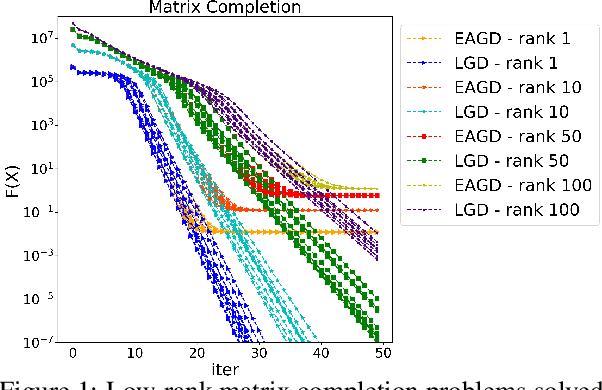
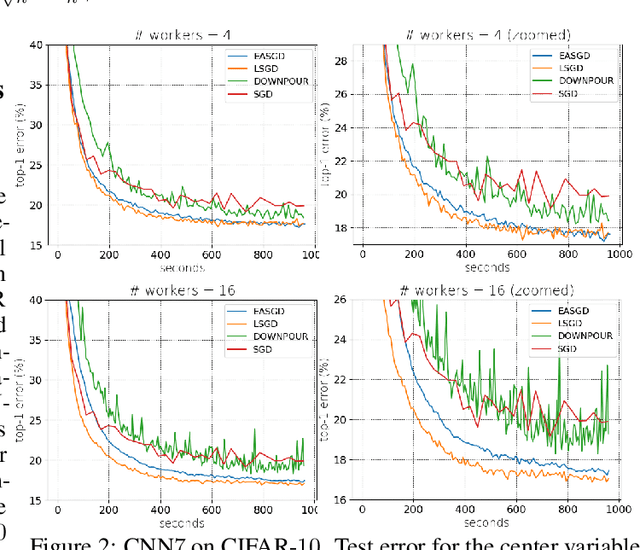
We consider distributed optimization under communication constraints for training deep learning models. We propose a new algorithm, whose parameter updates rely on two forces: a regular gradient step, and a corrective direction dictated by the currently best-performing worker (leader). Our method differs from the parameter-averaging scheme EASGD in a number of ways: (i) our objective formulation does not change the location of stationary points compared to the original optimization problem; (ii) we avoid convergence decelerations caused by pulling local workers descending to different local minima to each other (i.e. to the average of their parameters); (iii) our update by design breaks the curse of symmetry (the phenomenon of being trapped in poorly generalizing sub-optimal solutions in symmetric non-convex landscapes); and (iv) our approach is more communication efficient since it broadcasts only parameters of the leader rather than all workers. We provide theoretical analysis of the batch version of the proposed algorithm, which we call Leader Gradient Descent (LGD), and its stochastic variant (LSGD). Finally, we implement an asynchronous version of our algorithm and extend it to the multi-leader setting, where we form groups of workers, each represented by its own local leader (the best performer in a group), and update each worker with a corrective direction comprised of two attractive forces: one to the local, and one to the global leader (the best performer among all workers). The multi-leader setting is well-aligned with current hardware architecture, where local workers forming a group lie within a single computational node and different groups correspond to different nodes. For training convolutional neural networks, we empirically demonstrate that our approach compares favorably to state-of-the-art baselines.

Invertible Autoencoder for domain adaptation

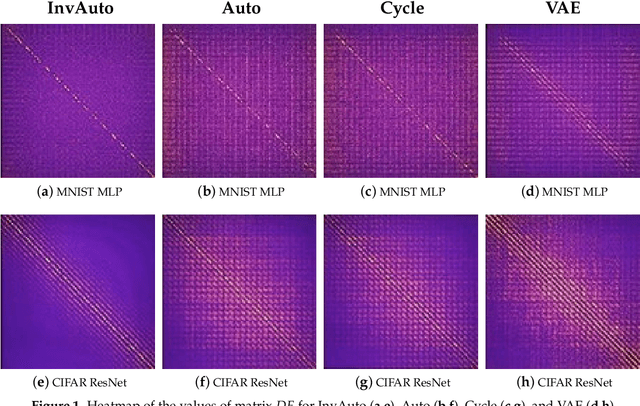
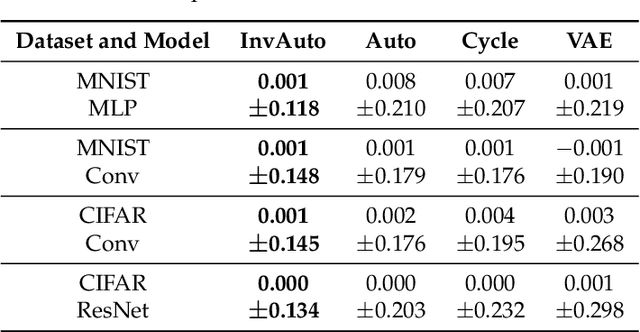
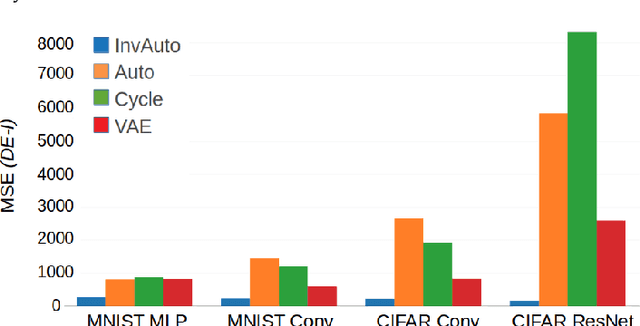
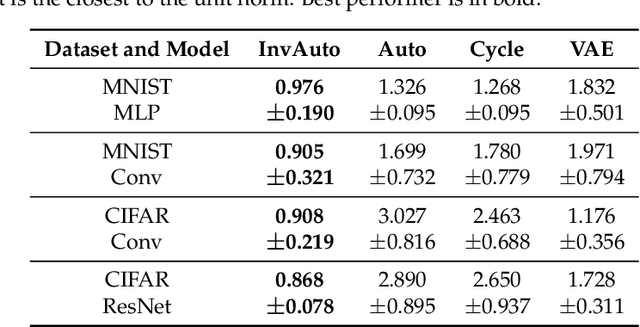
The unsupervised image-to-image translation aims at finding a mapping between the source ($A$) and target ($B$) image domains, where in many applications aligned image pairs are not available at training. This is an ill-posed learning problem since it requires inferring the joint probability distribution from marginals. Joint learning of coupled mappings $F_{AB}: A \rightarrow B$ and $F_{BA}: B \rightarrow A$ is commonly used by the state-of-the-art methods, like CycleGAN [Zhu et al., 2017], to learn this translation by introducing cycle consistency requirement to the learning problem, i.e. $F_{AB}(F_{BA}(B)) \approx B$ and $F_{BA}(F_{AB}(A)) \approx A$. Cycle consistency enforces the preservation of the mutual information between input and translated images. However, it does not explicitly enforce $F_{BA}$ to be an inverse operation to $F_{AB}$. We propose a new deep architecture that we call invertible autoencoder (InvAuto) to explicitly enforce this relation. This is done by forcing an encoder to be an inverted version of the decoder, where corresponding layers perform opposite mappings and share parameters. The mappings are constrained to be orthonormal. The resulting architecture leads to the reduction of the number of trainable parameters (up to $2$ times). We present image translation results on benchmark data sets and demonstrate state-of-the art performance of our approach. Finally, we test the proposed domain adaptation method on the task of road video conversion. We demonstrate that the videos converted with InvAuto have high quality and show that the NVIDIA neural-network-based end-to-end learning system for autonomous driving, known as PilotNet, trained on real road videos performs well when tested on the converted ones.