Provable Advantage of Parameterized Quantum Circuit in Function Approximation

Understanding the power of parameterized quantum circuits (PQCs) in accomplishing machine learning tasks is one of the most important questions in quantum machine learning. In this paper, we analyze the expressivity of PQCs through the lens of function approximation. Previously established universal approximation theorems for PQCs are mainly nonconstructive, leading us to the following question: How large do the PQCs need to be to approximate the target function up to a given error? We exhibit explicit constructions of data re-uploading PQCs for approximating continuous and smooth functions and establish quantitative approximation error bounds in terms of the width, the depth and the number of trainable parameters of the PQCs. To achieve this, we utilize techniques from quantum signal processing and linear combinations of unitaries to construct PQCs that implement multivariate polynomials. We implement global and local approximation techniques using Bernstein polynomials and local Taylor expansion and analyze their performances in the quantum setting. We also compare our proposed PQCs to nearly optimal deep neural networks in approximating high-dimensional smooth functions, showing that the ratio between model sizes of PQC and deep neural networks is exponentially small with respect to the input dimension. This suggests a potentially novel avenue for showcasing quantum advantages in quantum machine learning.

Non-Asymptotic Bounds for Adversarial Excess Risk under Misspecified Models

We propose a general approach to evaluating the performance of robust estimators based on adversarial losses under misspecified models. We first show that adversarial risk is equivalent to the risk induced by a distributional adversarial attack under certain smoothness conditions. This ensures that the adversarial training procedure is well-defined. To evaluate the generalization performance of the adversarial estimator, we study the adversarial excess risk. Our proposed analysis method includes investigations on both generalization error and approximation error. We then establish non-asymptotic upper bounds for the adversarial excess risk associated with Lipschitz loss functions. In addition, we apply our general results to adversarial training for classification and regression problems. For the quadratic loss in nonparametric regression, we show that the adversarial excess risk bound can be improved over those for a general loss.

Current density impedance imaging with PINNs

In this paper, we introduce CDII-PINNs, a computationally efficient method for solving CDII using PINNs in the framework of Tikhonov regularization. This method constructs a physics-informed loss function by merging the regularized least-squares output functional with an underlying differential equation, which describes the relationship between the conductivity and voltage. A pair of neural networks representing the conductivity and voltage, respectively, are coupled by this loss function. Then, minimizing the loss function provides a reconstruction. A rigorous theoretical guarantee is provided. We give an error analysis for CDII-PINNs and establish a convergence rate, based on prior selected neural network parameters in terms of the number of samples. The numerical simulations demonstrate that CDII-PINNs are efficient, accurate and robust to noise levels ranging from $1\%$ to $20\%$.

Differentiable Neural Networks with RePU Activation: with Applications to Score Estimation and Isotonic Regression

We study the properties of differentiable neural networks activated by rectified power unit (RePU) functions. We show that the partial derivatives of RePU neural networks can be represented by RePUs mixed-activated networks and derive upper bounds for the complexity of the function class of derivatives of RePUs networks. We establish error bounds for simultaneously approximating $C^s$ smooth functions and their derivatives using RePU-activated deep neural networks. Furthermore, we derive improved approximation error bounds when data has an approximate low-dimensional support, demonstrating the ability of RePU networks to mitigate the curse of dimensionality. To illustrate the usefulness of our results, we consider a deep score matching estimator (DSME) and propose a penalized deep isotonic regression (PDIR) using RePU networks. We establish non-asymptotic excess risk bounds for DSME and PDIR under the assumption that the target functions belong to a class of $C^s$ smooth functions. We also show that PDIR has a robustness property in the sense it is consistent with vanishing penalty parameters even when the monotonicity assumption is not satisfied. Furthermore, if the data distribution is supported on an approximate low-dimensional manifold, we show that DSME and PDIR can mitigate the curse of dimensionality.

GAS: A Gaussian Mixture Distribution-Based Adaptive Sampling Method for PINNs

With the recent study of deep learning in scientific computation, the Physics-Informed Neural Networks (PINNs) method has drawn widespread attention for solving Partial Differential Equations (PDEs). Compared to traditional methods, PINNs can efficiently handle high-dimensional problems, but the accuracy is relatively low, especially for highly irregular problems. Inspired by the idea of adaptive finite element methods and incremental learning, we propose GAS, a Gaussian mixture distribution-based adaptive sampling method for PINNs. During the training procedure, GAS uses the current residual information to generate a Gaussian mixture distribution for the sampling of additional points, which are then trained together with historical data to speed up the convergence of the loss and achieve higher accuracy. Several numerical simulations on 2D and 10D problems show that GAS is a promising method that achieves state-of-the-art accuracy among deep solvers, while being comparable with traditional numerical solvers.

Convergence Analysis of the Deep Galerkin Method for Weak Solutions

This paper analyzes the convergence rate of a deep Galerkin method for the weak solution (DGMW) of second-order elliptic partial differential equations on $\mathbb{R}^d$ with Dirichlet, Neumann, and Robin boundary conditions, respectively. In DGMW, a deep neural network is applied to parametrize the PDE solution, and a second neural network is adopted to parametrize the test function in the traditional Galerkin formulation. By properly choosing the depth and width of these two networks in terms of the number of training samples $n$, it is shown that the convergence rate of DGMW is $\mathcal{O}(n^{-1/d})$, which is the first convergence result for weak solutions. The main idea of the proof is to divide the error of the DGMW into an approximation error and a statistical error. We derive an upper bound on the approximation error in the $H^{1}$ norm and bound the statistical error via Rademacher complexity.

Estimation of Non-Crossing Quantile Regression Process with Deep ReQU Neural Networks

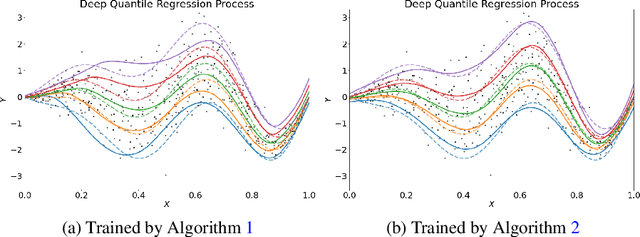
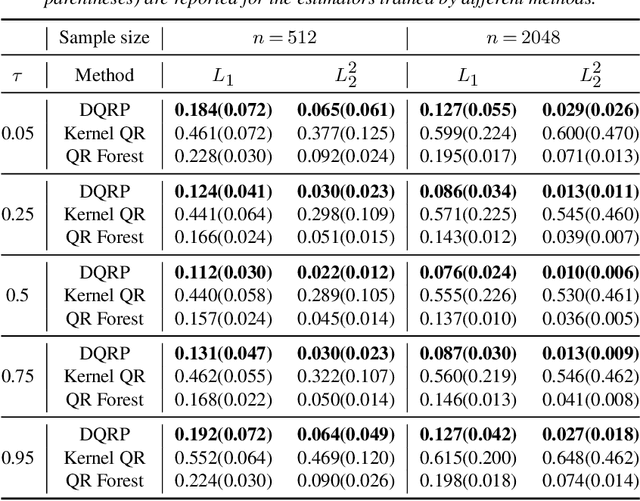
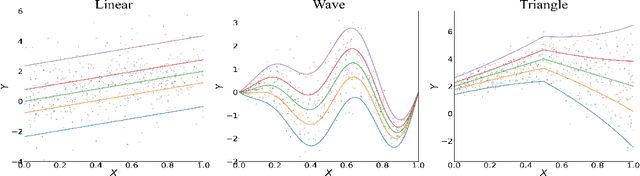
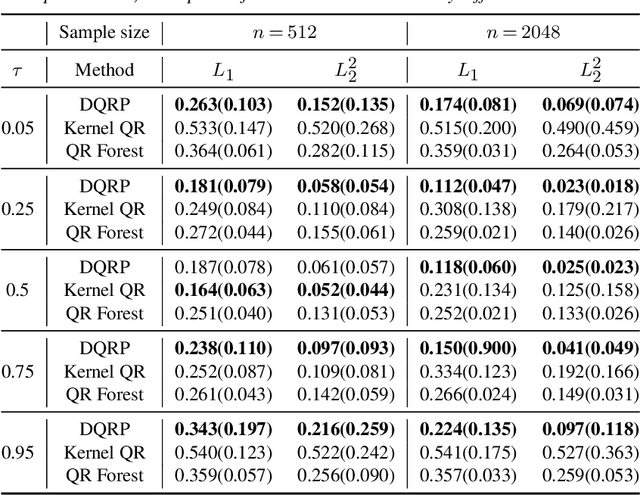
We propose a penalized nonparametric approach to estimating the quantile regression process (QRP) in a nonseparable model using rectifier quadratic unit (ReQU) activated deep neural networks and introduce a novel penalty function to enforce non-crossing of quantile regression curves. We establish the non-asymptotic excess risk bounds for the estimated QRP and derive the mean integrated squared error for the estimated QRP under mild smoothness and regularity conditions. To establish these non-asymptotic risk and estimation error bounds, we also develop a new error bound for approximating $C^s$ smooth functions with $s >0$ and their derivatives using ReQU activated neural networks. This is a new approximation result for ReQU networks and is of independent interest and may be useful in other problems. Our numerical experiments demonstrate that the proposed method is competitive with or outperforms two existing methods, including methods using reproducing kernels and random forests, for nonparametric quantile regression.

Efficient and practical quantum compiler towards multi-qubit systems with deep reinforcement learning

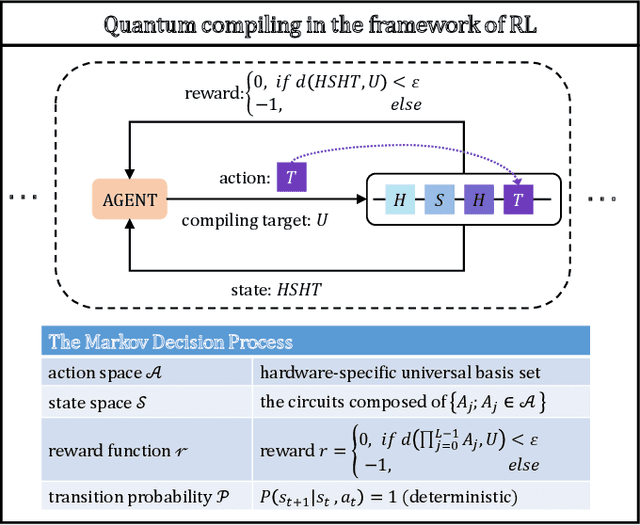
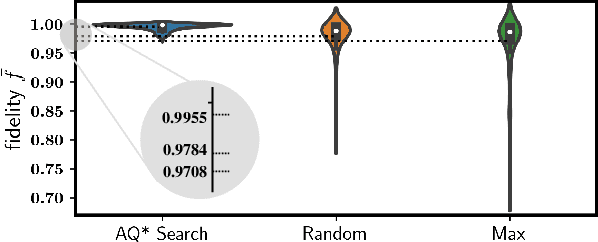
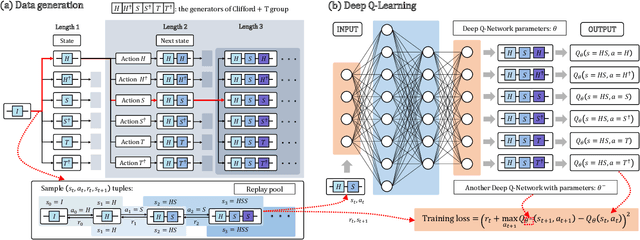
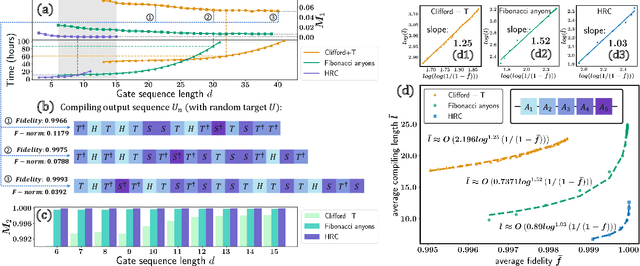
Efficient quantum compiling tactics greatly enhance the capability of quantum computers to execute complicated quantum algorithms. Due to its fundamental importance, a plethora of quantum compilers has been designed in past years. However, there are several caveats to current protocols, which are low optimality, high inference time, limited scalability, and lack of universality. To compensate for these defects, here we devise an efficient and practical quantum compiler assisted by advanced deep reinforcement learning (RL) techniques, i.e., data generation, deep Q-learning, and AQ* search. In this way, our protocol is compatible with various quantum machines and can be used to compile multi-qubit operators. We systematically evaluate the performance of our proposal in compiling quantum operators with both inverse-closed and inverse-free universal basis sets. In the task of single-qubit operator compiling, our proposal outperforms other RL-based quantum compilers in the measure of compiling sequence length and inference time. Meanwhile, the output solution is near-optimal, guaranteed by the Solovay-Kitaev theorem. Notably, for the inverse-free universal basis set, the achieved sequence length complexity is comparable with the inverse-based setting and dramatically advances previous methods. These empirical results contribute to improving the inverse-free Solovay-Kitaev theorem. In addition, for the first time, we demonstrate how to leverage RL-based quantum compilers to accomplish two-qubit operator compiling. The achieved results open an avenue for integrating RL with quantum compiling to unify efficiency and practicality and thus facilitate the exploration of quantum advantages.

Approximation bounds for norm constrained neural networks with applications to regression and GANs

This paper studies the approximation capacity of ReLU neural networks with norm constraint on the weights. We prove upper and lower bounds on the approximation error of these networks for smooth function classes. The lower bound is derived through the Rademacher complexity of neural networks, which may be of independent interest. We apply these approximation bounds to analyze the convergence of regression using norm constrained neural networks and distribution estimation by GANs. In particular, we obtain convergence rates for over-parameterized neural networks. It is also shown that GANs can achieve optimal rate of learning probability distributions, when the discriminator is a properly chosen norm constrained neural network.

Wasserstein Generative Learning of Conditional Distribution

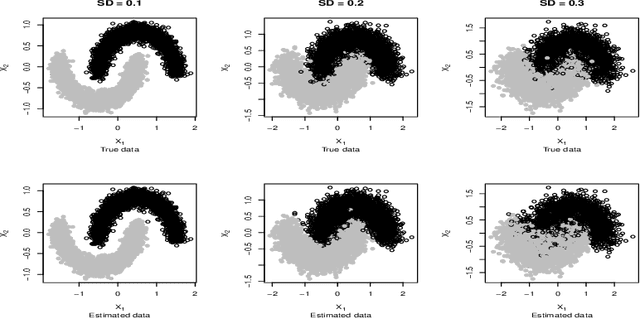
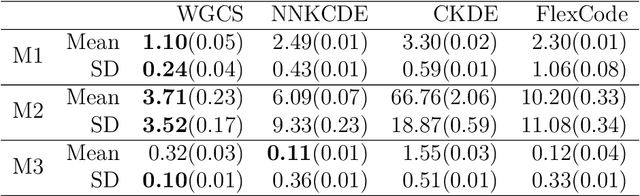
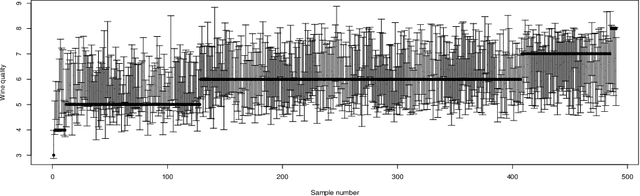
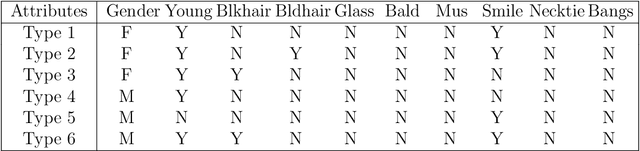
Conditional distribution is a fundamental quantity for describing the relationship between a response and a predictor. We propose a Wasserstein generative approach to learning a conditional distribution. The proposed approach uses a conditional generator to transform a known distribution to the target conditional distribution. The conditional generator is estimated by matching a joint distribution involving the conditional generator and the target joint distribution, using the Wasserstein distance as the discrepancy measure for these joint distributions. We establish non-asymptotic error bound of the conditional sampling distribution generated by the proposed method and show that it is able to mitigate the curse of dimensionality, assuming that the data distribution is supported on a lower-dimensional set. We conduct numerical experiments to validate proposed method and illustrate its applications to conditional sample generation, nonparametric conditional density estimation, prediction uncertainty quantification, bivariate response data, image reconstruction and image generation.