Yuejie Chi
SoteriaFL: A Unified Framework for Private Federated Learning with Communication Compression
Jun 20, 2022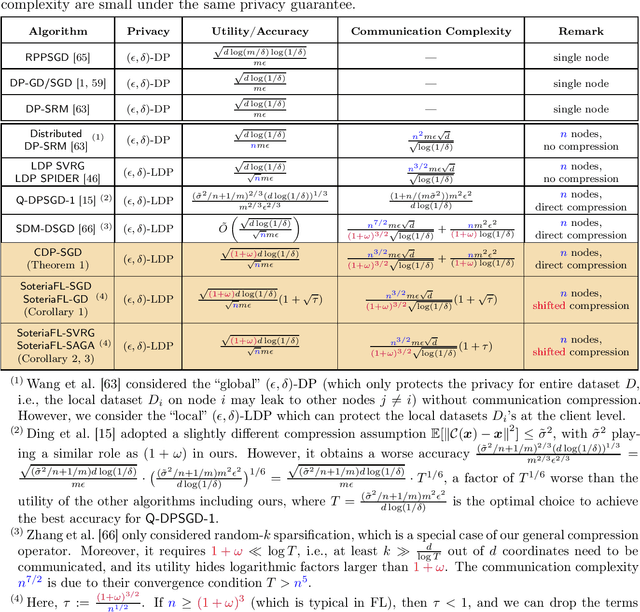

Abstract:To enable large-scale machine learning in bandwidth-hungry environments such as wireless networks, significant progress has been made recently in designing communication-efficient federated learning algorithms with the aid of communication compression. On the other end, privacy-preserving, especially at the client level, is another important desideratum that has not been addressed simultaneously in the presence of advanced communication compression techniques yet. In this paper, we propose a unified framework that enhances the communication efficiency of private federated learning with communication compression. Exploiting both general compression operators and local differential privacy, we first examine a simple algorithm that applies compression directly to differentially-private stochastic gradient descent, and identify its limitations. We then propose a unified framework SoteriaFL for private federated learning, which accommodates a general family of local gradient estimators including popular stochastic variance-reduced gradient methods and the state-of-the-art shifted compression scheme. We provide a comprehensive characterization of its performance trade-offs in terms of privacy, utility, and communication complexity, where SoteraFL is shown to achieve better communication complexity without sacrificing privacy nor utility than other private federated learning algorithms without communication compression.
Fast and Provable Tensor Robust Principal Component Analysis via Scaled Gradient Descent
Jun 18, 2022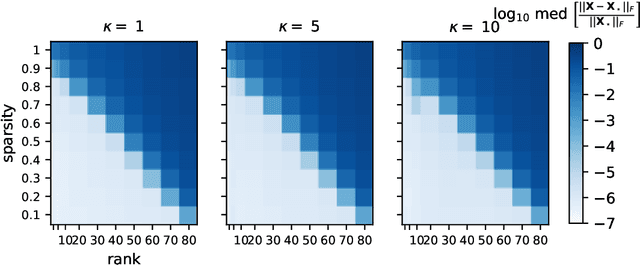


Abstract:An increasing number of data science and machine learning problems rely on computation with tensors, which better capture the multi-way relationships and interactions of data than matrices. When tapping into this critical advantage, a key challenge is to develop computationally efficient and provably correct algorithms for extracting useful information from tensor data that are simultaneously robust to corruptions and ill-conditioning. This paper tackles tensor robust principal component analysis (RPCA), which aims to recover a low-rank tensor from its observations contaminated by sparse corruptions, under the Tucker decomposition. To minimize the computation and memory footprints, we propose to directly recover the low-dimensional tensor factors -- starting from a tailored spectral initialization -- via scaled gradient descent (ScaledGD), coupled with an iteration-varying thresholding operation to adaptively remove the impact of corruptions. Theoretically, we establish that the proposed algorithm converges linearly to the true low-rank tensor at a constant rate that is independent with its condition number, as long as the level of corruptions is not too large. Empirically, we demonstrate that the proposed algorithm achieves better and more scalable performance than state-of-the-art matrix and tensor RPCA algorithms through synthetic experiments and real-world applications.
Independent Natural Policy Gradient Methods for Potential Games: Finite-time Global Convergence with Entropy Regularization
Apr 12, 2022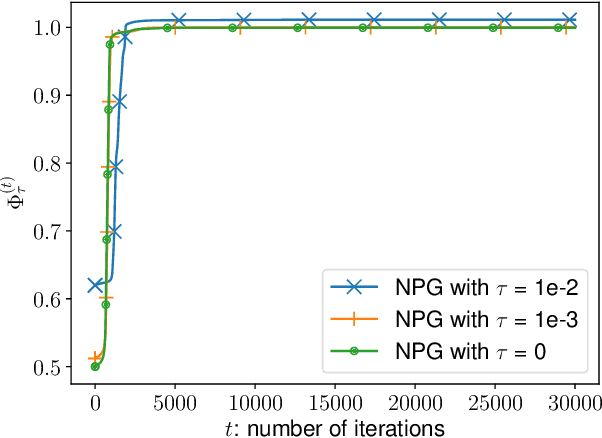
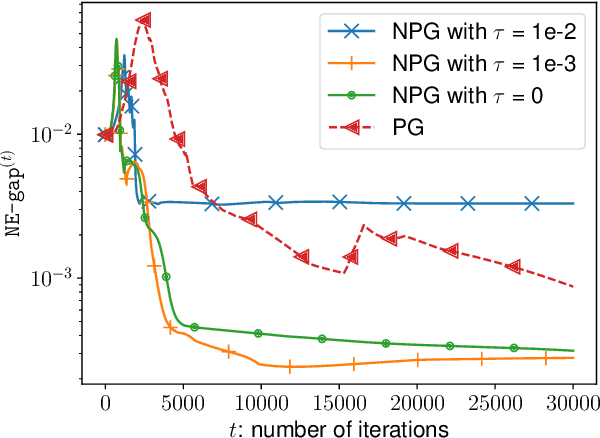
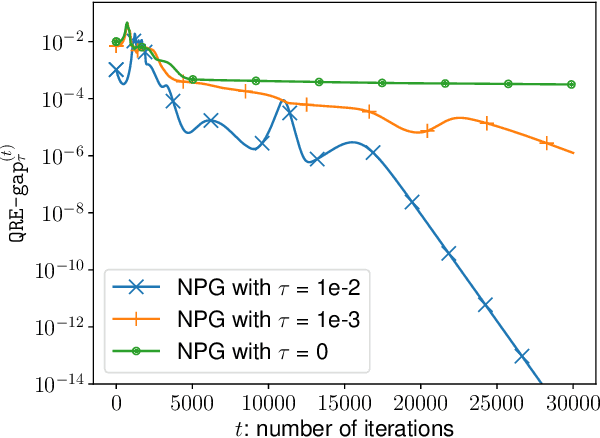
Abstract:A major challenge in multi-agent systems is that the system complexity grows dramatically with the number of agents as well as the size of their action spaces, which is typical in real world scenarios such as autonomous vehicles, robotic teams, network routing, etc. It is hence in imminent need to design decentralized or independent algorithms where the update of each agent is only based on their local observations without the need of introducing complex communication/coordination mechanisms. In this work, we study the finite-time convergence of independent entropy-regularized natural policy gradient (NPG) methods for potential games, where the difference in an agent's utility function due to unilateral deviation matches exactly that of a common potential function. The proposed entropy-regularized NPG method enables each agent to deploy symmetric, decentralized, and multiplicative updates according to its own payoff. We show that the proposed method converges to the quantal response equilibrium (QRE) -- the equilibrium to the entropy-regularized game -- at a sublinear rate, which is independent of the size of the action space and grows at most sublinearly with the number of agents. Appealingly, the convergence rate further becomes independent with the number of agents for the important special case of identical-interest games, leading to the first method that converges at a dimension-free rate. Our approach can be used as a smoothing technique to find an approximate Nash equilibrium (NE) of the unregularized problem without assuming that stationary policies are isolated.
Settling the Sample Complexity of Model-Based Offline Reinforcement Learning
Apr 11, 2022
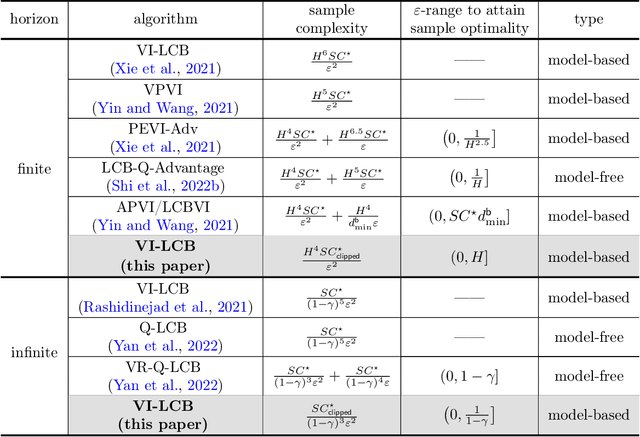
Abstract:This paper is concerned with offline reinforcement learning (RL), which learns using pre-collected data without further exploration. Effective offline RL would be able to accommodate distribution shift and limited data coverage. However, prior algorithms or analyses either suffer from suboptimal sample complexities or incur high burn-in cost to reach sample optimality, thus posing an impediment to efficient offline RL in sample-starved applications. We demonstrate that the model-based (or "plug-in") approach achieves minimax-optimal sample complexity without burn-in cost for tabular Markov decision processes (MDPs). Concretely, consider a finite-horizon (resp. $\gamma$-discounted infinite-horizon) MDP with $S$ states and horizon $H$ (resp. effective horizon $\frac{1}{1-\gamma}$), and suppose the distribution shift of data is reflected by some single-policy clipped concentrability coefficient $C^{\star}_{\text{clipped}}$. We prove that model-based offline RL yields $\varepsilon$-accuracy with a sample complexity of \[ \begin{cases} \frac{H^{4}SC_{\text{clipped}}^{\star}}{\varepsilon^{2}} & (\text{finite-horizon MDPs}) \frac{SC_{\text{clipped}}^{\star}}{(1-\gamma)^{3}\varepsilon^{2}} & (\text{infinite-horizon MDPs}) \end{cases} \] up to log factor, which is minimax optimal for the entire $\varepsilon$-range. Our algorithms are "pessimistic" variants of value iteration with Bernstein-style penalties, and do not require sophisticated variance reduction.
Pessimistic Q-Learning for Offline Reinforcement Learning: Towards Optimal Sample Complexity
Feb 28, 2022

Abstract:Offline or batch reinforcement learning seeks to learn a near-optimal policy using history data without active exploration of the environment. To counter the insufficient coverage and sample scarcity of many offline datasets, the principle of pessimism has been recently introduced to mitigate high bias of the estimated values. While pessimistic variants of model-based algorithms (e.g., value iteration with lower confidence bounds) have been theoretically investigated, their model-free counterparts -- which do not require explicit model estimation -- have not been adequately studied, especially in terms of sample efficiency. To address this inadequacy, we study a pessimistic variant of Q-learning in the context of finite-horizon Markov decision processes, and characterize its sample complexity under the single-policy concentrability assumption which does not require the full coverage of the state-action space. In addition, a variance-reduced pessimistic Q-learning algorithm is proposed to achieve near-optimal sample complexity. Altogether, this work highlights the efficiency of model-free algorithms in offline RL when used in conjunction with pessimism and variance reduction.
BEER: Fast $O$ Rate for Decentralized Nonconvex Optimization with Communication Compression
Jan 31, 2022
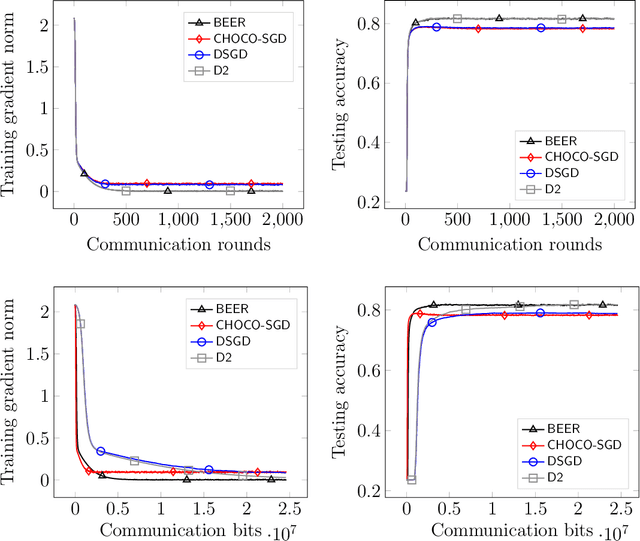
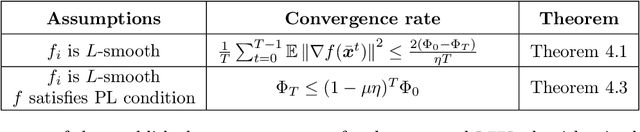
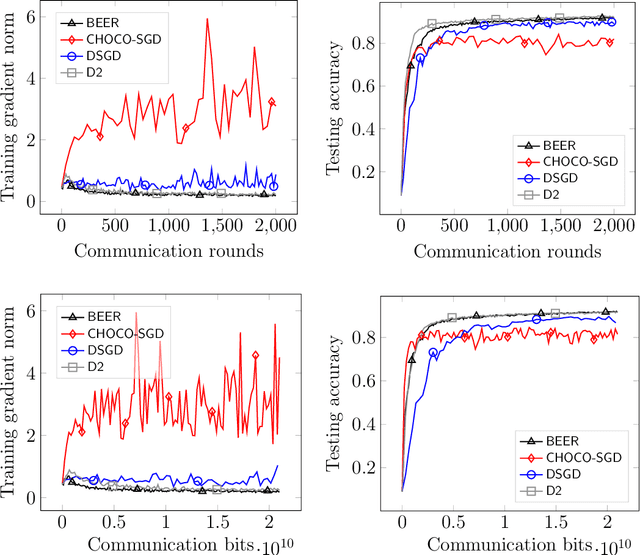
Abstract:Communication efficiency has been widely recognized as the bottleneck for large-scale decentralized machine learning applications in multi-agent or federated environments. To tackle the communication bottleneck, there have been many efforts to design communication-compressed algorithms for decentralized nonconvex optimization, where the clients are only allowed to communicate a small amount of quantized information (aka bits) with their neighbors over a predefined graph topology. Despite significant efforts, the state-of-the-art algorithm in the nonconvex setting still suffers from a slower rate of convergence $O((G/T)^{2/3})$ compared with their uncompressed counterpart, where $G$ measures the data heterogeneity across different clients, and $T$ is the number of communication rounds. This paper proposes BEER, which adopts communication compression with gradient tracking, and shows it converges at a faster rate of $O(1/T)$. This significantly improves over the state-of-the-art rate, by matching the rate without compression even under arbitrary data heterogeneity. Numerical experiments are also provided to corroborate our theory and confirm the practical superiority of BEER in the data heterogeneous regime.
Breaking the Sample Complexity Barrier to Regret-Optimal Model-Free Reinforcement Learning
Oct 09, 2021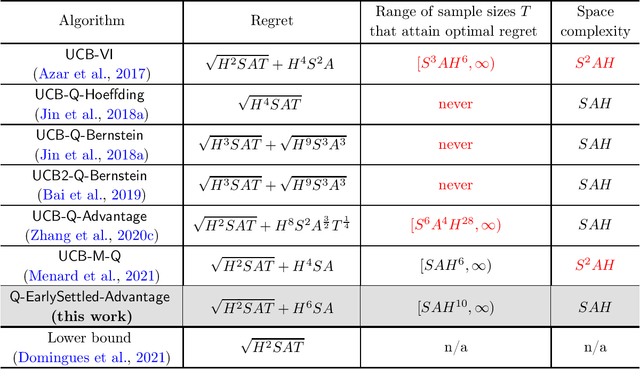
Abstract:Achieving sample efficiency in online episodic reinforcement learning (RL) requires optimally balancing exploration and exploitation. When it comes to a finite-horizon episodic Markov decision process with $S$ states, $A$ actions and horizon length $H$, substantial progress has been achieved towards characterizing the minimax-optimal regret, which scales on the order of $\sqrt{H^2SAT}$ (modulo log factors) with $T$ the total number of samples. While several competing solution paradigms have been proposed to minimize regret, they are either memory-inefficient, or fall short of optimality unless the sample size exceeds an enormous threshold (e.g., $S^6A^4 \,\mathrm{poly}(H)$ for existing model-free methods). To overcome such a large sample size barrier to efficient RL, we design a novel model-free algorithm, with space complexity $O(SAH)$, that achieves near-optimal regret as soon as the sample size exceeds the order of $SA\,\mathrm{poly}(H)$. In terms of this sample size requirement (also referred to the initial burn-in cost), our method improves -- by at least a factor of $S^5A^3$ -- upon any prior memory-efficient algorithm that is asymptotically regret-optimal. Leveraging the recently introduced variance reduction strategy (also called {\em reference-advantage decomposition}), the proposed algorithm employs an {\em early-settled} reference update rule, with the aid of two Q-learning sequences with upper and lower confidence bounds. The design principle of our early-settled variance reduction method might be of independent interest to other RL settings that involve intricate exploration-exploitation trade-offs.
DESTRESS: Computation-Optimal and Communication-Efficient Decentralized Nonconvex Finite-Sum Optimization
Oct 04, 2021



Abstract:Emerging applications in multi-agent environments such as internet-of-things, networked sensing, autonomous systems and federated learning, call for decentralized algorithms for finite-sum optimizations that are resource-efficient in terms of both computation and communication. In this paper, we consider the prototypical setting where the agents work collaboratively to minimize the sum of local loss functions by only communicating with their neighbors over a predetermined network topology. We develop a new algorithm, called DEcentralized STochastic REcurSive gradient methodS (DESTRESS) for nonconvex finite-sum optimization, which matches the optimal incremental first-order oracle (IFO) complexity of centralized algorithms for finding first-order stationary points, while maintaining communication efficiency. Detailed theoretical and numerical comparisons corroborate that the resource efficiencies of DESTRESS improve upon prior decentralized algorithms over a wide range of parameter regimes. DESTRESS leverages several key algorithm design ideas including stochastic recursive gradient updates with mini-batches for local computation, gradient tracking with extra mixing (i.e., multiple gossiping rounds) for per-iteration communication, together with careful choices of hyper-parameters and new analysis frameworks to provably achieve a desirable computation-communication trade-off.
Fast Policy Extragradient Methods for Competitive Games with Entropy Regularization
May 31, 2021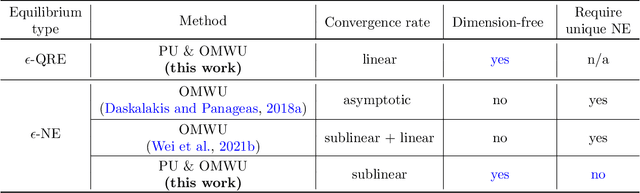
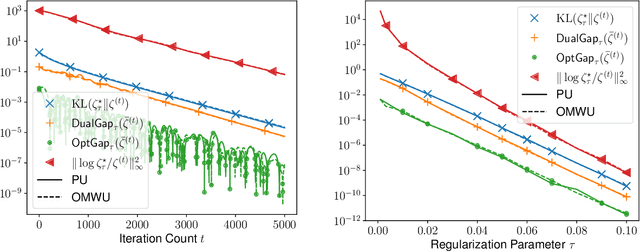
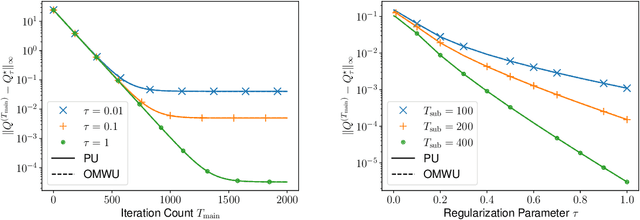
Abstract:This paper investigates the problem of computing the equilibrium of competitive games, which is often modeled as a constrained saddle-point optimization problem with probability simplex constraints. Despite recent efforts in understanding the last-iterate convergence of extragradient methods in the unconstrained setting, the theoretical underpinnings of these methods in the constrained settings, especially those using multiplicative updates, remain highly inadequate, even when the objective function is bilinear. Motivated by the algorithmic role of entropy regularization in single-agent reinforcement learning and game theory, we develop provably efficient extragradient methods to find the quantal response equilibrium (QRE) -- which are solutions to zero-sum two-player matrix games with entropy regularization -- at a linear rate. The proposed algorithms can be implemented in a decentralized manner, where each player executes symmetric and multiplicative updates iteratively using its own payoff without observing the opponent's actions directly. In addition, by controlling the knob of entropy regularization, the proposed algorithms can locate an approximate Nash equilibrium of the unregularized matrix game at a sublinear rate without assuming the Nash equilibrium to be unique. Our methods also lead to efficient policy extragradient algorithms for solving entropy-regularized zero-sum Markov games at a linear rate. All of our convergence rates are nearly dimension-free, which are independent of the size of the state and action spaces up to logarithm factors, highlighting the positive role of entropy regularization for accelerating convergence.
Policy Mirror Descent for Regularized Reinforcement Learning: A Generalized Framework with Linear Convergence
May 24, 2021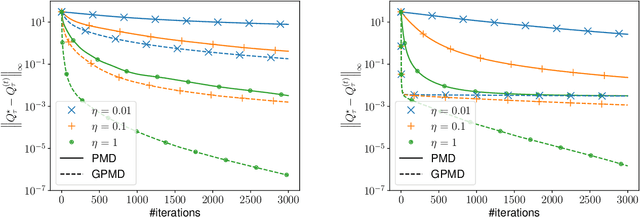
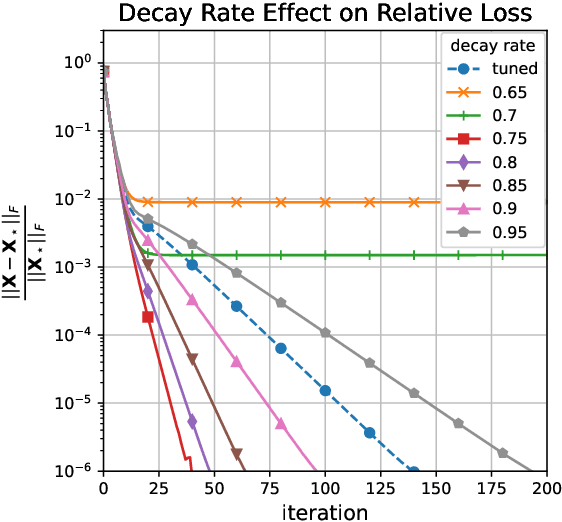
Abstract:Policy optimization, which learns the policy of interest by maximizing the value function via large-scale optimization techniques, lies at the heart of modern reinforcement learning (RL). In addition to value maximization, other practical considerations arise commonly as well, including the need of encouraging exploration, and that of ensuring certain structural properties of the learned policy due to safety, resource and operational constraints. These considerations can often be accounted for by resorting to regularized RL, which augments the target value function with a structure-promoting regularization term. Focusing on an infinite-horizon discounted Markov decision process, this paper proposes a generalized policy mirror descent (GPMD) algorithm for solving regularized RL. As a generalization of policy mirror descent Lan (2021), the proposed algorithm accommodates a general class of convex regularizers as well as a broad family of Bregman divergence in cognizant of the regularizer in use. We demonstrate that our algorithm converges linearly over an entire range of learning rates, in a dimension-free fashion, to the global solution, even when the regularizer lacks strong convexity and smoothness. In addition, this linear convergence feature is provably stable in the face of inexact policy evaluation and imperfect policy updates. Numerical experiments are provided to corroborate the applicability and appealing performance of GPMD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge