Learning with Complementary Labels Revisited: A Consistent Approach via Negative-Unlabeled Learning

Complementary-label learning is a weakly supervised learning problem in which each training example is associated with one or multiple complementary labels indicating the classes to which it does not belong. Existing consistent approaches have relied on the uniform distribution assumption to model the generation of complementary labels, or on an ordinary-label training set to estimate the transition matrix. However, both conditions may not be satisfied in real-world scenarios. In this paper, we propose a novel complementary-label learning approach that does not rely on these conditions. We find that complementary-label learning can be expressed as a set of negative-unlabeled binary classification problems when using the one-versus-rest strategy. This observation allows us to propose a risk-consistent approach with theoretical guarantees. Furthermore, we introduce a risk correction approach to address overfitting problems when using complex models. We also prove the statistical consistency and convergence rate of the corrected risk estimator. Extensive experimental results on both synthetic and real-world benchmark datasets validate the superiority of our proposed approach over state-of-the-art methods.

Adapting to Continuous Covariate Shift via Online Density Ratio Estimation

Dealing with distribution shifts is one of the central challenges for modern machine learning. One fundamental situation is the \emph{covariate shift}, where the input distributions of data change from training to testing stages while the input-conditional output distribution remains unchanged. In this paper, we initiate the study of a more challenging scenario -- \emph{continuous} covariate shift -- in which the test data appear sequentially, and their distributions can shift continuously. Our goal is to adaptively train the predictor such that its prediction risk accumulated over time can be minimized. Starting with the importance-weighted learning, we show the method works effectively if the time-varying density ratios of test and train inputs can be accurately estimated. However, existing density ratio estimation methods would fail due to data scarcity at each time step. To this end, we propose an online method that can appropriately reuse historical information. Our density ratio estimation method is proven to perform well by enjoying a dynamic regret bound, which finally leads to an excess risk guarantee for the predictor. Empirical results also validate the effectiveness.

Adapting to Online Label Shift with Provable Guarantees

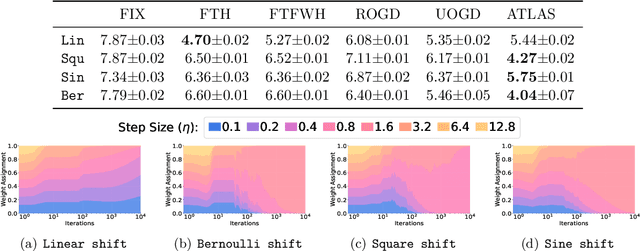
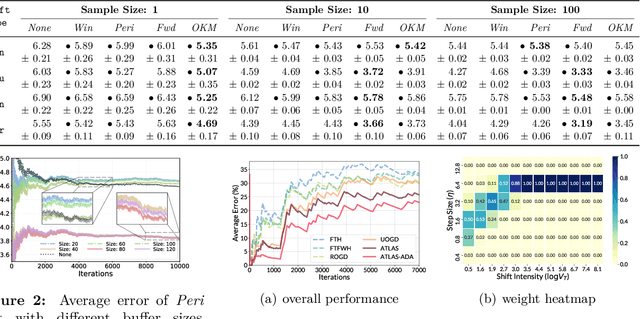
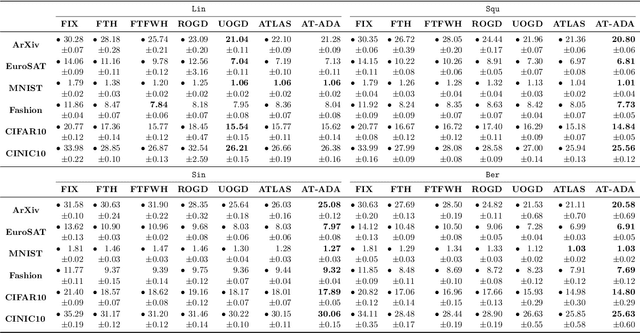
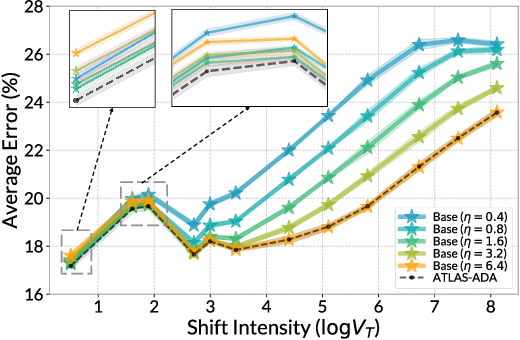
The standard supervised learning paradigm works effectively when training data shares the same distribution as the upcoming testing samples. However, this assumption is often violated in real-world applications, especially when testing data appear in an online fashion. In this paper, we formulate and investigate the problem of online label shift (OLaS): the learner trains an initial model from the labeled offline data and then deploys it to an unlabeled online environment where the underlying label distribution changes over time but the label-conditional density does not. The non-stationarity nature and the lack of supervision make the problem challenging to be tackled. To address the difficulty, we construct a new unbiased risk estimator that utilizes the unlabeled data, which exhibits many benign properties albeit with potential non-convexity. Building upon that, we propose novel online ensemble algorithms to deal with the non-stationarity of the environments. Our approach enjoys optimal dynamic regret, indicating that the performance is competitive with a clairvoyant who knows the online environments in hindsight and then chooses the best decision for each round. The obtained dynamic regret bound scales with the intensity and pattern of label distribution shift, hence exhibiting the adaptivity in the OLaS problem. Extensive experiments are conducted to validate the effectiveness and support our theoretical findings.

Adaptivity and Non-stationarity: Problem-dependent Dynamic Regret for Online Convex Optimization

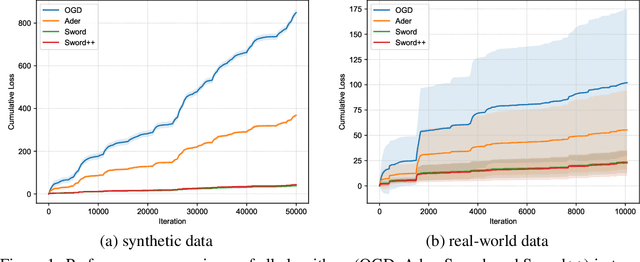
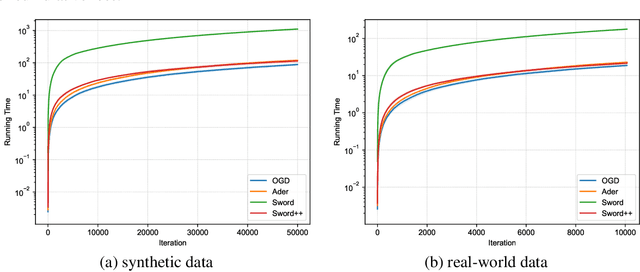
We investigate online convex optimization in non-stationary environments and choose the \emph{dynamic regret} as the performance measure, defined as the difference between cumulative loss incurred by the online algorithm and that of any feasible comparator sequence. Let $T$ be the time horizon and $P_T$ be the path-length that essentially reflects the non-stationarity of environments, the state-of-the-art dynamic regret is $\mathcal{O}(\sqrt{T(1+P_T)})$. Although this bound is proved to be minimax optimal for convex functions, in this paper, we demonstrate that it is possible to further enhance the guarantee for some easy problem instances, particularly when online functions are smooth. Specifically, we propose novel online algorithms that can leverage smoothness and replace the dependence on $T$ in the dynamic regret by \emph{problem-dependent} quantities: the variation in gradients of loss functions, the cumulative loss of the comparator sequence, and the minimum of the previous two terms. These quantities are at most $\mathcal{O}(T)$ while could be much smaller in benign environments. Therefore, our results are adaptive to the intrinsic difficulty of the problem, since the bounds are tighter than existing results for easy problems and meanwhile guarantee the same rate in the worst case. Notably, our algorithm requires only \emph{one} gradient per iteration, which shares the same gradient query complexity with the methods developed for optimizing the static regret. As a further application, we extend the results from the full-information setting to bandit convex optimization with two-point feedback and thereby attain the first problem-dependent dynamic regret for such bandit tasks.

Dynamic Regret of Convex and Smooth Functions

We investigate online convex optimization in non-stationary environments and choose the dynamic regret as the performance measure, defined as the difference between cumulative loss incurred by the online algorithm and that of any feasible comparator sequence. Let $T$ be the time horizon and $P_T$ be the path-length that essentially reflects the non-stationarity of environments, the state-of-the-art dynamic regret is $\mathcal{O}(\sqrt{T(1+P_T)})$. Although this bound is proved to be minimax optimal for convex functions, in this paper, we demonstrate that it is possible to further enhance the dynamic regret by exploiting the smoothness condition. Specifically, we propose novel online algorithms that are capable of leveraging smoothness and replace the dependence on $T$ in the dynamic regret by problem-dependent quantities: the variation in gradients of loss functions, and the cumulative loss of the comparator sequence. These quantities are at most $\mathcal{O}(T)$ while could be much smaller in benign environments. Therefore, our results are adaptive to the intrinsic difficulty of the problem, since the bounds are tighter than existing results for easy problems and meanwhile guarantee the same rate in the worst case.

Exploratory Machine Learning with Unknown Unknowns

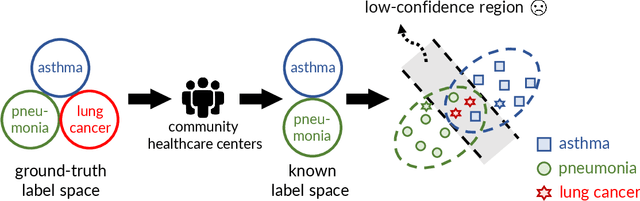
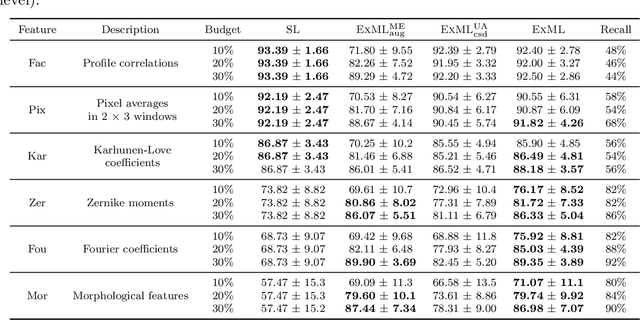
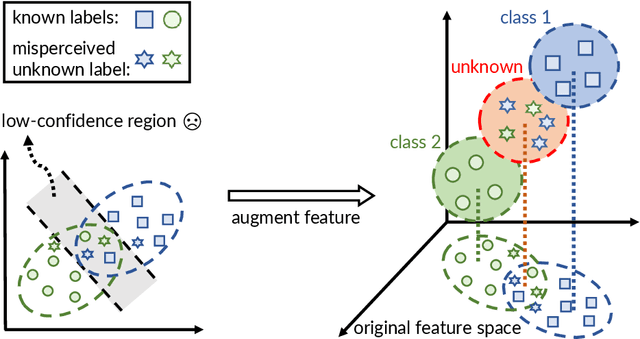
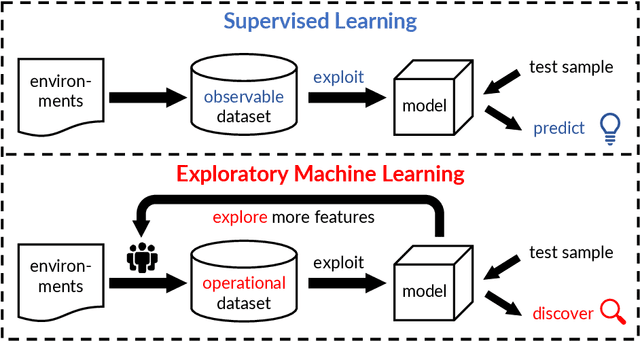
In conventional supervised learning, a training dataset is given with ground-truth labels from a known label set, and the learned model will classify unseen instances to the known labels. In this paper, we study a new problem setting in which there are unknown classes in the training dataset misperceived as other labels, and thus their existence appears unknown from the given supervision. We attribute the unknown unknowns to the fact that the training dataset is badly advised by the incompletely perceived label space due to the insufficient feature information. To this end, we propose the exploratory machine learning, which examines and investigates the training dataset by actively augmenting the feature space to discover potentially unknown labels. Our approach consists of three ingredients including rejection model, feature acquisition, and model cascade. The effectiveness is validated on both synthetic and real datasets.

An Unbiased Risk Estimator for Learning with Augmented Classes

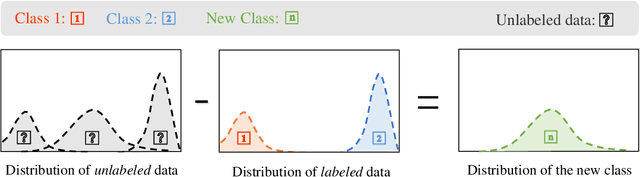
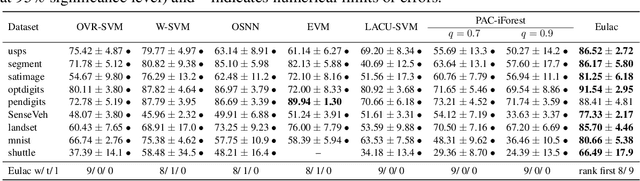
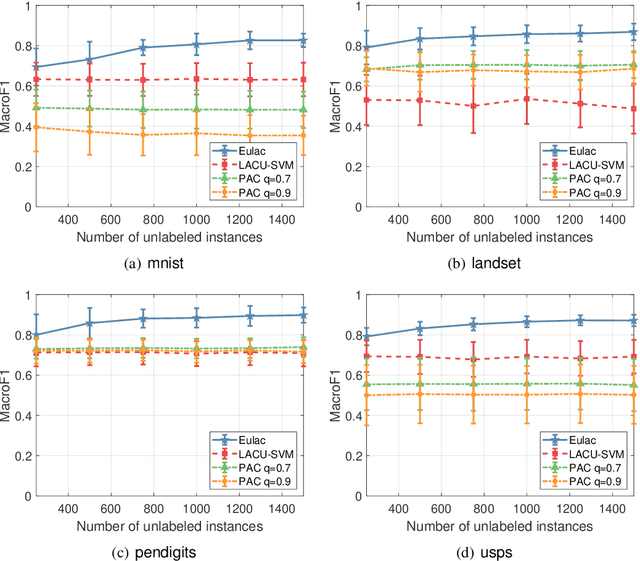
In this paper, we study the problem of learning with augmented classes (LAC), where new classes that do not appear in the training dataset might emerge in the testing phase. The mixture of known classes and new classes in the testing distribution makes the LAC problem quite challenging. Our discovery is that by exploiting cheap and vast unlabeled data, the testing distribution can be estimated in the training stage, which paves us a way to develop algorithms with nice statistical properties. Specifically, we propose an unbiased risk estimator over the testing distribution for the LAC problem, and further develop an efficient algorithm to perform the empirical risk minimization. Both asymptotic and non-asymptotic analyses are provided as theoretical guarantees. The efficacy of the proposed algorithm is also confirmed by experiments.