Learning Stochastic Dynamics with Statistics-Informed Neural Network

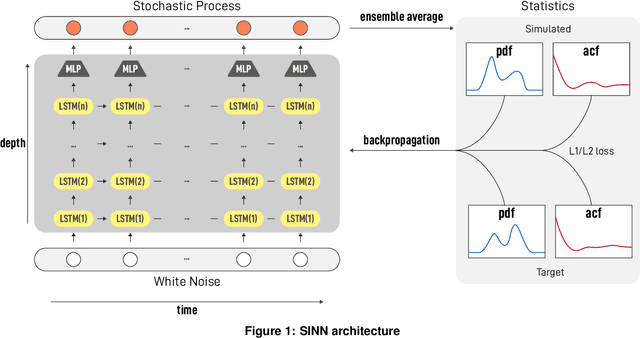
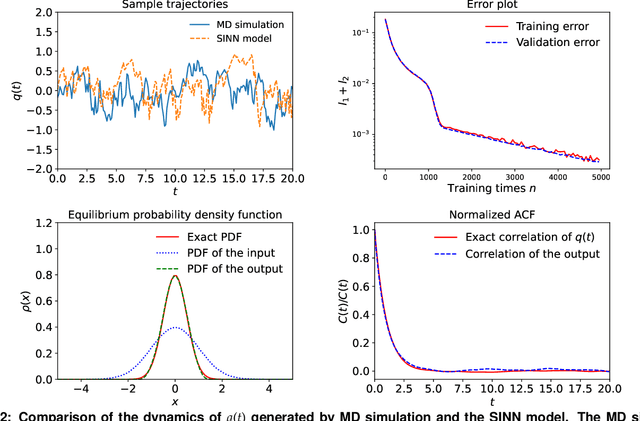
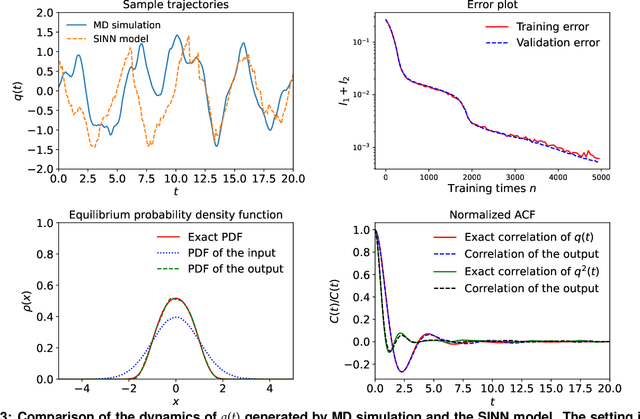
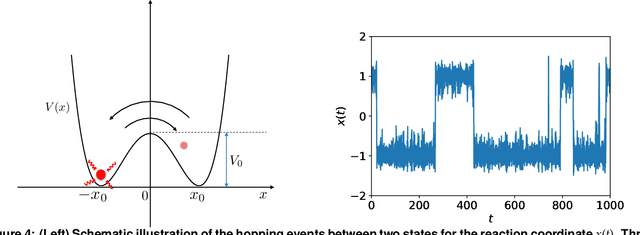
We introduce a machine-learning framework named statistics-informed neural network (SINN) for learning stochastic dynamics from data. This new architecture was theoretically inspired by a universal approximation theorem for stochastic systems introduced in this paper and the projection-operator formalism for stochastic modeling. We devise mechanisms for training the neural network model to reproduce the correct \emph{statistical} behavior of a target stochastic process. Numerical simulation results demonstrate that a well-trained SINN can reliably approximate both Markovian and non-Markovian stochastic dynamics. We demonstrate the applicability of SINN to model transition dynamics. Furthermore, we show that the obtained reduced-order model can be trained on temporally coarse-grained data and hence is well suited for rare-event simulations.

Nonlinear Matrix Approximation with Radial Basis Function Components

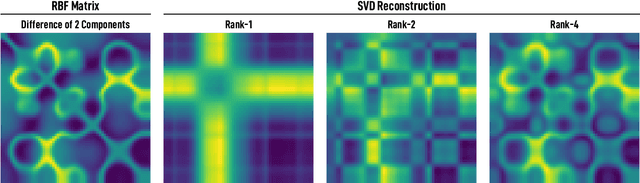
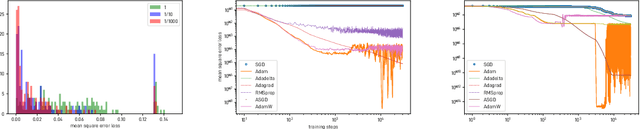
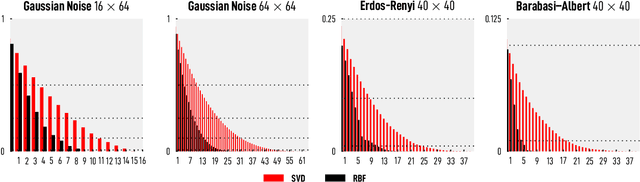
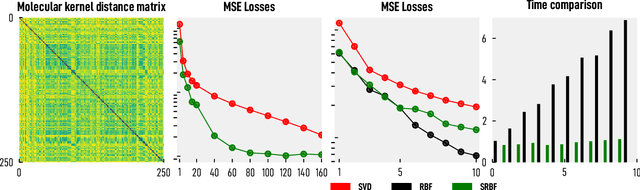
We introduce and investigate matrix approximation by decomposition into a sum of radial basis function (RBF) components. An RBF component is a generalization of the outer product between a pair of vectors, where an RBF function replaces the scalar multiplication between individual vector elements. Even though the RBF functions are positive definite, the summation across components is not restricted to convex combinations and allows us to compute the decomposition for any real matrix that is not necessarily symmetric or positive definite. We formulate the problem of seeking such a decomposition as an optimization problem with a nonlinear and non-convex loss function. Several modern versions of the gradient descent method, including their scalable stochastic counterparts, are used to solve this problem. We provide extensive empirical evidence of the effectiveness of the RBF decomposition and that of the gradient-based fitting algorithm. While being conceptually motivated by singular value decomposition (SVD), our proposed nonlinear counterpart outperforms SVD by drastically reducing the memory required to approximate a data matrix with the same L2 error for a wide range of matrix types. For example, it leads to 2 to 6 times memory save for Gaussian noise, graph adjacency matrices, and kernel matrices. Moreover, this proximity-based decomposition can offer additional interpretability in applications that involve, e.g., capturing the inner low-dimensional structure of the data, retaining graph connectivity structure, and preserving the acutance of images.

Graphical Gaussian Process Regression Model for Aqueous Solvation Free Energy Prediction of Organic Molecules in Redox Flow Battery

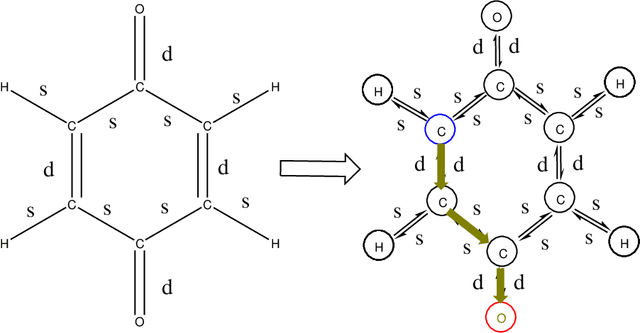
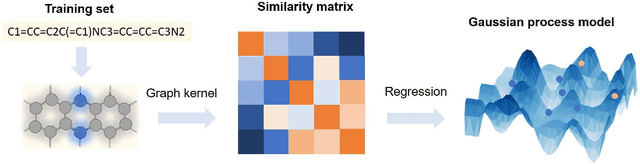
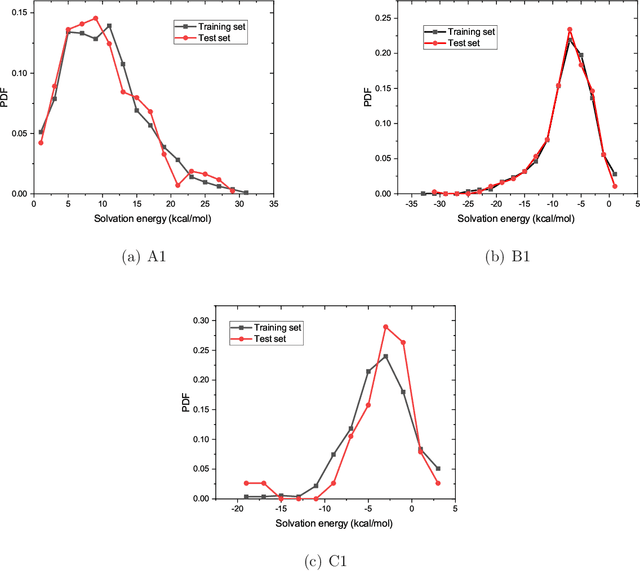
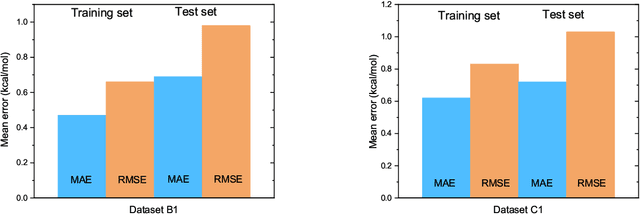
The solvation free energy of organic molecules is a critical parameter in determining emergent properties such as solubility, liquid-phase equilibrium constants, and pKa and redox potentials in an organic redox flow battery. In this work, we present a machine learning (ML) model that can learn and predict the aqueous solvation free energy of an organic molecule using Gaussian process regression method based on a new molecular graph kernel. To investigate the performance of the ML model on electrostatic interaction, the nonpolar interaction contribution of solvent and the conformational entropy of solute in solvation free energy, three data sets with implicit or explicit water solvent models, and contribution of conformational entropy of solute are tested. We demonstrate that our ML model can predict the solvation free energy of molecules at chemical accuracy with a mean absolute error of less than 1 kcal/mol for subsets of the QM9 dataset and the Freesolv database. To solve the general data scarcity problem for a graph-based ML model, we propose a dimension reduction algorithm based on the distance between molecular graphs, which can be used to examine the diversity of the molecular data set. It provides a promising way to build a minimum training set to improve prediction for certain test sets where the space of molecular structures is predetermined.

Detecting Label Noise via Leave-One-Out Cross-Validation

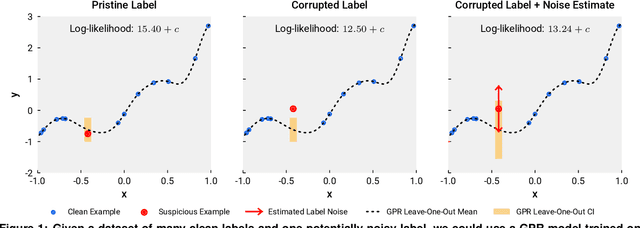
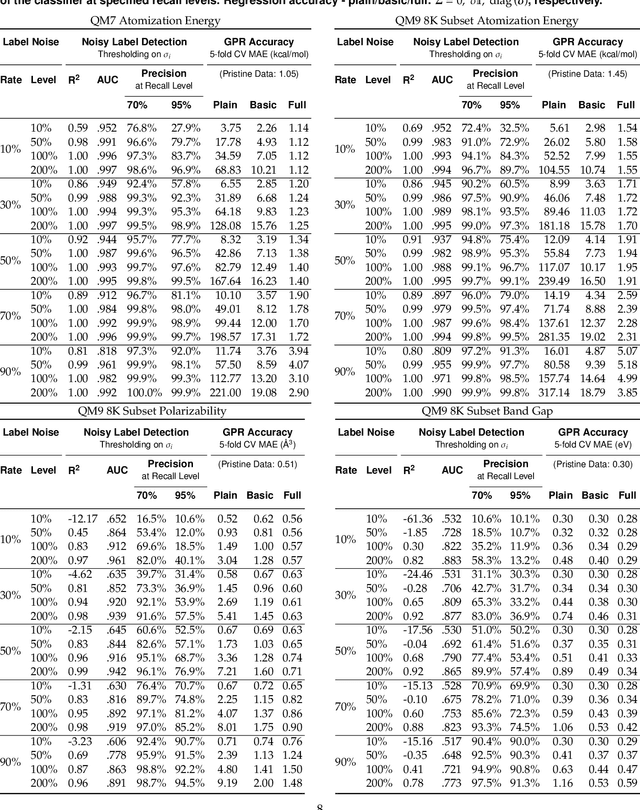
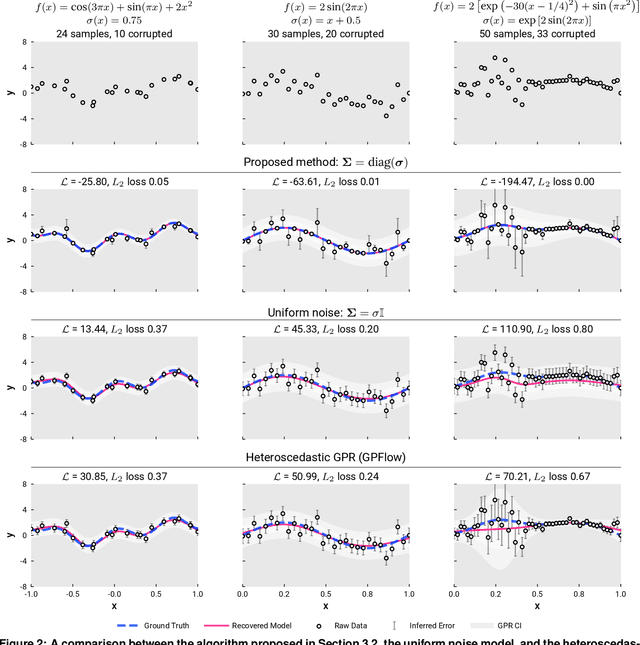
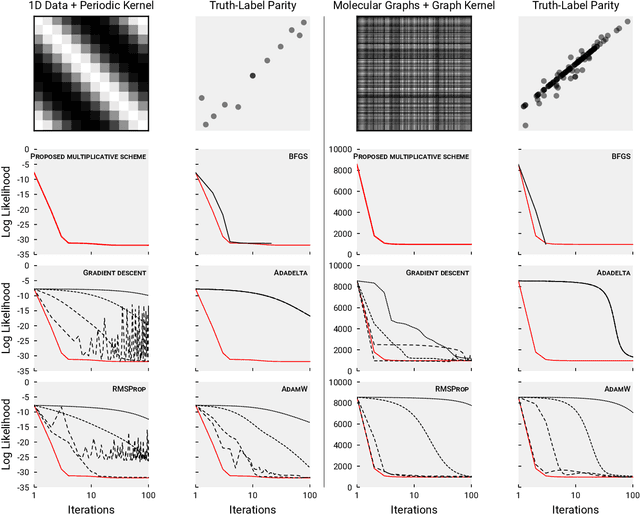
We present a simple algorithm for identifying and correcting real-valued noisy labels from a mixture of clean and corrupted sample points using Gaussian process regression. A heteroscedastic noise model is employed, in which additive Gaussian noise terms with independent variances are associated with each and all of the observed labels. Optimizing the noise model using maximum likelihood estimation leads to the containment of the GPR model's predictive error by the posterior standard deviation in leave-one-out cross-validation. A multiplicative update scheme is proposed for solving the maximum likelihood estimation problem under non-negative constraints. While we provide proof of convergence for certain special cases, the multiplicative scheme has empirically demonstrated monotonic convergence behavior in virtually all our numerical experiments. We show that the presented method can pinpoint corrupted sample points and lead to better regression models when trained on synthetic and real-world scientific data sets.

A High-Throughput Solver for Marginalized Graph Kernels on GPU

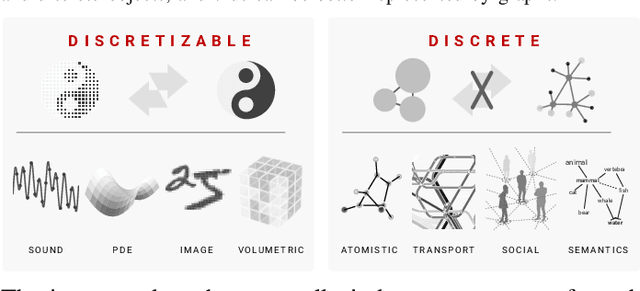
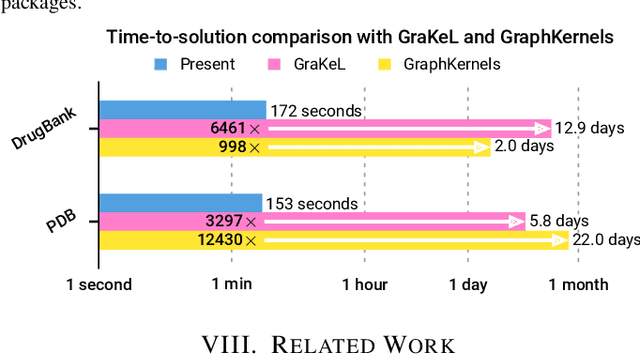
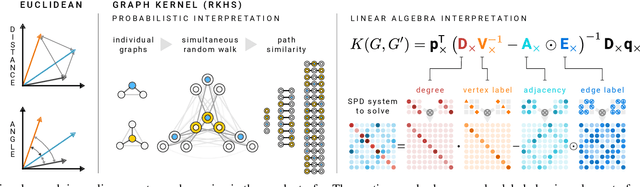
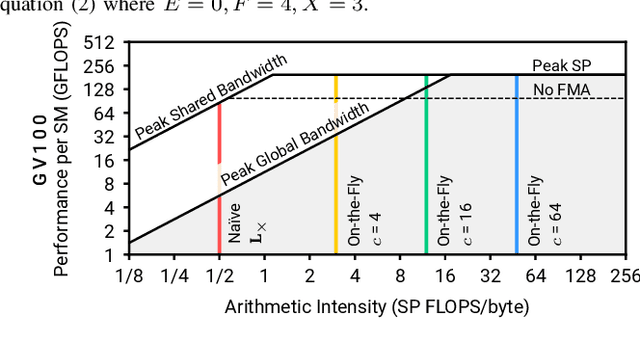
We present the design and optimization of a solver for efficient and high-throughput computation of the marginalized graph kernel on General Purpose GPUs. The graph kernel is computed using the conjugate gradient method to solve a generalized Laplacian of the tensor product between a pair of graphs. To cope with the large gap between the instruction throughput and the memory bandwidth of the GPUs, our solver forms the graph tensor product on-the-fly without storing it in memory. This is achieved by using threads in a warp cooperatively to stream the adjacency and edge label matrices of individual graphs by small square matrix blocks called tiles, which are then staged in registers and the shared memory for later reuse. Warps across a thread block can further share tiles via the shared memory to increase data reuse. We exploit the sparsity of the graphs hierarchically by storing only non-empty tiles using a coordinate format and nonzero elements within each tile using bitmaps. We propose a new partition-based reordering algorithm for aggregating nonzero elements of the graphs into fewer but denser tiles to further exploit sparsity. We carry out extensive theoretical analyses on the graph tensor product primitives for tiles of various density and evaluate their performance on synthetic and real-world datasets. Our solver delivers three to four orders of magnitude speedup over existing CPU-based solvers such as GraKeL and GraphKernels. The capability of the solver enables kernel-based learning tasks at unprecedented scales.

Prediction of Atomization Energy Using Graph Kernel and Active Learning

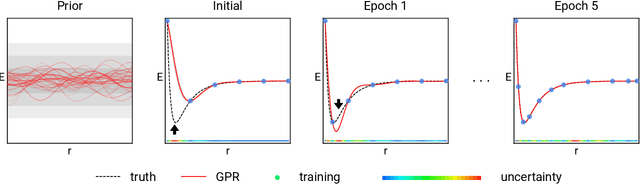
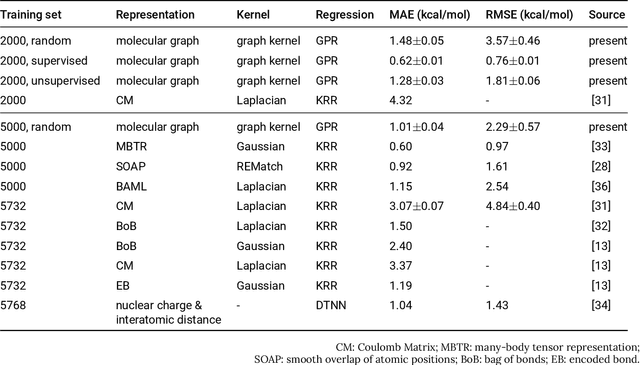
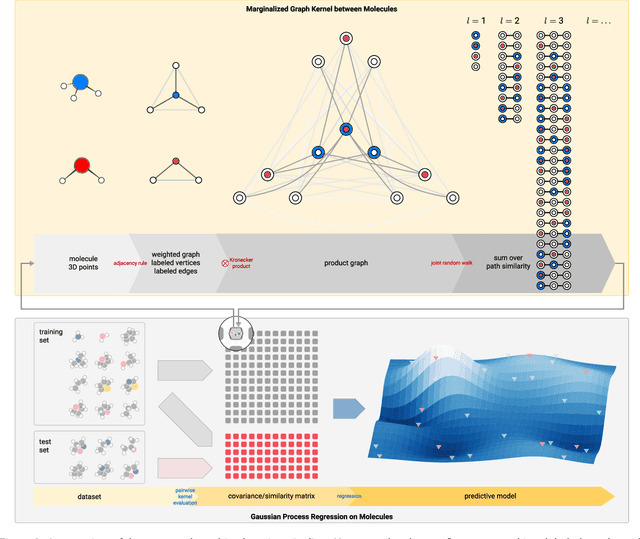
Data-driven prediction of molecular properties presents unique challenges to the design of machine learning methods concerning data structure/dimensionality, symmetry adaption, and confidence management. In this paper, we present a kernel-based pipeline that can learn and predict the atomization energy of molecules with high accuracy. The framework employs Gaussian process regression to perform predictions based on the similarity between molecules, which is computed using the marginalized graph kernel. We discuss why the graph kernel, paired with a graph representation of the molecules, is particularly useful for predicting extensive properties. We demonstrate that using an active learning procedure, the proposed method can achieve a mean absolute error less than 1.0 kcal/mol on the QM7 data set using as few as 1200 training samples and 1 hour of training time. This is a demonstration, in contrast to common believes, that regression models based on kernel methods can be simultaneously accurate and fast predictors.