Learning nonlinear integral operators via Recurrent Neural Networks and its application in solving Integro-Differential Equations

In this paper, we propose using LSTM-RNNs (Long Short-Term Memory-Recurrent Neural Networks) to learn and represent nonlinear integral operators that appear in nonlinear integro-differential equations (IDEs). The LSTM-RNN representation of the nonlinear integral operator allows us to turn a system of nonlinear integro-differential equations into a system of ordinary differential equations for which many efficient solvers are available. Furthermore, because the use of LSTM-RNN representation of the nonlinear integral operator in an IDE eliminates the need to perform a numerical integration in each numerical time evolution step, the overall temporal cost of the LSTM-RNN-based IDE solver can be reduced to $O(n_T)$ from $O(n_T^2)$ if a $n_T$-step trajectory is to be computed. We illustrate the efficiency and robustness of this LSTM-RNN-based numerical IDE solver with a model problem. Additionally, we highlight the generalizability of the learned integral operator by applying it to IDEs driven by different external forces. As a practical application, we show how this methodology can effectively solve the Dyson's equation for quantum many-body systems.

Probing reaction channels via reinforcement learning

We propose a reinforcement learning based method to identify important configurations that connect reactant and product states along chemical reaction paths. By shooting multiple trajectories from these configurations, we can generate an ensemble of configurations that concentrate on the transition path ensemble. This configuration ensemble can be effectively employed in a neural network-based partial differential equation solver to obtain an approximation solution of a restricted Backward Kolmogorov equation, even when the dimension of the problem is very high. The resulting solution, known as the committor function, encodes mechanistic information for the reaction and can in turn be used to evaluate reaction rates.

Learning Stochastic Dynamics with Statistics-Informed Neural Network

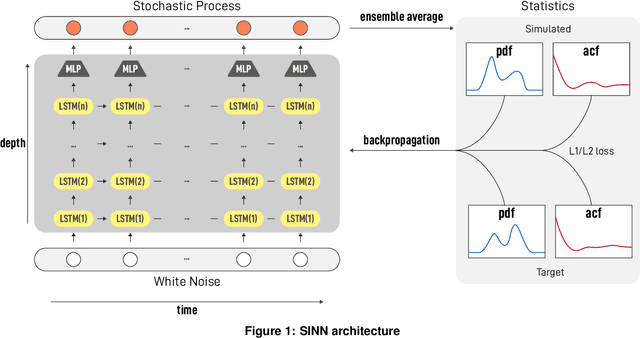
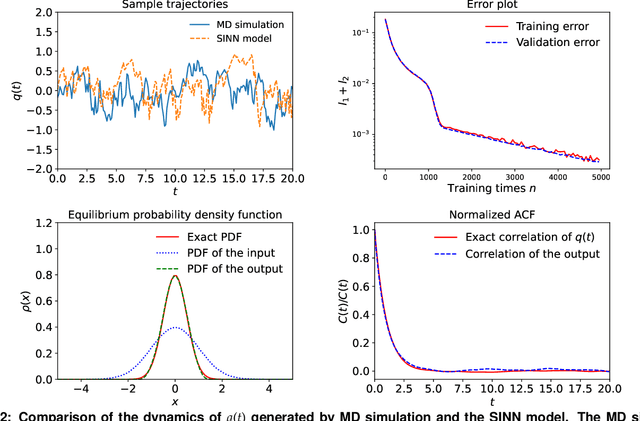
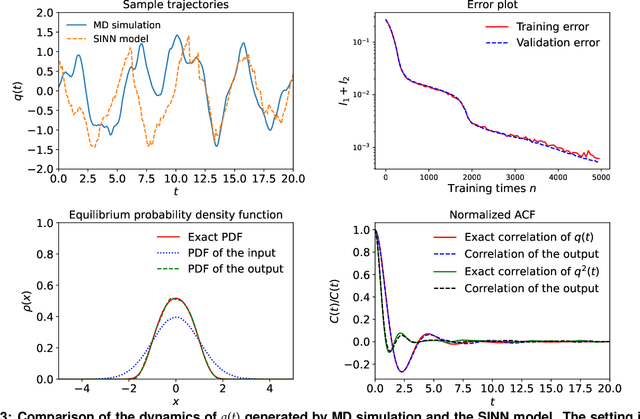
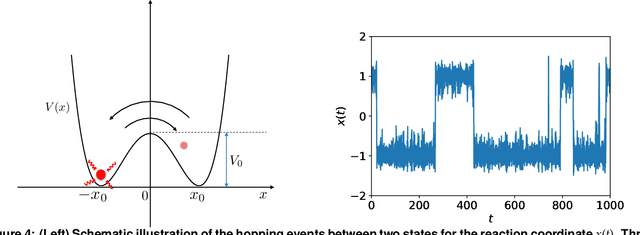
We introduce a machine-learning framework named statistics-informed neural network (SINN) for learning stochastic dynamics from data. This new architecture was theoretically inspired by a universal approximation theorem for stochastic systems introduced in this paper and the projection-operator formalism for stochastic modeling. We devise mechanisms for training the neural network model to reproduce the correct \emph{statistical} behavior of a target stochastic process. Numerical simulation results demonstrate that a well-trained SINN can reliably approximate both Markovian and non-Markovian stochastic dynamics. We demonstrate the applicability of SINN to model transition dynamics. Furthermore, we show that the obtained reduced-order model can be trained on temporally coarse-grained data and hence is well suited for rare-event simulations.

Detecting Label Noise via Leave-One-Out Cross-Validation

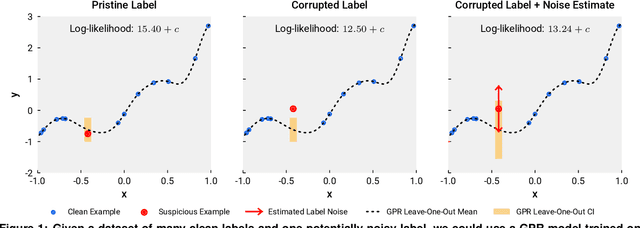
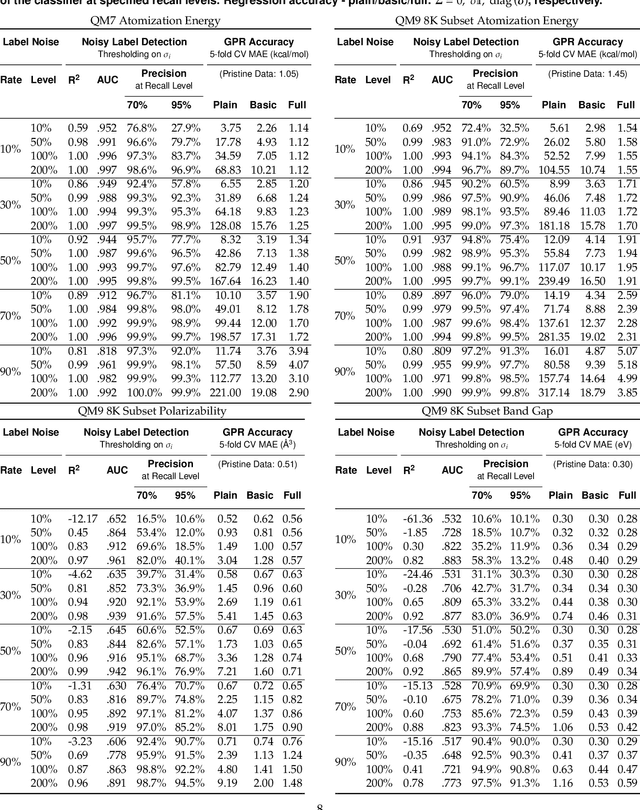
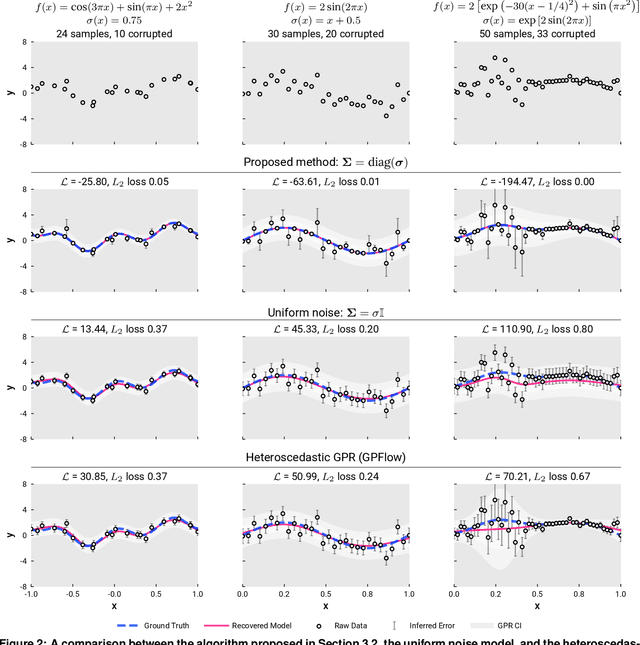
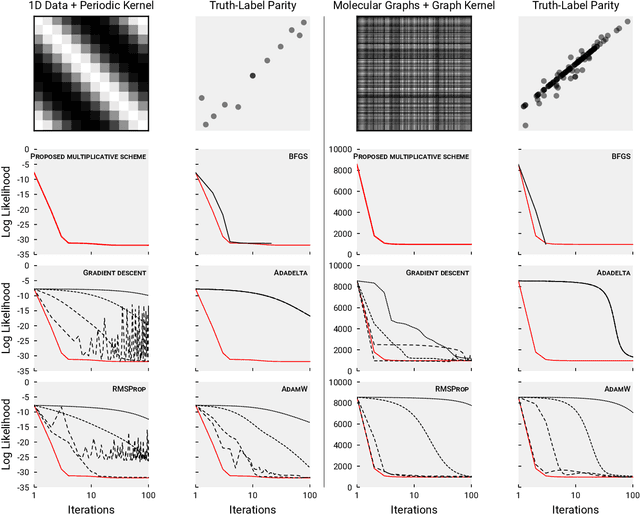
We present a simple algorithm for identifying and correcting real-valued noisy labels from a mixture of clean and corrupted sample points using Gaussian process regression. A heteroscedastic noise model is employed, in which additive Gaussian noise terms with independent variances are associated with each and all of the observed labels. Optimizing the noise model using maximum likelihood estimation leads to the containment of the GPR model's predictive error by the posterior standard deviation in leave-one-out cross-validation. A multiplicative update scheme is proposed for solving the maximum likelihood estimation problem under non-negative constraints. While we provide proof of convergence for certain special cases, the multiplicative scheme has empirically demonstrated monotonic convergence behavior in virtually all our numerical experiments. We show that the presented method can pinpoint corrupted sample points and lead to better regression models when trained on synthetic and real-world scientific data sets.